 Author
Author |
Topic: largest common subtree (Read 7593 times) |
|
pirate768
Newbie



Posts: 6
|
A subtree of a rooted, ordered binary tree T consists of a node and all its descendants. Write a method to determine the largest common subtree (structurally) of two given binary trees T1 and T2, that is, the largest subtree of T1 that is structurally identical to a subtree in T2. The contents of the nodes are irrelevant; we are only interested in matching the underlying structure of the trees.
|
|
 IP Logged IP Logged |
 |
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: largest common subtree
« Reply #1 on: Jun 29th, 2007, 3:11am » |
 Quote Quote  Modify Modify
|
You can reduce it to a largest common 'substring' problem.
|
|
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
pirate768
Newbie



Posts: 6
|
 |
Re: largest common subtree
« Reply #2 on: Jun 29th, 2007, 4:10am » |
 Quote Quote  Modify Modify
|
yeah u r right ...
but the fundtion signature is like this :
struct node{
int number;
node* left;
node* right;
};
node* find_largest_common_subtree (node* root1, node* root2)
i guess there is some simpler way ?
|
|
 IP Logged IP Logged |
|
|
|
labrin
Newbie


Posts: 9
|
 |
Re: largest common subtree
« Reply #3 on: Jun 29th, 2007, 7:40am » |
 Quote Quote  Modify Modify
|
from this signature also u can find as towr said:
node* find_largest_common_subtree (node* root1, node* root2)
{ 1. Do traversal ( say preorder) using stack and store 'L' and 'R' for left and right child in two arrays for two trees.
2. apply any std largest common substring algo.
}
|
|
 IP Logged IP Logged |
|
|
|
randome
Newbie


Posts: 6
|
 |
Re: largest common subtree
« Reply #4 on: Jul 13th, 2007, 11:18pm » |
 Quote Quote  Modify Modify
|
I think simple recursion can work here...
Code:
bool isEqualTree(root1, root2)
{
// base case: (we reach end of tree or are given two null nodes)
if(root1 ==NULL && root2 ==NULL) return true;
if(root1->left ==NULL && root2->left==NULL && root1->right ==NULL && root2->right==NULL)
return true;
if(!root1->left && root2->left || root1->left && !root2->left ) return false;
if(!root1->right && root2->right || root1->right && !root2->right ) return false;
return (isEqualTree(root1->right,root2->right) &&isEqualTree(root1->left,root2->left))
} |
|
|
| « Last Edit: Jul 13th, 2007, 11:20pm by randome » |
 IP Logged IP Logged |
|
|
|
sk
Newbie


Posts: 45
|
 |
Re: largest common subtree
« Reply #5 on: Sep 6th, 2007, 3:27pm » |
 Quote Quote  Modify Modify
|
simple recursion will incur more time.
the previous one works better.
convert the tree into a pre-order string reprsentation
e.g.
a simple tree with a 3 nodes can be imagined as
+
a b
can be reprsented as (+ab)
So the tree in the above example can be represented as
1st tree: +(+(+ab)b)(+(+a)+b)))
2nd tree: +(a)(+(+(+a)(b)))(+(+ab)b)
Note that +(+ab )b match.
to find this u can now use a prefix tree
|
| « Last Edit: Sep 6th, 2007, 3:28pm by sk » |
 IP Logged IP Logged |
|
|
|
wangzhen
Newbie


Posts: 21
|
 |
Re: largest common subtree
« Reply #6 on: Sep 6th, 2007, 9:37pm » |
 Quote Quote  Modify Modify
|
One option:
inorder tranverse the two trees, and calculate number of nodes in each subtree.
Sort these numbers in descending order.
only the subtrees with same numbers have the chance to match.
|
|
 IP Logged IP Logged |
|
|
|
goforit
Newbie


Posts: 5
|
 |
Re: largest common subtree
« Reply #7 on: Sep 8th, 2007, 12:32am » |
 Quote Quote  Modify Modify
|
What about doing a BFS and at each node checking for equal of the trees...
But each time find the size of the tree and always maintain the pointers for the largest subtree
|
| « Last Edit: Sep 8th, 2007, 12:39am by goforit » |
 IP Logged IP Logged |
|
|
|
johny_cage
Full Member
  

Gender: 
Posts: 155
|
 |
Re: largest common subtree
« Reply #8 on: Sep 26th, 2007, 6:07pm » |
 Quote Quote  Modify Modify
|
@randome
your recursive algorithm assumes both nodes to be at same level for structurally same. but in the example given by pirate768, structure can be same at different levels.
So, the condition u r checking i.e.
if(!root1->left && root2->left || root1->left && !root2->left ) return false;
has no useful meaning. Moreover it is wrong to say this. The contradict example is already provided by pirate786.
Correct me if I am wrong.
Thanks.....
|
|
 IP Logged IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: largest common subtree
« Reply #9 on: Sep 27th, 2007, 12:58am » |
 Quote Quote  Modify Modify
|
I think his code is only meant to do what the function name says: check that two (sub)trees are identical.
So to solve the problem he'd still have to traverse both trees, and then compare every subtree of one with those of the other one.
|
|
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
m_aakash
Junior Member
 

Posts: 96
|
 |
Re: largest common subtree
« Reply #10 on: Mar 17th, 2008, 11:13am » |
 Quote Quote  Modify Modify
|
on Jun 29th, 2007, 3:11am, towr wrote:| You can reduce it to a largest common 'substring' problem. |
|
what mechanism should be used to convert tree into string(given tree is unlabelled)? how do u label the nodes of binary tree sothat we can apply Longest Common Substring algorithm?
|
| « Last Edit: Mar 17th, 2008, 11:14am by m_aakash » |
 IP Logged IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: largest common subtree
« Reply #11 on: Mar 17th, 2008, 11:35am » |
 Quote Quote  Modify Modify
|
on Mar 17th, 2008, 11:13am, m_aakash wrote:| what mechanism should be used to convert tree into string(given tree is unlabelled)? how do u label the nodes of binary tree sothat we can apply Longest Common Substring algorithm? |
|
I would use parenthesis to denote which nodes are part of the same subtree.
Like ((1)2((3)4(5))) for the tree
2
/ \
1 4
/ \
3 5
If the value of nodes doesn't matter, just don't write anything, and only keep the parenthesis structure. (()(()()))
|
| « Last Edit: Mar 17th, 2008, 11:36am by towr » |
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
m_aakash
Junior Member
 

Posts: 96
|
 |
Re: largest common subtree
« Reply #12 on: Mar 17th, 2008, 12:05pm » |
 Quote Quote  Modify Modify
|
on Mar 17th, 2008, 11:35am, towr wrote:
I would use parenthesis to denote which nodes are part of the same subtree.
Like ((1)2((3)4(5))) for the tree
2
/ \
1 4
/ \
3 5
If the value of nodes doesn't matter, just don't write anything, and only keep the parenthesis structure. (()(()())) |
|
good one. how did i miss this idea?
|
|
 IP Logged IP Logged |
|
|
|
Hippo
Uberpuzzler
    

Gender: 
Posts: 919
|
 |
Re: largest common subtree
« Reply #13 on: Mar 17th, 2008, 1:39pm » |
 Quote Quote  Modify Modify
|
on Mar 17th, 2008, 11:35am, towr wrote:
I am not sure ... probably the longest substring neednot match the biggest subtree.
You must look only for well closed expressions ...
|
|
 IP Logged IP Logged |
|
|
|
m_aakash
Junior Member
 

Posts: 96
|
 |
Re: largest common subtree
« Reply #14 on: Mar 17th, 2008, 10:55pm » |
 Quote Quote  Modify Modify
|
on Mar 17th, 2008, 1:39pm, Hippo wrote:
I am not sure ... probably the longest substring neednot match the biggest subtree.
You must look only for well closed expressions ... |
|
can you give a counter example or prove that it doesnot work?
|
|
 IP Logged IP Logged |
|
|
|
totobogy
Newbie


Posts: 3
|
 |
Re: largest common subtree
« Reply #15 on: Mar 18th, 2008, 4:12am » |
 Quote Quote  Modify Modify
|
One thing that needs to be taken care of in using paranthesis to represent structure is the position of single child - whether it is the left or the right child. A node with a single left child is structurally different from a node with a single right child.
A solution would be to explicitly represent the missing children using a flag, say 'B'.
thus ((),B) can be identified as diff from (B,())
|
|
 IP Logged IP Logged |
|
|
|
Hippo
Uberpuzzler
    

Gender: 
Posts: 919
|
 |
Re: largest common subtree
« Reply #16 on: Mar 18th, 2008, 7:12am » |
 Quote Quote  Modify Modify
|
on Mar 18th, 2008, 4:12am, totobogy wrote:One thing that needs to be taken care of in using paranthesis to represent structure is the position of single child - whether it is the left or the right child. A node with a single left child is structurally different from a node with a single right child.
A solution would be to explicitly represent the missing children using a flag, say 'B'.
thus ((),B) can be identified as diff from (B,())
|
|
You can use parenteses around pointers instead ... so nil pointer will be represented as ().
So ((()()),()) is different from ((),(()())).
on Mar 17th, 2008, 10:55pm, m_aakash wrote:
can you give a counter example or prove that it doesnot work? |
|
Later if noone else gives ... 
|
| « Last Edit: Mar 19th, 2008, 3:12pm by Hippo » |
 IP Logged IP Logged |
|
|
|
johny_cage
Full Member
  

Gender: 
Posts: 155
|
 |
Re: largest common subtree
« Reply #17 on: Mar 19th, 2008, 3:21am » |
 Quote Quote  Modify Modify
|
whats the time complexity of the above mentioned algorthms, i.e the one with string matching patters?
Can't we lower down it
|
|
 IP Logged IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: largest common subtree
« Reply #18 on: Mar 19th, 2008, 3:58am » |
 Quote Quote  Modify Modify
|
on Mar 19th, 2008, 3:21am, johny_cage wrote:| whats the time complexity of the above mentioned algorthms, i.e the one with string matching patters? |
|
If we can use a "longest common substring" algorithm, then we can do at least O(nm).
Quote:Can't we lower down it |
|
We could use an incremental hash, and use that to hash up every subtree in the first tree, then check for every subtree in the other tree whether it has an entry in the hashtable. With a good hash function, it should be O(n+m). In the worst case it'll still be quadratic, though.
|
| « Last Edit: Mar 19th, 2008, 3:58am by towr » |
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
alexeigor
Newbie


Posts: 45
|
 |
Re: largest common subtree
« Reply #19 on: Mar 19th, 2008, 12:32pm » |
 Quote Quote  Modify Modify
|
on Mar 19th, 2008, 3:58am, towr wrote:
If we can use a "longest common substring" algorithm, then we can do at least O(nm).
|
|
We can use suffix tree for longest common substring problem and get O(n+m) time.
|
| « Last Edit: Mar 19th, 2008, 12:33pm by alexeigor » |
 IP Logged IP Logged |
|
|
|
Hippo
Uberpuzzler
    

Gender: 
Posts: 919
|
 |
Re: largest common subtree
« Reply #20 on: Mar 19th, 2008, 3:10pm » |
 Quote Quote  Modify Modify
|
OK, explicitly:
((()((((()())(()()))(()()))()))((()((()())(()())))()))
and
((()(((((()(()()))(()()))((()())()))()))((()((()(()()))(()())))()))
what is the longest common substring?
Is it ()))()))((()((()? And what is the larest common subtree?
Is it (()())?
(Sorry for not trying to create the smallest counter example  ) )
Actually I didn't think much about the algorithm, but my would process "by induction" increasing tree heights and finding equivalence classes of such trees.
Parents of those who are not in the equivalence class shared by both trees neednot be processed so the process can be stopped early. The equivalence class with the most vertices found during the process is the winner.
So start with the DFS and partition (lists) vertices of both trees by their height (length of the longest path to the leaf).
Process the vertices in order of increasing height. Vertices on level 0 are of the same equivalence class 1. Class 0 corresponds to null pointer.
So far algorithm numbered k different equivalence classes and we start processing 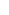 th level. th level.
Hash key created by pair (L,R) where L is the equivalence class number of the left son and R is the equivalence class number of the right son. If the pair is already hashed vertex belongs to already existing class (set info that corresponding tree contains vertex in this equivalence class and if both trees contain a vertex in the class, remember that for current level there is common subtree and check the size of the subtree with the current maximal comon subtree size). If the pair haven't been in the hash increment k the number of equivalence classes, store k as the name of the class, size obtained by sum of subtree sizes plus 1 and set the info that the corresponding tree contains vertex in the class). When all 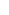 level vertices were processed and no common subtree was found on this level, process can be terminated. Even without this condition the algorithm hashes O(n) vertices in expected O(n) time. Preprocessing took O(n) time as well. level vertices were processed and no common subtree was found on this level, process can be terminated. Even without this condition the algorithm hashes O(n) vertices in expected O(n) time. Preprocessing took O(n) time as well.
Actually as the number of leaves is higher then the number of other vertices there is no reason for "premature termination".
Easier algorithm just performs DFS on the first tree and in postorder updates hash records similarly as in the previous algorithm. Now the equivalence classes will not be numbered by levels but this is no problem.
When traversing 2nd tree each pair which is hashed and was hashed by the first tree is candidate for the maximal common subtree. This will cost O(n) as well and does not require preprocessing.
|
| « Last Edit: Mar 20th, 2008, 1:57pm by Hippo » |
 IP Logged IP Logged |
|
|
|
totobogy
Newbie


Posts: 3
|
 |
Re: largest common subtree
« Reply #21 on: Mar 19th, 2008, 10:35pm » |
 Quote Quote  Modify Modify
|
W.r.t your example above, you need to look for Longest Common 'Well-Formed' Substring and not merely Longest substring. (Well-formed here means properly nested parenthesis).
|
|
 IP Logged IP Logged |
|
|
|
m_aakash
Junior Member
 

Posts: 96
|
 |
Re: largest common subtree
« Reply #22 on: Mar 19th, 2008, 11:17pm » |
 Quote Quote  Modify Modify
|
on Mar 17th, 2008, 11:13am, m_aakash wrote:
what mechanism should be used to convert tree into string(given tree is unlabelled)? how do u label the nodes of binary tree sothat we can apply Longest Common Substring algorithm? |
|
one way to convert tree into string is to assign a label to each edge in particular assign 0 to left edge and 1 to right edge in case of binary tree. for a null edge assign a different value.
|
| « Last Edit: Mar 19th, 2008, 11:24pm by m_aakash » |
 IP Logged IP Logged |
|
|
|
Hippo
Uberpuzzler
    

Gender: 
Posts: 919
|
 |
Re: largest common subtree
« Reply #23 on: Mar 20th, 2008, 12:31am » |
 Quote Quote  Modify Modify
|
on Mar 17th, 2008, 1:39pm, Hippo wrote:
I am not sure ... probably the longest substring neednot match the biggest subtree.
You must look only for well closed expressions ... |
|
on Mar 19th, 2008, 10:35pm, totobogy wrote:| W.r.t your example above, you need to look for Longest Common 'Well-Formed' Substring and not merely Longest substring. (Well-formed here means properly nested parenthesis). |
|
on Mar 20th, 2008, 12:38am, totobogy wrote:| ohh.. sorry didn't see your comment |
|
No problem 
|
| « Last Edit: Mar 21st, 2008, 12:19pm by Hippo » |
 IP Logged IP Logged |
|
|
|
totobogy
Newbie


Posts: 3
|
 |
Re: largest common subtree
« Reply #24 on: Mar 20th, 2008, 12:38am » |
 Quote Quote  Modify Modify
|
ohh.. sorry didn't see your comment
|
|
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register