Author |
Topic: Random Chord Intersection (Read 5023 times) |
|
william wu
wu::riddles Administrator
Gender: 
Posts: 1291
|
 |
Random Chord Intersection
« on: Dec 15th, 2004, 8:51pm » |
 Quote  Modify
|
RANDOM CHORD INTERSECTION
Two chords are drawn at random on a circle. What is the probability that these chords intersect?
Source: Piyush Shanker
Note 1: A "random chord" is generated in the following intuitive way: Draw two points uniformly at random over the circumference of the circle. Then connect those two points.
Note 2: There is a clever way to solve this very quickly, without evaluating any integrals.
======================
Harder variants (added 7:05 PM 12/18/2004)
- Compute the probability distribution of the number of chord intersections when three chords are dropped.
- What about N chords?
|
| « Last Edit: Dec 18th, 2004, 7:08pm by william wu » |
 IP Logged |
[ wu ] : http://wuriddles.com / http://forums.wuriddles.com
|
|
|
Noke Lieu
Uberpuzzler
pen... paper... let's go! (and bit of plastic)
Gender:
Posts: 1884
|
|
Re: Random Chord Intersection
« Reply #1 on: Dec 15th, 2004, 10:40pm » |
Quote Modify
|
Going to have a stab... probability isn't my strong point. Probably. Accordingly, I reckon that if I set off in the right direction, not going to be able to wrap it up.
Assuming- not sure what difference it makes- that the chords are distinct. Oh that goes for points too.
Two points on the circle. Cut into two arcs... 2[pi]r(a) and 2[pi](a-1).
For the chords to NOT intersect... need the next two points on the same arc.
That makes me think of this
Poop. Run out of steam- and time. ...
|
|
IP Logged |
a shade of wit and the art of farce.
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 7527
|
|
Re: Random Chord Intersection
« Reply #2 on: Dec 16th, 2004, 12:20am » |
Quote Modify
|
Basically, you take 4 points on the circle and you pair them. With 4 points, there are 3 ways to pair them, only one of them with an intersection. So the probability is 1/3.
|
|
IP Logged |
|
|
|
Noke Lieu
Uberpuzzler
pen... paper... let's go! (and bit of plastic)
Gender:
Posts: 1884
|
|
Re: Random Chord Intersection
« Reply #3 on: Dec 16th, 2004, 3:40pm » |
Quote Modify
|
DAMN IT!
That's how I started... I figured it wasn't enough. Oh well.
|
|
IP Logged |
a shade of wit and the art of farce.
|
|
|
Sir Col
Uberpuzzler
impudens simia et macrologus profundus fabulae
Gender:
Posts: 1825
|
|
Re: Random Chord Intersection
« Reply #4 on: Dec 16th, 2004, 4:48pm » |
Quote Modify
|
As I couldn't think of an approach as clever as Grimbal's, I ignored note 2 and solved it (inelegantly) by integration...
Between any two points on a circle there are two arcs; call them s1 and s2. Let P(point in s1)=p and P(point in s2)=q=1-p.
For a given p, P(two chords intersect)=2p(1-p)=2p-2p2.
As we are dealing with a uniform distribution, we integrate 2p-2p2 between 0 and 1 to give, P(intersection)=1/3.
I suppose a challenging extension would be to explore the probability of three random chords intersecting; that is, none, two, or three. Even harder, if X represents the number of points of intersection, find P(X=r), where r=0,1,2,3.
|
|
IP Logged |
mathschallenge.net / projecteuler.net
|
|
|
william wu
wu::riddles Administrator
Gender:
Posts: 1291
|
|
Re: Random Chord Intersection
« Reply #5 on: Dec 18th, 2004, 6:56pm » |
Quote Modify
|
In case anyone is unclear about the slick solution, the following picture I made should clear it up. In the diagram below, we have a circle with four points A, B, C, and D randomly placed along the circumference:
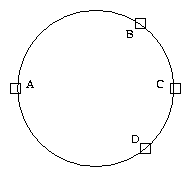
These points represent the endpoints of the two chords, and due to the facts that 1) the points are distributed uniformly at random, and 2) we have circular symmetry, the actual positions do not matter. All that matters is which endpoints belong to which chords.
Without loss of generality, let's assume point A is an endpoint for the first chord. Then we will have an intersection only if the other endpoint of this first chord is point C. So the probability of intersection is 1/3.
====
Using the same geometrical inspirations as above, but with six points on the circumference, I tried Sir Col's challenge. This problem was quite a bit harder since there were many more cases. I broke it up into the following scenarios:
::
0) 0 intersections
1a) 1 intersection, given that the first chord is not intersected
1b) 1 intersection, given that the first chord is intersected
2) 2 intersections
3) 3 intersections
::
Also, I used the 1/3 result from the original problem many times. In the end, I computed the following answers (hidden; highlight the area below with your mouse to reveal):
::
Pr(X = 0) = 1/3
Pr(X = 1) = 2/5
Pr(X = 2) = 1/5
Pr(X = 3) = 1/15
::
The distribution sums to 1 (a good check), and it agrees with a MATLAB simulation I wrote, so it's right  You can adjust "numChords" in the code below to simulate the problem for higher numbers of chords -- but don't go too high or you'll be sorry. The simulation unwraps the circle into a unit interval, draws pairs of points uniformly at random, and then uses the observation that two chords intersect iff exactly one of the endpoints of a chord lies in the interval spanned by the endpoints of the other chord.
Code:
%RANDOMCHORDINTERSECTION Uses simulation to determine the distribution of
%number of intersections when chords are dropped uniformly at random onto a
%circle. - William Wu 6:41 PM 12/18/2004
clear; clc; close all;
numChords = 3;
numTrials = 100000;
numIntersections = zeros(1,numTrials);
maxIntersections = nchoosek(numChords,2);
for k=1:numTrials
chords = rand(numChords,2);
chords = sort(chords')'; % second column has higher values
idx = nchoosek(1:numChords,2);
for m=1:maxIntersections
numIntersections(k) = numIntersections(k) + ...
overlapCheck( chords(idx(m,1),:),chords(idx(m,2),:) );
end
end
[N,X] = hist(numIntersections,0:maxIntersections);
bar(X,N/numTrials); grid on;
title(sprintf('empirical distribution with %d chords and %d trials',numChords,numTrials));
fprintf(1,'empirical distribution: %s\n',num2str(N/numTrials));
function overlapFlag = overlapCheck(a,b)
% a(1) is within the bounds of b, and a(2) is outside bounds
x = (b(1)<a(1))&(a(1)< b(2))&(b(2) < a(2));
% or, a(2) is within the bounds of b, and a(1) is outside bounds
y = (b(1)<a(2))&(a(2)< b(2))&(b(1) > a(1));
overlapFlag = (x | y);
|
|
|
| « Last Edit: Dec 18th, 2004, 7:30pm by william wu » |
IP Logged |
[ wu ] : http://wuriddles.com / http://forums.wuriddles.com
|
|
|
Sir Col
Uberpuzzler
impudens simia et macrologus profundus fabulae
Gender:
Posts: 1825
|
|
Re: Random Chord Intersection
« Reply #6 on: Dec 19th, 2004, 3:52am » |
Quote Modify
|
I've spent quite a bit of time on this and I don't think that there is a general solution for the number of intersections. I have, however, derived a formula for the probability of no intersections with r chords...
For r chords there will be n=2r points on the circle.
Given the first chord is connected to one of these points there are (n-1) other end points it can connect to.
The end point of the "second" chord can connect to (n-3) other points.
Similarly the other chords will be able to connect to (n-5), (n-7), ..., 5, 3, 1 other end points.
Therefore, the number of ways of drawing r chords, R, is given by,
R = (n-1)(n-3)...5*3*1 = (2r-1)(2r-3)..*3*1 = (2r)!/(r!*2r)
The hard part is finding the number of ways that no chords can intersect. After a little investigating I found an amazing connection with Catalan numbers.
Imagine that the n points are numbers sequentially 1 to n around the circumference of the circle.
If one of the chords is (1,3), then the chord connected to 2 must intersect (1,3). So there must be an even number of points between each pair of connected points, but even this does not guarantee.
I then was reminded of a similar investigation. I'm not sure what it is called, so I shall call it the "bracket string" problem: given r pairs of brackets (one left and one right), how many bracket strings can we form?
For example,
r=1: () [)( is not considered a bracket string]
r=2: ()(), (())
r=3: ()()(), ()(()), (())(), (()()), ((()))
The number of solutions are given by the rth Catalan number: C=(2r)!/((r+1)!r!). More importantly, it can be seen that if the left and right brackets represent end points of a chord, the number of solutions to this problem is equivalent to the number of solutions to the number of non-intersecting chords.
Hence P(Xr=0) = C/R = [(2r)!/((r+1)!r!)]/[(2r)!/(r!*2r)] = 2r/(r+1)!, where Xr is the number of intersections for r chords.
For example, P(X1=0)=1, P(X2=0)=2/3, P(X3=0)=1/3, P(X4=0)=2/15.
Obviously the complement of this gives the probability that there is at least one intersection, but given the complexity of the derivation for this particular case, I doubt we're going to find a general solution for each of the separate probabilities.
|
|
IP Logged |
mathschallenge.net / projecteuler.net
|
|
|
william wu
wu::riddles Administrator
Gender:
Posts: 1291
|
|
Re: Random Chord Intersection
« Reply #7 on: Dec 19th, 2004, 4:10pm » |
Quote Modify
|
That's a nice observation Sir Col. I don't feel certain though about whether a general solution is not possible for n chords ... I was hoping for a recursive expression.
It's interesting to note that the parenthetical analogy seems to break down when counting a nonzero number of intersections. For instance, consider the string
(()())
which can be interpreted as the following for 0 intersections:
( () () )
or the following for one intersection:
( ()() )
or the following for two intersections:
( ()() )
Here is some more empirical data for higher chord values; the true answers would round to some nice rationals:
===
4 chords:
0.13374
0.26962
0.26681
0.18711
0.09545
0.03731
0.00996
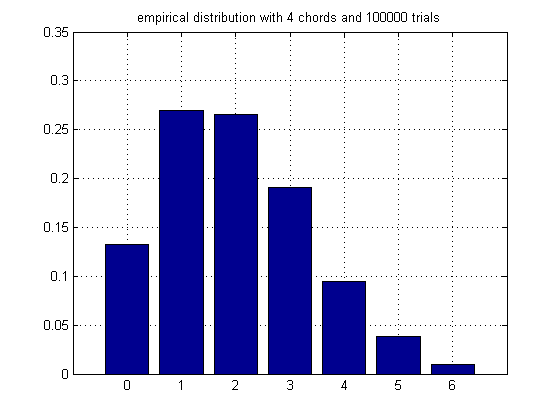
empirical average: 1.9980
theoretical mean: 2
===
5 chords:
0.04484
0.12675
0.1907
0.20846
0.17365
0.12194
0.07316
0.03806
0.01566
0.00553
0.00125
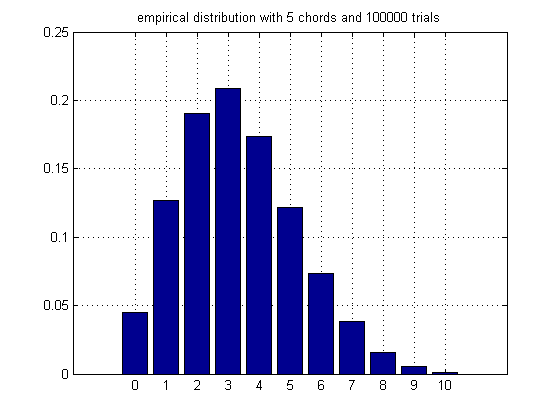
empirical average = 3.3308
theoretical mean = 10/3
===
6 chords:
0.01235
0.04757
0.09709
0.13683
0.1578
0.15587
0.13212
0.10195
0.06926
0.04402
0.02527
0.01175
0.00548
0.00191
0.00066
7e-005
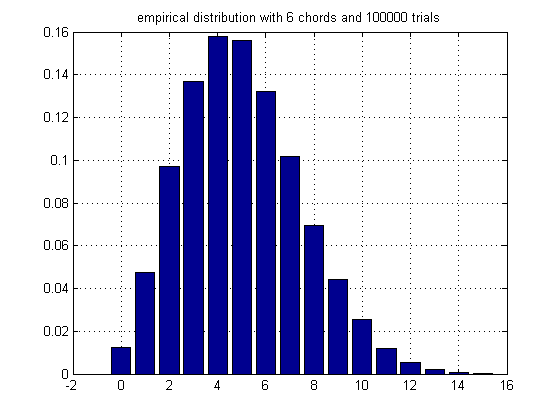
empirical mean: 5.0023
empirical variance: 6.0224
theoretical mean: 5
Note the nice shapes. I believe the asymptotic distribution is Gaussian. For N chords, we can express the number of intersections as the sum of C(N,2) indicator random variables, each taking on the value of 1 if a particular pair of chords intersects (which occurs with probability 1/3). These indicator variables are not independent. However, in the limit when we have many chords, they are almost independent. From CLT we know that the sum of K iid random variables is Gaussian with mean K[mu] and variance K[sigma]2. There are also some more precise variants of the CLT specifically for weakly dependent random variables.
|
| « Last Edit: Dec 19th, 2004, 4:47pm by william wu » |
IP Logged |
[ wu ] : http://wuriddles.com / http://forums.wuriddles.com
|
|
|
Sir Col
Uberpuzzler
impudens simia et macrologus profundus fabulae
Gender:
Posts: 1825
|
Using your experimental results and the formula I derived for the number of ways we can connect r chords: R = (2r)!/(r!*2r), we can obtain an estimate of frequencies/theoretical probabilities.
I've included a spreadsheet with a summary of the calculations. For example, when r=4, we obtain:
P(X=0)=14/105
P(X=1)=28/105
P(X=2)=28/105
P(X=3)=20/105
P(X=4)=10/105
P(X=5)=4/105
P(X=6)=1/105
The numerators for P(X=0) are the Catalan numbers: 1, 2, 5, 14, 42, 132, ..., but maybe someone else can recognise the other numerators? Beware though, as you can see that the expected frequencies become less reliable as r increases. It estimated P(X=0)=128/10395 for r=6, when it should be 132/10395.
|
|
IP Logged |
mathschallenge.net / projecteuler.net
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print
random_chords.xls