 Author
Author |
Topic: Connect the 6 dots together, is this impossible? (Read 21432 times) |
|
Etard94
Newbie


Posts: 1
|
 |
Connect the 6 dots together, is this impossible?
« on: Nov 1st, 2008, 11:38pm » |
 Quote Quote  Modify Modify
|
So there is this puzzle, a puzzle which everybody on every site which has this puzzle has claimed to be impossible, but according to my maths teacher is not.
Please, I'm like dying for the solution, like literally! And if you can't find the solution, recommend a forum which i can post this puzzle on and get some good responses.
And apparently it's a maths problem, so maybe you could maths to solve it, i have no idea ;S
. . .
. . .
Okay, well you have to make each dot connect to the other 5 dots. So like, if you start with the top left dot and connect it to the other 5, do the same to every other dot. So you'll end up with a lot of lines, and they can also curve around the dots, they don't have to go straight.
But the thing is, you can't cross the lines, so they can't touch.
IS THIS REALLY IMPOSSIBLE!? 
|
|
 IP Logged IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: Connect the 6 dots together, is this impossibl
« Reply #1 on: Nov 1st, 2008, 11:46pm » |
 Quote Quote  Modify Modify
|
It's [edit: not] known as the utilities problem, and it is in fact impossible. There is a nice proof here.
|
| « Last Edit: Nov 2nd, 2008, 11:47am by Eigenray » |
 IP Logged IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: Connect the 6 dots together, is this impossibl  ut.png ut.png
« Reply #2 on: Nov 2nd, 2008, 7:48am » |
 Quote Quote  Modify Modify
|
You can do the utility problem on a torus (donut).
But in the plane (or equivalently on the surface of a sphere) it is impossible (as explained in Eigenray's link).
If each dot has to be connected to all five other dots, then it's not quite the same problem, but even more difficult. However, it can still be solved on the surface of some object* (as long as it has enough holes in the right places), just not on the plane.
[edit]* Actually, it seems this one can also still be done on a torus.[/edit]
[edit2]See attachment, line-ends with the same color are connected over the torus/donut (i.e. top and bottom, and left and right wrap together) [/edit2]
|
| « Last Edit: Nov 2nd, 2008, 8:23am by towr » |
 IP Logged IP Logged |

Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: Connect the 6 dots together, is this impossibl
« Reply #3 on: Nov 2nd, 2008, 11:46am » |
 Quote Quote  Modify Modify
|
Whoops, you're right. I saw 2 rows of 3 dots and my mind jumped straight to K3,3.
Even if there were only 5 dots, it would still be impossible (in the plane). The interesting thing is that the converse holds as well: a graph can be embedded in the plane if and only if it doesn't contain either the utilities graph (K3,3) or the complete graph on 5 vertices (K5) as a minor (that is, by removing vertices, edges, or contracting edges).
Edit: There are five dots! How many do you see now?
|
| « Last Edit: Nov 2nd, 2008, 1:46pm by Eigenray » |
 IP Logged IP Logged |
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 2084
|
 |
Re: Connect the 6 dots together, is this impossibl
« Reply #4 on: Nov 2nd, 2008, 1:03pm » |
 Quote Quote  Modify Modify
|
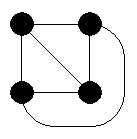
on Nov 2nd, 2008, 11:46am, Eigenray wrote:| Even if there were only 4 dots, it would still be impossible (in the plane). |
|
Eh?
--SMQ
|
|
 IP Logged IP Logged |
--SMQ
|
|
|
Hippo
Uberpuzzler
    

Gender: 
Posts: 919
|
 |
Re: Connect the 6 dots together, is this impossibl
« Reply #5 on: Nov 2nd, 2008, 1:15pm » |
 Quote Quote  Modify Modify
|
on Nov 2nd, 2008, 11:46am, Eigenray wrote:Whoops, you're right. I saw 2 rows of 3 dots and my mind jumped straight to K3,3.
Even if there were only 4 dots, it would still be impossible (in the plane). The interesting thing is that the converse holds as well: a graph can be embedded in the plane if and only if it doesn't contain either the utilities graph (K3,3) or the complete graph on 4 vertices (K4) as a minor (that is, by removing vertices, edges, or contracting edges). |
|
Wow, weeker side of our algebraic hero?
Kuratowski theorem talks about divisions of K3,3 or K5.
And tetrahedron can be projected on sphere easily  . .
Sorry for magnifying that, but until now, I felt everyone expect you Eigenray can be cought as beeing mistaken occasionaly so please take it more like a compliment 
|
| « Last Edit: Nov 2nd, 2008, 1:28pm by Hippo » |
 IP Logged IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: Connect the 6 dots together, is this impossibl
« Reply #6 on: Nov 2nd, 2008, 1:43pm » |
 Quote Quote  Modify Modify
|
on Nov 2nd, 2008, 1:03pm, SMQ wrote:
Strange... I see five. Are you quite sure? 
Well, looks like I've embarrassed myself enough for one thread. Cheerio!
|
| « Last Edit: Nov 2nd, 2008, 1:52pm by Eigenray » |
 IP Logged IP Logged |
|
|
|
rmsgrey
Uberpuzzler
    

    
Gender: 
Posts: 2873
|
 |
Re: Connect the 6 dots together, is this impossibl
« Reply #7 on: Nov 2nd, 2008, 2:00pm » |
 Quote Quote  Modify Modify
|
If memory serves, K7 can also be done on a torus, though not K8
|
|
 IP Logged IP Logged |
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 7527
|
 |
Re: Connect the 6 dots together, is this impossibl  connect7.gif connect7.gif
« Reply #8 on: Dec 6th, 2008, 12:57pm » |
 Quote Quote  Modify Modify
|
It does.
|
|
 IP Logged IP Logged |

|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: Connect the 6 dots together, is this impossibl
« Reply #9 on: Dec 6th, 2008, 1:29pm » |
 Quote Quote  Modify Modify
|
on Dec 6th, 2008, 12:57pm, Grimbal wrote:So obvious once you see it. Wish I thought of it..
|
| « Last Edit: Dec 6th, 2008, 1:30pm by towr » |
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register