Author |
Topic: A parabola and a triangle (Read 5705 times) |
|
pex
Uberpuzzler
Gender: 
Posts: 880
|
 |
A parabola and a triangle
« on: Oct 26th, 2012, 5:26am » |
 Quote  Modify
|
Given are a parabola, and a line intersecting this parabola in two distinct points. Let S be the region bounded by the parabola and the line, and let T be the largest triangle that can be inscribed in S.
Show that the ratio (area of T) : (area of S) is independent of the choice of parabola and line.
(Yes, this is a classic, and probably googlable. I found it interesting regardless.)
|
|
 IP Logged |
|
|
|
Noke Lieu
Uberpuzzler
pen... paper... let's go! (and bit of plastic)
Gender:
Posts: 1884
|
|
Re: A parabola and a triangle
« Reply #1 on: Oct 29th, 2012, 11:20pm » |
Quote Modify
|
ax2+bx+c
area under that = (ax3/3) + (bx2/2)+cx
Area bounded by line and x-axis (mx2/2) + nx
Difference between these two areas = area bounded by parabola and line
(-ax3/3) + ((m-b)x2/2)+(n-c)x
Line and parabola intersect at
ax2+bx+c = mx+n
0=(m-b)x+(n-c)-ax2
the roots of which are (-(m-b)+_sqrt((m-b)2-4a(n-c)) )/2a
Sooo...
Find the difference between root1 and root2 for the horizontal component of the base; plug them back into y=mx+c, and find the differences to work out hte vertical component, then use Pythagoras' theorem to work out the base length...
Find the mean of the two roots to determine the hieght of the triangle... and notice how there has to be a a more elegant (or, indeed, accurate) way... 
It's easier with the constraint that the line's horizontal to the 'vertical' parabola...
|
|
IP Logged |
a shade of wit and the art of farce.
|
|
|
pex
Uberpuzzler
Gender:
Posts: 880
|
|
Re: A parabola and a triangle
« Reply #2 on: Oct 30th, 2012, 1:19am » |
Quote Modify
|
on Oct 29th, 2012, 11:20pm, Noke Lieu wrote:| ... and notice how there has to be a a more elegant (or, indeed, accurate) way... |
|
... yes. Yes, there is  Of all possible parameterizations, you seem to have chosen the least convenient one...
|
|
IP Logged |
|
|
|
Noke Lieu
Uberpuzzler
pen... paper... let's go! (and bit of plastic)
Gender:
Posts: 1884
|
|
Re: A parabola and a triangle
« Reply #3 on: Oct 30th, 2012, 4:11am » |
Quote Modify
|
played for and got!
Needed to reflect my current project...
|
|
IP Logged |
a shade of wit and the art of farce.
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 7527
|
|
Re: A parabola and a triangle
« Reply #4 on: Nov 1st, 2012, 9:18am » |
Quote Modify
|
on Oct 29th, 2012, 11:20pm, Noke Lieu wrote:| It's easier with the constraint that the line's horizontal to the 'vertical' parabola... |
|
Note that you can satisfy that with a linear transform. And such a transform preserves the ratio of surfaces.
|
|
IP Logged |
|
|
|
Immanuel_Bonfils
Junior Member
Posts: 114
|
|
Re: A parabola and a triangle
« Reply #5 on: Nov 15th, 2012, 3:37pm » |
Quote Modify
|
The ratio, already known by Archimedes, is 3/4 .
|
|
IP Logged |
|
|
|
pex
Uberpuzzler
Gender:
Posts: 880
|
on Nov 15th, 2012, 3:37pm, Immanuel_Bonfils wrote:| The ratio, already known by Archimedes, is 3/4 . |
|
Well, I did say it was a classic...  My solution follows below.
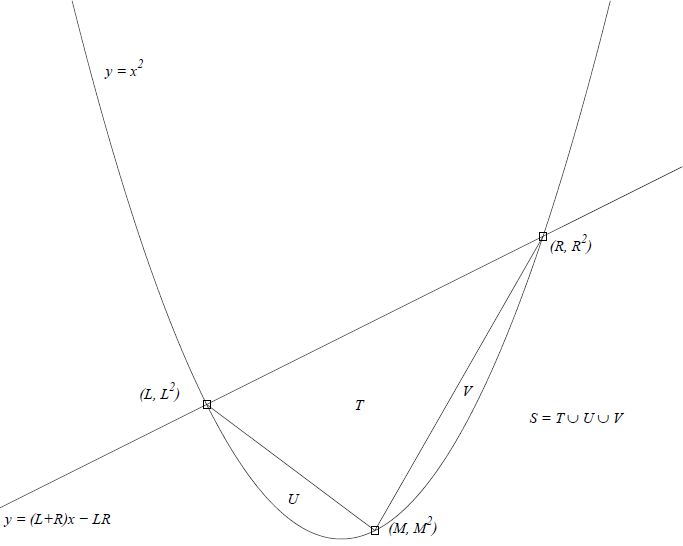
The first thing to realize is that "all parabolas are equal"; that is, we may choose a coordinate system in which the given parabola is described by y = x2.
The second thing to realize is that this problem becomes much easier if we don't parameterize the line as y = Ax + B, but instead in terms of its intersection points with the parabola. Let's say they are (L, L2) and (R, R2), with L < R. It follows that the line has the equation y = (L+R)x - LR.
The area of S is simply integral(x = L..R) [(L+R)x - LR - x2] dx
= [(L+R)x2/2 - LRx - x3/3](x = L..R)
= (L+R)(R2-L2)/2 - LR(R-L) - (R3-L3)/3
= (R-L)/6 ( 3(L+R)2 - 6LR - 2(R2+LR+L2) )
= (R-L)/6 (L2 - 2LR + R2)
= (R-L)3/6.
Now, let us introduce T, the largest triangle that can be inscribed in S. It is obvious that its vertices will be (L, L2), (R, R2), and (M, M2), for some number M with L < M < R.
Refer to the attached figure. We can find the areas of U and V in the same way as we found that of S:
area of U = (M-L)3/6
area of V = (R-M)3/6
and hence, area of T = (area of S) - (area of U) - (area of V)
= (1/6) ((R-L)3 - (M-L)3 - (R-M)3)
= (3/6) (-LR2+L2R +LM2-L2M +MR2-M2R)
= (1/2) (R-L) (-LR-M2+LM+MR)
= (R-L)(M-L)(R-M)/2.
The maximum of this expression is attained at M = (L+R)/2, so that
area of T = (R-L)3/8
and indeed, (area of T) / (area of S) = 3/4.
|
| « Last Edit: Nov 16th, 2012, 4:07pm by pex » |
IP Logged |
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print