 Author
Author |
Topic: Inversion Tutorial. Part 2. (Read 9464 times) |
|
rloginunix
Uberpuzzler
    

Posts: 1029
|
 |
Inversion Tutorial. Part 2.
« on: Sep 13th, 2014, 8:38am » |
 Quote Quote  Modify Modify
|
Inversion with Respect to a Circle in a Real Plane. Part 2. Application.
In "Inversion Tutorial. Part 1." we have looked at a number of basic properties of inversion with respect to a circle. In this part of the tutorial we will apply the gained knowledge to problem solving.
Aside from using inversion to construct a reciprocal of a given linear measure I have identified one inversion with respect to a circle-based problem solving algorithm:
1). Choose a convenient center of inversion.
2). Choose a convenient radius of inversion.
3). Invert the original object(s) with respect to the circle of inversion found in 1) and 2).
4). Solve a (presumably easier) problem in terms of the inverse object(s).
5). Using the preservation of angles, tangent points and other basic properties of inversion convert the solution in terms of the inverse object(s) obtained in 4) into the solution in terms of the original object(s).
|
|
 IP Logged IP Logged |
|
|
|
rloginunix
Uberpuzzler
    

Posts: 1029
|
 |
Re: Inversion Tutorial. Part 2.
« Reply #1 on: Sep 13th, 2014, 8:50am » |
 Quote Quote  Modify Modify
|
Tangent Circles.
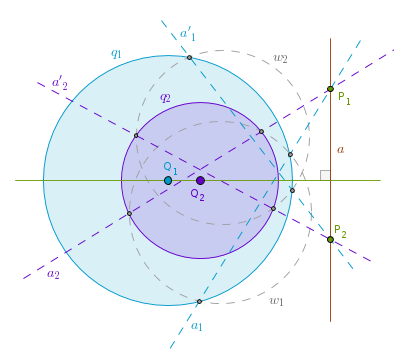
Problem 1. Construct all circles which are tangent to a given circle q(Q, R), pass through a given point P and have their centers located on a straight line passing through P and Q.
Center of inversion.
We know that the circles sought after must pass through P. We also remember that circles passing through the center of inversion become straight lines (which are "easier" to construct). It makes sense then to pick the given point P as a center of inversion - if we somehow construct these straight lines and invert them back then we will have our circles.
Radius of inversion.
It doesn't really matter what we pick but in order to minimize the number of points we need to invert let us choose PA as a radius of inversion:
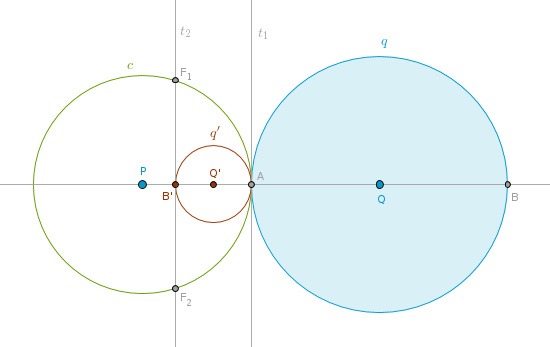
Inversion.
According to ICP17 under the inversion with respect to c(P, PA) q(Q, R) becomes q'(Q', R') - a circle touching c(P, PA) at A internally.
Solution in terms of the inverse objects.
We know how to construct two tangents to the circle q' at A and B' - t1 (at A) and t2 (at B').
Solution in terms of the original objects.
Just because of the way we've picked our circle of inversion the straight line t1 is tangent to c at A. From ICP9 it follows that t1 will invert into a circle passing through P and touching c at A internally. From ICP26 we know that under inversion tangency points are preserved. If t1 and q' touch then their images will also touch. This is exactly what we want and thus the first required circle is constructed - invert t1 with respect to c.
The straight line t2 does not pass through P and intersects c in exactly two points, F1 and F2. From ICP8 it follows that t2 will invert into a circle passing through P, F1, F2. To locate the center of this circle we bisect LineSegment(P, F1). From ICP26 we know that under inversion tangency points are preserved. If t2 and q' touch then their images will also touch. This is exactly what we want and thus the second required circle is constructed - invert t2 with respect to c:
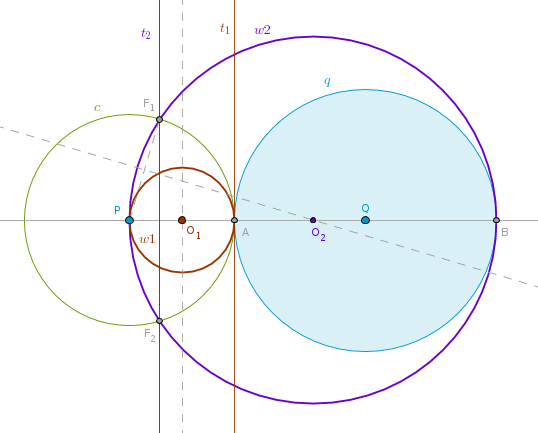
1). Line(P, Q) until it intersects q(Q, R) at A and B.
2). Invert q with respect to c(P, PA) to obtain the circle q'.
3). Tangent t1 to q' at A.
4). Tangent t2 to q' at B'.
5). Invert t1 with respect to c to obtain the circle w1.
6). Invert t2 with respect to c to obtain the circle w2.
You can examine the case when P is inside q yourself.
Now that we went through one problem thoroughly I will move a bit faster.
[edit]
As per rmsgrey's observation (see below) added "and have their centers located on a straight line passing through P and Q" to the end of the problem statement.
[/edit]
|
| « Last Edit: Sep 14th, 2014, 10:36am by rloginunix » |
 IP Logged IP Logged |
|
|
|
rloginunix
Uberpuzzler
    

Posts: 1029
|
 |
Re: Inversion Tutorial. Part 2.
« Reply #2 on: Sep 13th, 2014, 8:58am » |
 Quote Quote  Modify Modify
|
Problem 2. Construct all circles which are tangent to two given circles q1(Q1, R1) and q2(Q2, R2) and pass through a given point P located outside q1 and q2.
Choose P as a center of inversion and make c(P, r) a circle of inversion. Assume that one required circle, w1, is somehow constructed. Under the inversion with respect to c circles q1 and q2 become circles q'1 and q'2 while the circle w1 becomes a straight line t1.
Since tangency points under inversion are preserved it stands to reason that t1 will be a tangent common to both circles, q'1 and q'2. How many common tangents do two circles have? There are several scenarios. Let us consider the most generic one - four common tangents. Inverting these tangents with respect to c locates our circles.
To eliminate the clutter in the drawing below I have constructed just one common tangent t1 and one target circle w1:
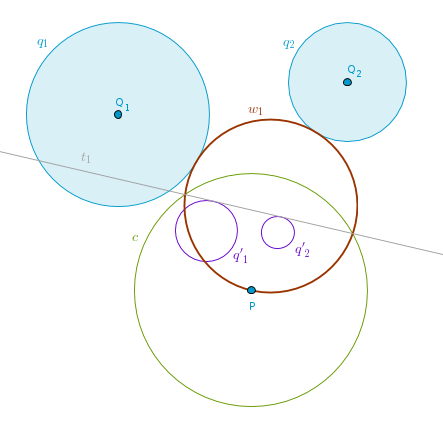
1). Invert the given circles q1 and q2 with respect to c(P, r) to obtain the circles q'1 and q'2.
2). Construct four tangents common to circles q'1 and q'2 - t1, t2, t3, t4.
3). Invert t1, t2, t3, t4 with respect to c(P, r) to obtain the four circles sought after.
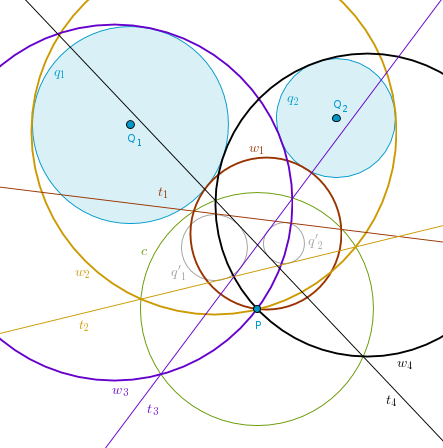
In the most generic case of four circles one will touch both given circles externally (w1), one will touch both circles internally (w2), and each of the two remaining circles will touch one given circle internally and the other externally (w3) and vice versa (w4). In the drawing below I have used color and text to pair up a tangent straight line with its circle that touches both given ones: {t1, w1}, {t2, w2}, {t3, w3} and {t4, w4}:
|
|
 IP Logged IP Logged |
|
|
|
rloginunix
Uberpuzzler
    

Posts: 1029
|
 |
Re: Inversion Tutorial. Part 2.
« Reply #3 on: Sep 13th, 2014, 9:07am » |
 Quote Quote  Modify Modify
|
Problem 3. Given three circles q1, q2 and q3, which intersect at a point P, construct all circles which are tangent to q1, q2 and q3.
Choose P as a center of inversion. Make the radius of inversion r such that c(P, r) intersects all three circles. Under the inversion with respect to c(P, r) the given circles q1, q2 and q3, which pass through P, will invert into the straight lines q'1, q'2 and q'3. And since the original circles do not touch but intersect pairwise - so will the straight lines. By doing so they will delineate a triangle, LMN in the drawing below.
We now can construct four circles each of which is tangent to all three straight lines - one incircle and three excircles. Inverted back with respect to c these circles will preserve their points of tangency and will become the circles sought after. In the drawing below I have constructed an incircle, w'1, and its inverse - a circle w1 that touches all three given circles internally:
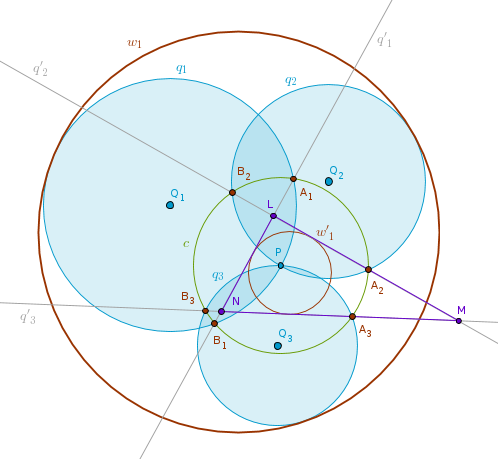
1). Invert the given circles q1, q2 and q3 with respect to c(P, r) to obtain the straight lines q'1, q'2 and q'3 which will delineate a triangle.
2). Construct four circles each of which is tangent to q'1, q'2 and q'3 - w'1, w'2, w'3, w'4 (one incircle and three excircles).
3). Invert w'1, w'2, w'3, w'4 with respect to c(P, r) to obtain the four circles sought after.
In the drawing below I have used text to pair up a circle tangent to q'1, q'2 and q'3 (a dashed line of one color) with its circle that touches all three given circles (a solid line of a different color): {w'1, w1}, {w'2, w2}, {w'3, w3} and {w'4, w4}:
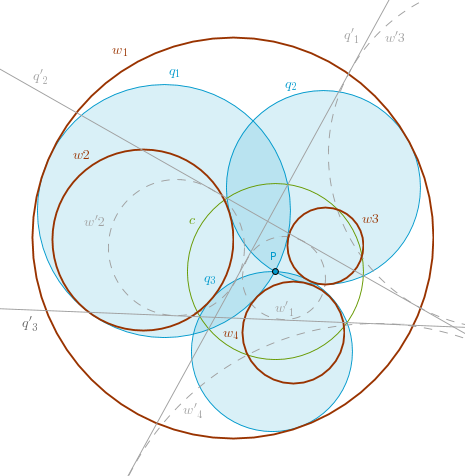
|
|
 IP Logged IP Logged |
|
|
|
rloginunix
Uberpuzzler
    

Posts: 1029
|
 |
Re: Inversion Tutorial. Part 2.
« Reply #4 on: Sep 13th, 2014, 9:53am » |
 Quote Quote  Modify Modify
|
Problem 4. The Three-Circle Problem of Apollonius: construct all circles which are tangent to three given circles q1(Q1, R1), q2(Q2, R2) and q3(Q3, R3).
To avoid the ambiguity and to refresh our memory let us recall the following two definitions. Two circles q1(Q1, R1) and q2(Q2, R2) touch externally if the distance between their centers is equal to the sum of their radii: LineSegment(Q1, Q2) = R1 + R2. Two circles q1(Q1, R1) and q2(Q2, R2) touch internally if the distance between their centers is equal to the difference between their radii: LineSegment(Q1, Q2) = |R1 - R2|.
(Please note that below I will use the symbol R often and with different circles. It does not mean that the length of R is always the same - it is different for each different circle. I simply want to avoid the need for extra indexing and want to stress that the idea behind an operation is every time the same.)
The three-circle problem of Apollonius in general has eight solutions which can be grouped into three sets of circles. There are two circles in the first set - one touches all three given circles internally and the other touches all three given circles externally.
The remaining two sets of solutions have three circles each. The circles in one solution set touch in turn each one of the given circles externally while touching the remaining two given circles internally. The circles in the other solution set touch in turn each one of the given circles internally while touching the remaining two given circles externally.
To obtain these solutions we will employ two main ideas. The first idea is to reduce this problem to an already solved one - Problem 2. The second idea is similar to the one used in constructing tangents common to two circles:
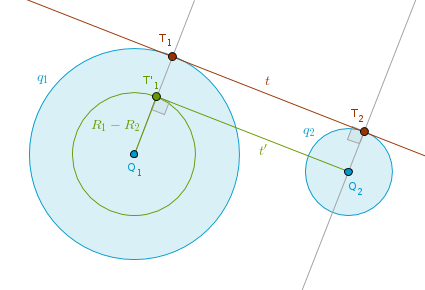
Without the loss of generality let us assume that R1 >= R2 so that when we say "R1 - R2" while constructing an external common tangent it makes geometric sense:
1). Circle(Q1, R1 - R2).
2). Tangent t' to Circle(Q1, R1 - R2) through Q2 to locate T'1.
3). Ray(Q1, T'1) until it intersects q1 at T1.
4). Line through Q2 parallel to Ray(Q1, T'1) until it intersects q2 at T2.
5). Line(T1, T2) is the common tangent sought after.
Let us call the above an "R1 - R2" idea. To construct a common internal tangent you would construct Circle(Q2, R1 + R2): an "R1 + R2" idea.
Back to the problem of Apollonius. Let us first construct the two circles that touch all three given circles internally and externally.
To construct the circle that touches all three given circles internally we will use the external tangent common to two circles "R1 - R2" idea.
Without the loss of generality let us assume that we have sorted the given radii in such a way that, say, R3 is the smallest: R1 >= R3 and R2 >= R3. Construct two intermediate helper circles - k1(Q1, R1 - R3) and k2(Q2, R2 - R3).
Rephrase the Problem 2 as "construct all circles which are tangent to two given circles k1 and k2 and pass through Q3".
To solve this problem we invert the circles k1 and k2 into the circles k'1 and k'2, construct two common external tangents to k'1 and k'2 - t1 and t2 - and invert them.
In the drawing below I have constructed and inverted t1 to obtain the circle w'1(W1, R) which passes through Q3 and touches k1 and k2 internally:
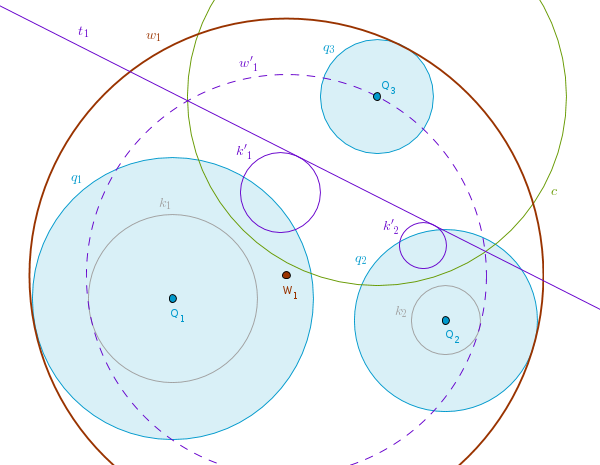
We see that w'1 is almost exactly what we want - it is concentric with the target circle and its radius is by R3 smaller. We keep the center W1, increase R by R3 and we have the first solution circle w1 that touches all three given circles internally.
In the next drawing I have constructed and inverted t2 to obtain the circle w'2(W2, R) which passes through Q3 and touches k1 and k2 externally. We keep W2 as a center, decrease R by R3 and we have the second solution circle w2 that touches all three given circles externally:
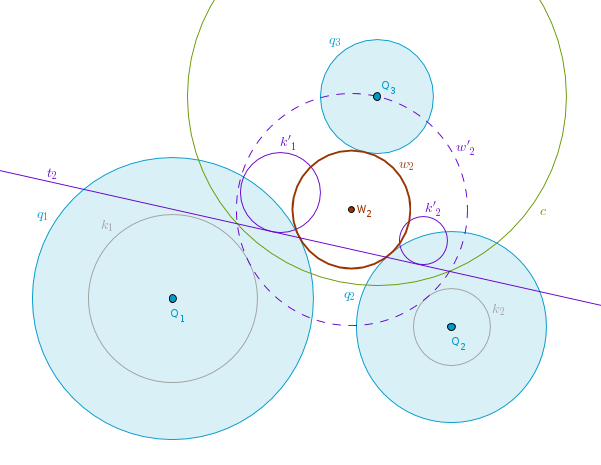
To construct the remaining six circles we will use the internal tangent common to two circles "R1 + R2" idea. All these circles are constructed in the same way so I will cover just one set of two solution circles and you should be able to finish the rest yourself.
To make the sizes of the solution circles manageable I made the given circles a bit smaller this time.
Let us work with, say, q1. We shall construct one circle that touches q1 externally while touching q2 and q3 internally and one circle that touches q1 internally while touching q2 and q3 externally.
Construct the circles k2(Q2, R2 + R1) and k3(Q3, R3 + R1). Invert them with respect to c(Q1, r) to obtain the circles k'2 and k'3. Construct two external tangents common to k'2 and k'3 - t3 and t4. Invert t3 with respect to c(Q1, r) to obtain the circle w'3(W3, R) which passes through Q1 and touches k2 and k3 internally. Keep W3 as a center, decrease R by R1 to obtain the circle w3 that touches q1 externally while touching q2 and q3 internally:
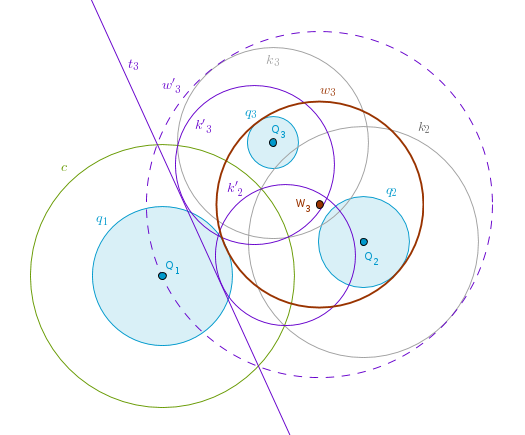
Invert t4 with respect to c(Q1, r) to obtain the circle w'4(W4, R) which passes through Q1 and touches k2 and k3 externally. Keep W4 as a center, increase R by R1 to obtain the circle w4 that touches q1 internally while touching q2 and q3 externally:
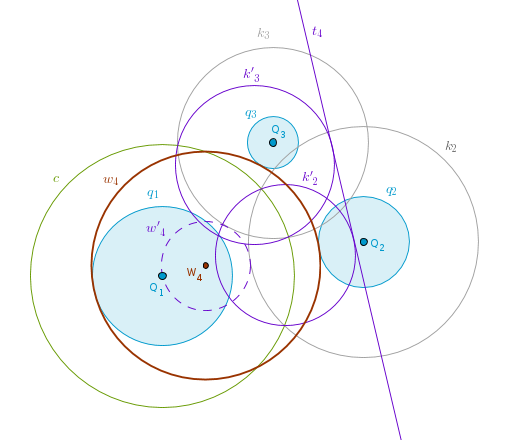
That is two extra solution circles for a total of four. If you repeat the above process for the remaining two circles, q2 and q3, you will construct the remaining 2 + 2 = 4 circles for a total of eight.
|
|
 IP Logged IP Logged |
|
|
|
rloginunix
Uberpuzzler
    

Posts: 1029
|
 |
Re: Inversion Tutorial. Part 2.
« Reply #5 on: Sep 13th, 2014, 2:02pm » |
 Quote Quote  Modify Modify
|
Orthogonal Circles.
Problem 5. Construct a circle which is orthogonal to a given circle q(Q, R) and passes through a given point P.
We already know how to solve this problem - ICP27.
Problem 6. Construct a circle which is orthogonal to two given non-concentric circles q1(Q1, R1) and q2(Q2, R2) and passes through a given point P.
Let us consider three cases: the given circles 1). are not in contact, 2). touch at T, 3). intersect at F1 and F2.
Case 1). The given circles are not in contact.
The solution follows directly from ICP27:
1). Invert P with respect to q1 to obtain P'1.
2). Invert P with respect to q2 to obtain P'2.
3). Construct a circle w which passes through three given points P, P'1, P'2:
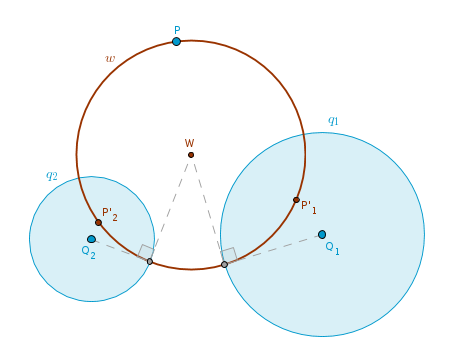
Case 2). The given circles touch at T.
Let us assume that the given circles touch externally. If P == T then the problem has an infinite number of solutions. Any circle with a center on a common tangent passing through T will be orthogonal to q1 and q2.
If P != T then inverting q1 and q2 with respect to c(T, TP) will transform them into parallel lines q'1 and q'2 (ICP22) while P will remain fixed. The solution then must be either a straight line or a circle - passing through P and orthogonal to two parallel straight lines. And since it can not be a circle it must be a straight line w' passing through a given point perpendicular to two parallel straight lines - a unique solution. Invert the straight line w' with respect to c(T, TP) to obtain the circle sought after:
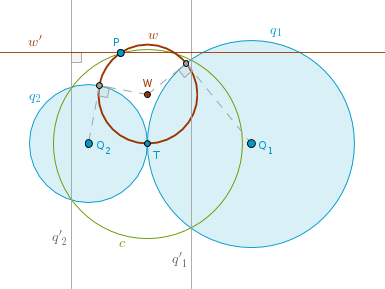
1). Invert q1 and q2 with respect to c(T, TP) to obtain the parallel straight lines q'1 and q'2.
2). Perpendicular w' to q'1 and q'2 through P.
3). Invert w' with respect to c(T, TP) to obtain the circle w sought after.
Case 3). The given circles intersect at F1 and F2.
If P == F1 (or P == F2) then a circle sought after exists only if the radius of one of the given circles is zero.
If P != F1 and P != F2 then inverting q1 and q2 with respect to c(F2, F2F1) will transform them into two distinct straight lines q'1 and q'2, each of which passes through F1 (ICP11), and inverting P with respect to c(F2, F2F1) will transform it into P'. The solution then must be either a straight line or a circle - passing through P' and orthogonal to two straight non-parallel lines. And since it can not be a straight line it must be a circle w'(F1, F1P') - a unique solution. Invert the circle w'(F1, F1P') with respect to c(F2, F2F1) to obtain the circle sought after:
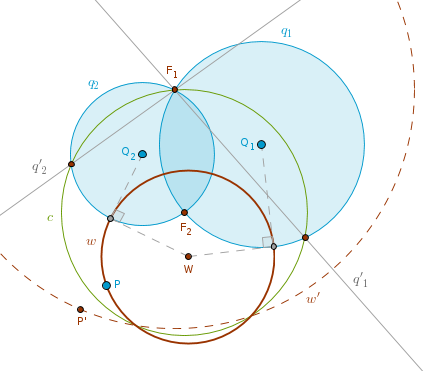
1). Invert q1 and q2 with respect to c(F2, F2F1) to obtain two distinct straight lines q'1 and q'2 intersecting at F1.
2). Invert P with respect to c(F2, F2F1) to obtain P'.
3). Circle(F1, F1P').
4). Invert Circle(F1, F1P') with respect to c(F2, F2F1) to obtain the circle w sought after.
|
|
 IP Logged IP Logged |
|
|
|
rmsgrey
Uberpuzzler
    

    
Gender: 
Posts: 2873
|
 |
Re: Inversion Tutorial. Part 2.
« Reply #6 on: Sep 14th, 2014, 8:09am » |
 Quote Quote  Modify Modify
|
on Sep 13th, 2014, 8:50am, rloginunix wrote:Tangent Circles.
Problem 1. Construct all circles which are tangent to a given circle q(Q, R) and pass through a given point P. |
|
Your example solution appears to be missing an infinite number of circles which are both tangent to q(Q,R) and pass through P. Oh, and since the problem asks for the construction of an infinite number of circles, I'd argue that it's a poorly formed problem.
Every point on the circle, except possibly two, has a unique tangent circle that passes through P - proof: consider a point, X, on q(Q,R). As you move a point, Y, along the line QX, the family of circles, C(Y,|XY|) will sweep the entire plane except the tangent line to q(Q,R) at X (unless your plane includes the point at infinity, in which case the tangent will also be swept). So, with the possible exception of the points where the tangents to q(Q,R) through P touch the circle, every point on the circumference will have a tangent circle passing through P.
|
|
 IP Logged IP Logged |
|
|
|
rloginunix
Uberpuzzler
    

Posts: 1029
|
 |
Re: Inversion Tutorial. Part 2.
« Reply #7 on: Sep 14th, 2014, 10:26am » |
 Quote Quote  Modify Modify
|
Yes, rmsgrey. You are absolutely right. My bad (too much typing,  ). ).
I meant the opening problem to be short, sweet and simple - to demonstrate the mechanics of the algorithm. The steps at the end of the problem begin with "1). Line(P, Q)" as that's what I had in my mind all along and thought that I have tightened the problem statement enough to avoid the infinity - apparently not. I will go back and fix it with "... and whose centers are located on the straight line passing through P and Q".
Thank you for helping me keep this tutorial in the best shape possible.
|
|
 IP Logged IP Logged |
|
|
|
rloginunix
Uberpuzzler
    

Posts: 1029
|
 |
Re: Inversion Tutorial. Part 2.
« Reply #8 on: Sep 21st, 2014, 12:09pm » |
 Quote Quote  Modify Modify
|
Problem 7. Find a circle of inversion with respect to which any two circles q1(Q1, R1) and q2(Q2, R2) that are not in contact can be inverted into two concentric circles.
Before we solve this problem we will need to get acquainted with two new concepts - a power of a point with respect to a circle and a radical axis.
A power of a point A with respect to a circle q(Q, r) is:
power(A, q) = d2 - r2
where d = AQ:
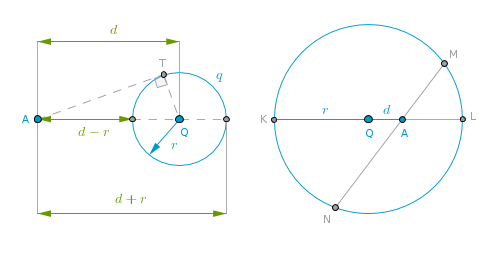
If A is located outside q then d > r and the above (positive) difference of squares can be rearranged as:
(d + r)*(d - r)
where (d + r) is the entire secant of q and (d - r) is its outer portion. If we construct a tangent to q through A (at T) then B3.P36 states that:
(d + r)(d - r) = AT2
In this case a power of a point A with respect to a circle q is the square of the length of the tangent to q through A.
If A is located on the circumference of q then d = r and the power of A with respect to q is zero. Lastly, if A is located inside q then d < r and the power of A with respect to q is negative:
power(A, q) = d2 - r2 = -(r2 - d2) = -(r + d)(r - d) = -AK*AL = -AM*AN
for any secant of q MN. This follows from B3.P35.
A radical axis of two circles q1 and q2 is a locus of points whose powers with respect to q1 and q2 are equal.
Instead of proving each of the upcoming cases separately it is easier to use one theorem to cover them all: a radical axis of any two nonconcentric circles is a straight line perpendicular to the straight line passing through the centers of these circles. To reduce the amount of new information I will omit the proof of this theorem at this point but if the audience insists I can always present it later.
From this theorem and the definition of a power of a point with respect to a circle it follows that the radical axis a of two circles that intersect at A and B is a straight line through A and B as the powers of both intersection points with respect to q1 and q2 are equal, zero, and two points define a unique straight line which is also perpendicular to Line(Q1, Q2).
If two circles touch at T externally or internally then the powers of T with respect to both circles are equal, zero. Hence, the radical axis must pass through T and it must be perpendicular to the straight line passing through the centers of the touching circles. In this case the radical axis a coincides with the tangent through T common to both circles.
There is more than one way to construct a radical axis a of two circles that are not in contact and are outside each other. One way would be to observe that in this particular case a power of a point with respect to a circle is the square of the length of a tangent through the point to the circle. Hence, we need to find a point the length of a tangent from which to both circles is the same. One such point, for example, is a middle point M of a common external tangent T1T2: MT1 = MT2. Constructing a straight line through M perpendicular to the straight line through the centers of both circles locates their radical axis a:
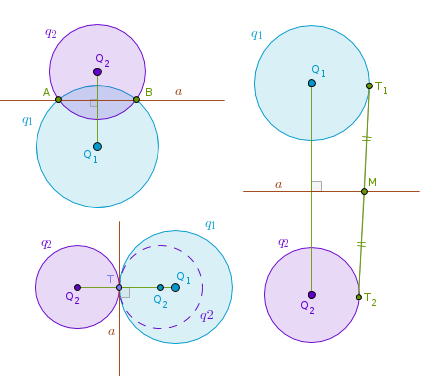
It is easier to construct the radical axis a of two nonconcentric circles that are not in contact and one is inside the other by using the method of intersecting loci. Here we employ the fact that a radical axis of two intersecting circles is a straight line passing through their intersection points.
Construct an arbitrary helper circle w1 that intersects both given circles and thus locates two pairs of intersection points. Then, a1 is a radical axis of q1 and w1 and a2 is a radical axis of q2 and w1. It stands to reason then that a1 and a2 intersect at a point P1 which must belong to a radical axis of q1 and q2.
Now either construct a second pair of intersecting radical axes (as I have done) or construct a straight line through P1 perpendicular to Line(Q1, Q2):
Note here that if a point on a radical axis has equal powers with respect to two circles then the squares of lengths of tangents through that point to both circles are also equal which means that the lengths of tangents themselves are equal and if they are equal they can play the role of radii. For a circle q(P, PT1 = PT2) thus constructed (see a sample configuration below) from the definition of power(P, q1) it follows that:
PS1*PS2 = PT21
And since that is true from B3.P37 it follows that PT1 is perpendicular to Q1T1 which means that q1 and q are orthogonal. By the same reasoning q2 and q are orthogonal:
It follows then that for any point on a radical axis there exists a unique circle orthogonal to both given circles. To construct such a circle choose a point on a radical axis, P, construct a tangent through P to one of the given circles to locate their tangency point T, draw Circle(P, PT). In other words a radical axis of two given circles is a locus of centers of circles orthogonal to both given circles.
It is also fairly obvious to observe and easy to prove that the converse statement is also true - the center of a circle q orthogonal to two given circles q1 and q2 must be located on the radical axis of q1 and q2.
|
|
 IP Logged IP Logged |
|
|
|
rloginunix
Uberpuzzler
    

Posts: 1029
|
 |
Re: Inversion Tutorial. Part 2.
« Reply #9 on: Sep 21st, 2014, 12:16pm » |
 Quote Quote  Modify Modify
|
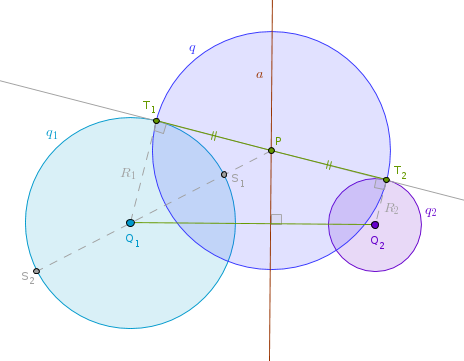
Back to our problem. Only two cases are possible here - the given circles are outside one another or one circle is inside the other. Let us look at the first case.
Without the loss of generality let us assume that between the two circles q1(O1, R1) and q2(O2, R2) R1 >= R2.
1). Line(Q1, Q2).
2). One external tangent t common to both circles touching q1 at T1 and q2 at T2.
3). Bisect LineSegment(T1, T2) to locate M: MT1 = MT2.
4). Perpendicular a to Line(Q1, Q2) through M to locate their intersection point Q.
5). Tangent to q1 through Q touching q1 at A.
6). Circle(Q, QA) until it intersects Line(Q1, Q2) at O1 and O2.
The point O1 is the center and LineSegment(O1, O2) is the radius of the inversion circle sought after:
The perpendicular a is the radical axis of q1 and q2 and as we have reasoned above the circle q is orthogonal to q1 and q2. It is also our choice to make Q, Q1, Q2 collinear.
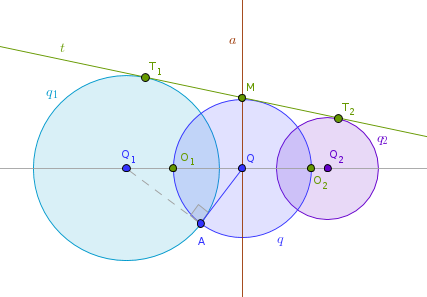
Under the inversion with respect to c(O1, O1O2) Line(Q1, Q2) inverts into itself as it passes through O1.
Since q passes through O1 and touches c at O2 it inverts into a straight line q' through O2 perpendicular to Line(Q1, Q2).
Since neither q1 nor q2 pass through the center of inversion their images under the inversion with respect to c will be circles q'1 and q'2. From ICP18 it follows that the centers of q'1 and q'2 must be collinear and, hence, must be located somewhere on Line(Q1, Q2).
But we know that inversion preserves angles so if q is orthogonal to q1 and q2 then its image, q', must also be orthogonal to q'1 and q'2. Since q' is a straight line and q'1 and q'2 are circles their centers must be somewhere on q'. The only location that satisfies both requirements at once is the intersection of Line(Q1, Q2) and q' - the point O2. Which, in turn, means that q'1 and q'2 are concentric:
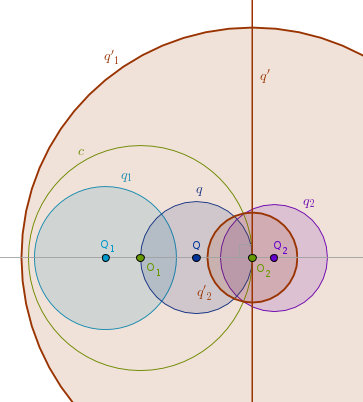
The remaining case when one circle is inside the other is solved in a similar way.
|
|
 IP Logged IP Logged |
|
|
|
rloginunix
Uberpuzzler
    

Posts: 1029
|
 |
Re: Inversion Tutorial. Part 2.
« Reply #10 on: Sep 21st, 2014, 12:41pm » |
 Quote Quote  Modify Modify
|
Mixed Problems.
Problem 8. Pappus Chain. Given two circles q1(Q1, R1) and q2(Q2, R2) (R1 > R2) that touch internally at T inscribe circles in the space between q1 and q2 in such a way that each inscribed circle touches two of its neighbors while touching q1 and q2.
Express the distance from the center of the n-th such circle to the line l through the centers of q1 and q2 in terms of its radius rn and n.
Choose T as a center of and 2*R1 as a radius of inversion. Under the inversion with respect to c(T, 2*R1) the given circles q1 and q2 become parallel straight lines q'1 and q'2 while the inscribed circles k0,k1, k2, ..., kn become the circles k'0,k'1, k'2, ..., k'n each of which has the same radius r'n (preservation of tangency points) so we might as well drop the index n and simply write it as r':
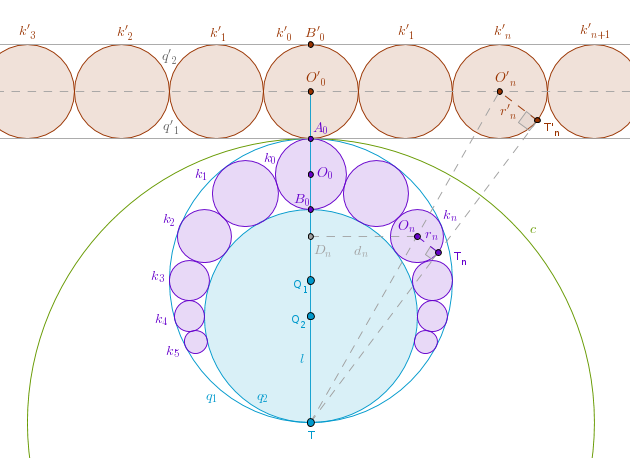
For the family of k' circles the solution is trivial:
O'0O'n = n * 2 * r'
d'n = 2nr' (where d'n = O'0O'n)
d'n/r' = 2n
Now we need to tie d'n and r' to dn and rn.
The triangles TDnOn and TO'0O'n are right by construction and share a common angle at T. By AAA they are similar and hence:
dn/TOn = d'n/TO'n
TOn/TO'n = dn/d'n
Under the inversion with respect to c a straight line through T tangent to kn at Tn will be transformed into itself while Tn will be carried into T'n. Since tangency points under inversion are preserved it follows then that Line(T, Tn) will also touch k'n at T'n.
Hence, the right triangles TOnTn and TO'nT'n, which share a common angle at T, are similar (AAA) and:
TOn/rn = TO'n/r'
TOn/TO'n = rn/r'
From the ratio established above it follows then that:
rn/r' = dn/d'n
rn/dn = r'/d'n = 2n
dn = 2nrn
Further, let us calculate the distance ln = TDn. From the right triangles TDnOn and TO'0O'n it follows that:
ln/dn = TO'0/O'0O'n = 2nr'
ln = (dn/(2n))*(TO'0/r')
But we already know that
dn/(2n) = rn
and so:
ln = rn*(TO'0/r')
Now we need to express TO'0 and r' via R1 and R2:
TO'0 = 2R1 + A0B'0/2 = 2R1 + (TB'0 - 2R1)/2 = R1 + TB'0/2
Since B'0 is the inverse of B0 with respect to c(T, 2R1):
TB'0*2R2 = 4R21
TB'0 = 2R21/R2
TO'0 = R1 + (1/2)*2R21/R2 = (R1/R2)*(R1 + R2)
r' = (1/2)*A0B'0 = (1/2)*(TB'0 - 2R1) = (R1/R2)*(R1 - R2)
ln = rn*(R1 + R2)/(R1 - R2)
[edit]
Typo fix: k' in "... will also touch k' at ..." became k'n.
[/edit]
|
| « Last Edit: Dec 30th, 2014, 11:15am by rloginunix » |
 IP Logged IP Logged |
|
|
|
rloginunix
Uberpuzzler
    

Posts: 1029
|
 |
Re: Inversion Tutorial. Part 2.
« Reply #11 on: Sep 29th, 2014, 4:43pm » |
 Quote Quote  Modify Modify
|
Lastly, let us express rn in terms of R1, R2 and n. From the similarity of the right triangles TOnTn and TO'nT'n it follows that:
rn/TTn = r'/TT'n
rn = r' * (TTn/TT'n)
Applying the ICC3 part of the definition of an inverse point to Tn and T'n we get:
TTn * TT'n = 4R21
TTn = 4R21/TT'n
and hence:
rn = r' * (4R21/TT'2n)
where r' is already known. To calculate TT'2n we recall that in this particular case it is a power of a point T with respect to k'n:
TT'2n = TO'2n - r'2
where TO'2n can be obtained via Pythagoras and the right triangle TO'0O'n:
TO'2n = TO'20 + 4n2r'2 (1)
Putting it altogether and simplifying (and sparing me a little bit from typing all the intermediate sup and sub tags) we get:
rn = ( 4R1R2*(R1 - R2) ) / ( (R1 + R2)2 + (4n2 - 1)*(R1 - R2)2 )
[edit]
Fixed the typo in (1), "n" became "n2".
[/edit]
|
| « Last Edit: Dec 26th, 2014, 7:07pm by rloginunix » |
 IP Logged IP Logged |
|
|
|
rloginunix
Uberpuzzler
    

Posts: 1029
|
 |
Re: Inversion Tutorial. Part 2.
« Reply #12 on: Sep 29th, 2014, 4:58pm » |
 Quote Quote  Modify Modify
|
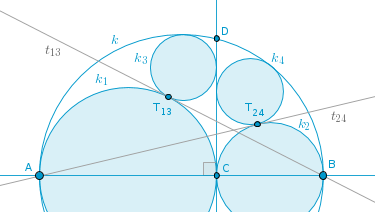
Problem 9. The Positive Negative Power or a Minus Plus Tango. Amongst the three given distinct collinear points A, B and C, the point C is located between the points A and B. Using the line segments AB, CA and CB as diameters three circles, k, k1 and k2, are constructed. Line(C, D) is perpendicular to Line(A, B). Each of the circles k3 and k4 touch k and Line(C, D) with k3 also touching k1 and k4 also touching k2.
Prove that:
9.1). the circles k3 and k4 are equal.
9.2). the tangent t13 common to k1 and k3 at T13 passes through B and the tangent t24 common to k2 and k4 at T24 passes through A:
Before we attempt to solve this problem let us observe that it is sometimes advantageous to alter a portion of the ICC2 definition just a bit. Instead of requiring that A and A' must be located on the same side of O let us see what will happen if we place O in between A and A' keeping the OA*OA' = r2 requirement intact:
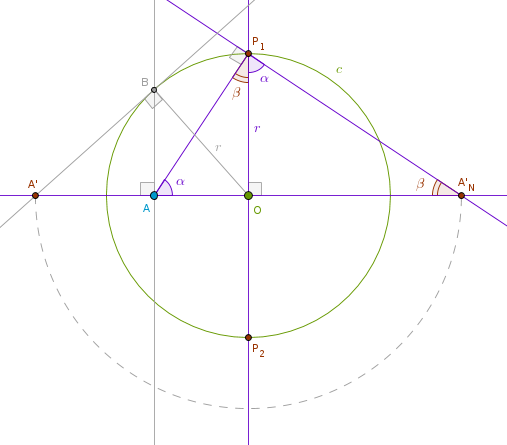
In this case instead of erecting a perpendicular to Line(O, A) through A we shall do so through O (note that I have highlighted the new construction steps in a different color). The perpendicular to Line(O, A) through O will intersect c(O, r) at P1 and P2 which are located diametrically opposite to each other. Construct LineSegment(A, P1). Construct a perpendicular to LineSegment(A, P1) at P1 until it intersects Line(O, A) at A'N.
As in Part 1 of this tutorial we can prove that the right triangles AP1A'N, AOP1 and P1OA'N are similar (AAA) and hence:
OA/r = r/OA'N
OA*OA'N = r2 = OA*OA'
where the rightmost part of the above equation is the inversion with respect to a circle we have studied in Part 1. We see that A'N is also an inverse of A with respect to c but of a different flavor - at the gut level "it is thrown on the other side of O". To distinguish between the two inversions (when needed) we can call the original one an inversion with respect to a circle with a positive power r2 and we can call this one an inversion with respect to a circle with a negative power -r2:
OA*OA'N = -r2
if we add the notion of signed line segments - to get to A' from O we have to move along Line(O, A) in one direction and to get to A'N from O we have to move along Line(O, A) in the opposite direction.
From the above equation, after OA cancels out, it follow that:
OA'N = *OA'
which means that to obtain A'N we can use an inversion with a positive power to obtain A' and then either reflect A' with respect to Line(P1, P2) or rotate A' about O 180 degrees. Since we can do it for an arbitrary point we can do it for a collection of them and hence an inversion with a negative power is equivalent to an inversion with a positive power with a consequent reflection or rotation.
It follows then that all the properties of an inversion with a positive power that we have studied in Part 1 also apply to an inversion with a negative power (where it makes sense) subject to reflection/rotation. If that does not sound convincing enough here is a sample proof of ICP9's equivalent, for example:

Since P belongs to c and the circumference angle PAP'N is right from B3.P31 it follows that P'N also belongs to c. Which means that under the inversion with a negative power every point on the circle of inversion is transformed into a diametrically opposite point on the (same) circle of inversion - such an inversion does not have fixed points at all, even though the circle of inversion is still transformed into itself.
Pick an arbitrary point B on l and invert it with a negative power into B'N. Consider the triangles OPB and OB'NP'N. From the above observations it follows that Line(B, B'N) and Line(P, P'N) pass through O. Hence the angles they form at O, angle BOP and angle B'NOP'N, are vertical and equal to each other (B1.P15).
From the definition of the inverse points it follows that:
OP*OP'N = OB*OB'N
which means that the above triangles have the sides about the equal angle in the same proportion and hence they are similar (B6.P6) and hence:
angle OPB = 90 degrees = OB'NP'N
And since the point B was chosen at random the locus traced by B'N must be a circumference of a circle with OP'N as diameter.
Another interesting feature of an inversion with a negative power that may come in handy is the following: any circle w that passes through two diametrically opposite points on another circle c is invariant under the inversion with respect to c with a negative power:
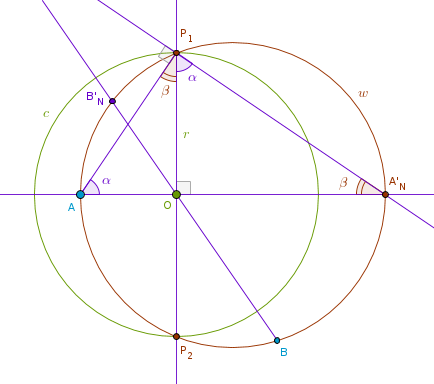
From the previous observations we already know that:
OA*OA'N = r2
Pick an arbitrary point B on w and construct Line(B, O) which will intersect w at B'N. Since B3.P35 applies to any intersecting chords of w:
OB*OB'N = OA*OA'N = r2
which means that B and B'N are images of each other under the inversion with respect to c with a negative power and hence w is invariant under that inversion.
Further, if we rewrite the above formula as:
OB'N = r2/OB
we see that the length of LineSegment(O, B'N) does not depend on a particular choice of w - if we fix these two points, B and B'N, we can then construct an infinite number of circles like w. We just have to make sure that these circles pass through two points diametrically opposite to each other on c, N1 and N2:
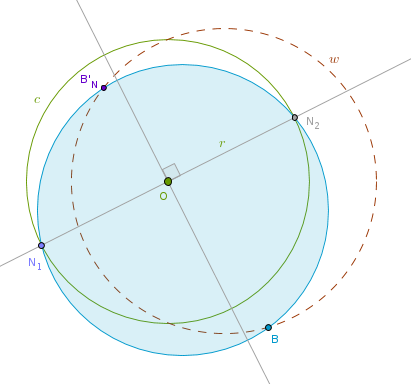
Here is a summary of popular inversions with a negative power:
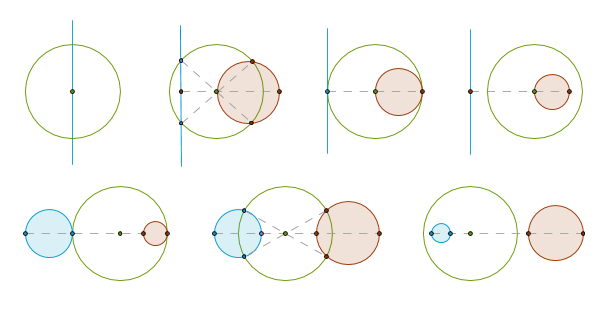
[edit]
"B P O" (w/o spaces) is rendered as ****. Changed "B P O" to "OPB".
[/edit]
|
| « Last Edit: Oct 26th, 2014, 1:23pm by rloginunix » |
 IP Logged IP Logged |
|
|
|
rloginunix
Uberpuzzler
    

Posts: 1029
|
 |
Re: Inversion Tutorial. Part 2.
« Reply #13 on: Sep 29th, 2014, 5:14pm » |
 Quote Quote  Modify Modify
|
Back to our problem.
9.1). The problem statement says that C is between A and B. So if we choose C to be the center of inversion with a negative power then we can require A and B to be the images of each other under that inversion. Since Line(C, D) is a given perpendicular to Line(A, B) finding the radius of this inversion is trivial: r == CD, so c == Circle(C, CD).
Under the inversion with respect to c with a negative power:
- Line(A, B) and Line(C, D) invert into themselves.
- k also inverts into itself as it passes through D and D', which are diametrically opposite to each other on c.
- k1 inverts into a straight line k'1 perpendicular to Line(A, B) and touching k at B, preservation of tangency points.
- k2 inverts into a straight line k'2 perpendicular to Line(A, B) and touching k at A, preservation of tangency points.
- k3 inverts into a circle k'3 touching Line(C, D), k and k'1, preservation of tangency points.
- k4 inverts into a circle k'4 touching Line(C, D), k and k'2, preservation of tangency points:
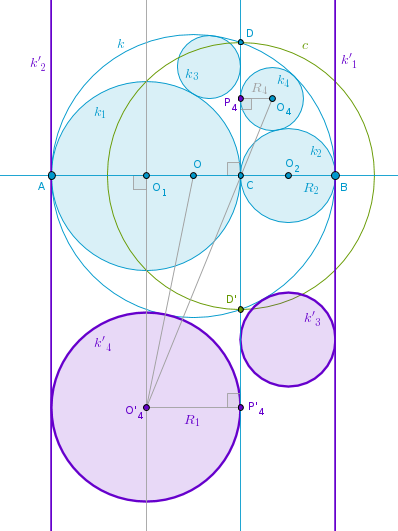
Let:
O1A = O1C = R1
O2C = O2B = R2
OA = OB = (2R1 + 2R2)/2 = R1 + R2 = R
Let us express the radii of k3, R3, and k4, R4, via R1 and R2 and prove that R3 == R4.
Consider the circles k4 and k'4. Line(C, D) is their common tangent. Points O4, C and O'4 are collinear. We can easily prove that the right triangles CP4O4 and CP'4O'4 are similar and:
R4/CP4 = R1/CP'4
R4 = R1 * (CP4/CP'4)
Since P4 and P'4 are inverses of each other with respect to c:
CP4*CP'4 = CD2
CP4 = CD2/CP'4
Putting CP4 back into the formula for R4 we get:
R4 = R1 * (CD2/CP'24)
Since A and B are inverses of each other with respect to c:
CA*CB = CD2 = 4R1R2
To find CP'24 we use Pythagoras and the right triangle OO1O'4:
CP'24 = O1O'24 = OO'24 - OO21 = (2R1 + R2)2 - (R1 + R2 - R1)2 = 4R1(R1 + R2)
And hence:
R4 = R1 * (4R1R2/4R1(R1 + R2) = R1R2/(R1 + R2)
In a similar way we can show that:
R3 = R1R2/(R1 + R2)
and hence R3 == R4.
9.2). This time we choose B as a center of inversion with a positive power and require that C and A must be the images of each other under that inversion. We can use ICE2 (from Part 1) to find r - Line(C, D) is a perpendicular to Line( A, B) through C so c == Circle(B, BD).
Under that inversion:
- Line(A, B) inverts into itself.
- Line(C, D) inverts into k.
- k inverts into Line(C, D).
- k1 passes through A and C, hence it is orthogonal to c and it inverts into itself (ICP27).
- k3 touches k, k1 and Line(C, D) all of which invert into their original configuration. And since inversion preserves tangency points k3 must invert into itself and it also must be orthogonal to c:
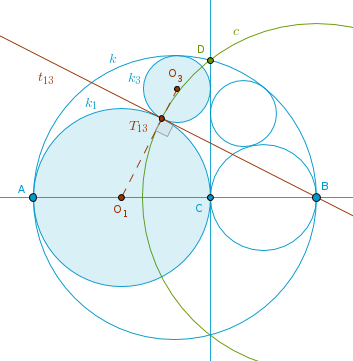
It follows then that T13 - the (single) point of tangency of k1 and k3 - will also invert into itself. It will remain where it is, fixed, and hence it must be on c (inversion with a positive power).
But c cuts the AT13C semi-circle portion of k1 in only one (fixed) point. So in fact T13 belongs to three circles at once, c, k1, k3, two of which, k1 and k3, touch and are orthogonal to the third one, c. From the definition of orthogonal circles it follows then that the tangent t13 common to k1 and k3 at T13 must pass through B.
The case of t24 is proved in the similar way - choose A as a center of inversion with a positive power, make C and B inverses of each other under that inversion and so on.
|
|
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register