Author |
Topic: Neat problem from the Maryland Math Olympiad (Read 1873 times) |
|
amichail
Senior Riddler
Posts: 450
|
 |
Neat problem from the Maryland Math Olympiad
« on: Dec 8th, 2007, 3:09pm » |
 Quote  Modify
|
Each point in the plane is colored either red or green. Let ABC be a fixed triangle. Prove that there is a triangle DEF in the plane such that DEF is similar to ABC and the vertices of DEF all have the same color.
|
| « Last Edit: Dec 8th, 2007, 3:12pm by amichail » |
 IP Logged |
DropZap - a new kind of block elimination game
|
|
|
Aryabhatta
Uberpuzzler
Gender: 
Posts: 1321
|
I think this has appeared before when ABC is equilateral...
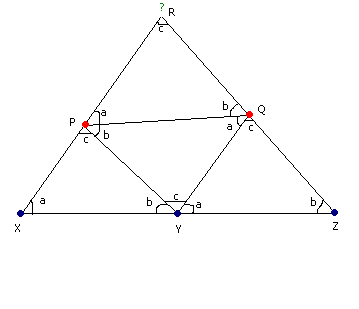
Anyway, i guess the figure below does not give away much, so not zipping it.
First we can show that there are three collinear points XYZ such that |XY| = |YZ| (Y is midpoint of XZ) and that X,Y,Z are all coloured the same colour (say blue).
Suppose the angles of ABC are a, b and c.
Now consider the below figure.
Each of the triangles XYP, QYZ, PQR and XZR are similar to ABC.
Now assume there is no triangle similar to ABC with like coloured vertices.
Then from XYP , P is red. Similarly Q is Red.
By considering PQR, R must be blue, but by considering XZR, R must be red...
Thus we see that there must be at least one.
This problem is no different from the one in which a=b=c=60 (an old IMO problem).
I believe Medium is probably the right forum for this.
|
|
IP Logged |
|
|
|
amichail
Senior Riddler
Posts: 450
|
|
Re: Neat problem from the Maryland Math Olympiad
« Reply #2 on: Dec 8th, 2007, 7:07pm » |
Quote Modify
|
on Dec 8th, 2007, 6:01pm, Aryabhatta wrote:
First we can show that there are three collinear points XYZ such that |XY| = |YZ| (Y is midpoint of XZ) and that X,Y,Z are all coloured the same colour (say blue).
|
|
How would someone come up with this observation? What made you think of it?
|
|
IP Logged |
DropZap - a new kind of block elimination game
|
|
|
Aryabhatta
Uberpuzzler
Gender:
Posts: 1321
|
|
Re: Neat problem from the Maryland Math Olympiad
« Reply #3 on: Dec 8th, 2007, 7:54pm » |
Quote Modify
|
on Dec 8th, 2007, 7:07pm, amichail wrote:
How would someone come up with this observation? What made you think of it? |
|
Not sure if there is a systematic method... but this one came up when solving the case when ABC is equilateral and that was long ago.
I think this was the line of thought (hidden in case of spoilers):
Try to get a configuration of equilateral triangles which gives us many triangles with common vertices. The first configuration which came to mind was the triangle and midpoints.
Then trying to look at random colours sort of led nowhere, so a "what if" question arose: what if the colours of a side were the same. This led to the midpoint issue which can be shown easily and the equilateral triangle issue was resolved soon.
|
|
IP Logged |
|
|
|
ecoist
Senior Riddler
Gender:
Posts: 405
|
|
Re: Neat problem from the Maryland Math Olympiad
« Reply #4 on: Dec 9th, 2007, 10:00am » |
Quote Modify
|
I agree with Aryabhatta that this problem is not suitable for hard. However, I disagree that this problem is the same as the one in which the given triangle is equilateral. In that special case, one does not need three collinear points equally spaced and monochromatic to show the existence of a monochromatic equilateral triangle. Aryabhatta omits a proof of the existence of three collinear points equally spaced and monochromatic. Doesn't seem obvious to me. For example, is the puzzle below obvious?
Color the integers 1,2,...,9 red or green. Show that there must exist three of these integers, a<b<c, such that all three have the same color and b=(a+c)/2.
|
| « Last Edit: Dec 9th, 2007, 10:44am by ecoist » |
IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: Neat problem from the Maryland Math Olympiad
« Reply #5 on: Dec 9th, 2007, 10:30am » |
Quote Modify
|
on Dec 9th, 2007, 10:00am, ecoist wrote:For example, is the puzzle below obvious?
Color the integers 1,2,...,8 red or green. Show that there must exist three of these integers, a<b<c, such that all three have the same color and b=(a+c)/2. |
|
Trick question? Because it doesn't seem to hold for RRGGRRGG
|
|
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
ecoist
Senior Riddler
Gender:
Posts: 405
|
|
Re: Neat problem from the Maryland Math Olympiad
« Reply #6 on: Dec 9th, 2007, 10:41am » |
Quote Modify
|
Right, towr! Just noticed my error! Changing 8 to 9.
|
|
IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: Neat problem from the Maryland Math Olympiad
« Reply #7 on: Dec 9th, 2007, 10:48am » |
Quote Modify
|
Well, then it's easy enough to verify; but not blatantly obvious.
|
|
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Aryabhatta
Uberpuzzler
Gender:
Posts: 1321
|
|
Re: Neat problem from the Maryland Math Olympiad
« Reply #8 on: Dec 9th, 2007, 11:01am » |
Quote Modify
|
on Dec 9th, 2007, 10:00am, ecoist wrote:I agree with Aryabhatta that this problem is not suitable for hard. However, I disagree that this problem is the same as the one in which the given triangle is equilateral. In that special case, one does not need three collinear points equally spaced and monochromatic to show the existence of a monochromatic equilateral triangle. Aryabhatta omits a proof of the existence of three collinear points equally spaced and monochromatic. Doesn't seem obvious to me. For example, is the puzzle below obvious?
<snip nice problem>
|
|
By same I meant similar in "hardness" level, i.e. medium. I didn't mean mathematically equivalent, though I think we might be able to show that if this propertly is true for equilateral, then it is true for arbitrary triangles by some kind of transformation of the plane.
As to the equidistant points of same colour, I left the proof because of laziness and I agree it is not obvious, but it is not very hard either.
|
|
IP Logged |
|
|
|
ecoist
Senior Riddler
Gender:
Posts: 405
|
|
Re: Neat problem from the Maryland Math Olympiad
« Reply #9 on: Dec 9th, 2007, 11:09am » |
Quote Modify
|
Yes, towr. Process of elimination is sufficient, though it can be tedious. Works for amichail's problem too, except, without Aryabhatta's clever setup, one might give up before elimination yields any result! Elimination works rather quickly if the triangle is equilateral.
|
| « Last Edit: Dec 9th, 2007, 11:17am by ecoist » |
IP Logged |
|
|
|
FiBsTeR
Senior Riddler
Gender:
Posts: 581
|
|
Re: Neat problem from the Maryland Math Olympiad
« Reply #10 on: Dec 9th, 2007, 12:16pm » |
Quote Modify
|
on Dec 9th, 2007, 10:00am, ecoist wrote:| Color the integers 1,2,...,9 red or green. Show that there must exist three of these integers, a<b<c, such that all three have the same color and b=(a+c)/2. |
|
This was problem 1 on Round 2 of the USAMTS this year, which I'm glad to say I got right.
|
|
IP Logged |
|
|
|
Hippo
Uberpuzzler
Gender:
Posts: 919
|
|
Re: Neat problem from the Maryland Math Olympiad
« Reply #11 on: Dec 9th, 2007, 12:51pm » |
Quote Modify
|
OK, it's easy forcing: Suppose there exists such coloring ... suppose there are at least 2 numbers of each color 
Let 0 is WLOG blue. Let a be another blue number. Than -a is red as so as 2a is red. Therefore -4a is blue.
Now 4a and 6a should be red (-4a,0);(-4a,a), and we got 2a,4a,6a red ... contradiction.
|
|
IP Logged |
|
|
|
ecoist
Senior Riddler
Gender:
Posts: 405
|
|
Re: Neat problem from the Maryland Math Olympiad
« Reply #12 on: Dec 9th, 2007, 2:42pm » |
Quote Modify
|
Quote:| By same I meant similar in "hardness" level, i.e. medium. I didn't mean mathematically equivalent, though I think we might be able to show that if this propertly is true for equilateral, then it is true for arbitrary triangles by some kind of transformation of the plane. |
|
Examining your figure, Aryabhatta, let S be the point where PQ extended meets the line through Z parallel to YQ. Then triangle QSZ is similar to triangle PRQ. If triangle PRQ is equilateral, then triangle YRS is equilateral. If triangle PRQ is not equilateral, triangle YRS need not be similar to PRQ. Hence nonsingular linear transformations of the equilateral triangular grid map some similar triangles into dis-similar triangles. Since the equilateral triangular grid contains similar equilateral triangles with infinitely many different orientations, I don't think it's possible to choose a transformation that preserves similarity of triangles.
|
|
IP Logged |
|
|
|
Aryabhatta
Uberpuzzler
Gender:
Posts: 1321
|
|
Re: Neat problem from the Maryland Math Olympiad
« Reply #13 on: Dec 9th, 2007, 5:39pm » |
Quote Modify
|
on Dec 9th, 2007, 2:42pm, ecoist wrote:
Examining your figure, Aryabhatta, let S be the point where PQ extended meets the line through Z parallel to YQ. Then triangle QSZ is similar to triangle PRQ. If triangle PRQ is equilateral, then triangle YRS is equilateral. If triangle PRQ is not equilateral, triangle YRS need not be similar to PRQ. Hence nonsingular linear transformations of the equilateral triangular grid map some similar triangles into dis-similar triangles. Since the equilateral triangular grid contains similar equilateral triangles with infinitely many different orientations, I don't think it's possible to choose a transformation that preserves similarity of triangles. |
|
We actually don't need the transformation to cater to all possible orientations, as we can show that there is some monochromatic equilateral triangle with one of its sides parallel to a given line.
|
|
IP Logged |
|
|
|
ecoist
Senior Riddler
Gender:
Posts: 405
|
|
Re: Neat problem from the Maryland Math Olympiad
« Reply #14 on: Dec 9th, 2007, 7:30pm » |
Quote Modify
|
Quote:| We actually don't need the transformation to cater to all possible orientations, as we can show that there is some monochromatic equilateral triangle with one of its sides parallel to a given line. |
|
Of course! Your proof confirms this. My (clumsily presented) point is simply that there is an easier proof for an equilateral triangle, which fails to work for an arbitrary triangle. Thus, some things are lost by transforming, undermining your comment
Quote:| I think we might be able to show that if this propertly is true for equilateral, then it is true for arbitrary triangles by some kind of transformation of the plane. |
|
|
|
IP Logged |
|
|
|
rmsgrey
Uberpuzzler
    
Gender:
Posts: 2872
|
|
Re: Neat problem from the Maryland Math Olympiad
« Reply #15 on: Dec 11th, 2007, 6:55am » |
Quote Modify
|
on Dec 9th, 2007, 12:51pm, Hippo wrote:OK, it's easy forcing: Suppose there exists such coloring ... suppose there are at least 2 numbers of each color
Let 0 is WLOG blue. Let a be another blue number. Than -a is red as so as 2a is red. Therefore -4a is blue.
Now 4a and 6a should be red (-4a,0);(-4a,a), and we got 2a,4a,6a red ... contradiction. |
|
There's a simpler proof for arbitrary points on a line - start with any two points of the same colour: 0 and 2a, then they form triples with -2a, a and 4a, which are themselves a triple.
As for integers 1-9:
Looking at 34567, if any of the pairs 3,5 4,6 or 5,7 are two of the same colour, then you can use that pair as 0 and 2a in the above argument. If not, then they must be in the pattern ..XXYYX.. (or the reverse, which is equivalent) so 1 and 2 must both be Y (4,7 and 3,4 respectively) giving YYXXYYX.. 8 must be X (2,5) and then 9 can be neither X nor Y (1,5 and 7,
|
|
IP Logged |
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print