Author |
Topic: Circles and straights (Read 7664 times) |
|
Altamira_64
Junior Member
Posts: 116
|
 |
Circles and straights
« on: Jul 22nd, 2013, 7:16am » |
 Quote  Modify
|
Start by drawing 4 points, not belonging on the same straight line or same circle. We are looking for the number of straight lines and circles which are equidistant from these 4 points. (The distance of a point P from a circle with center C is the straight PA, where A is the node of the straight PC with the circle circumference).
|
|
 IP Logged |
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
Gender: 
Posts: 7526
|
|
Re: Circles and straights
« Reply #1 on: Jul 22nd, 2013, 9:07am » |
Quote Modify
|
If I am not mistaken there should be 7 solutions.
|
|
IP Logged |
|
|
|
antkor
Newbie
Posts: 30
|
|
Re: Circles and straights
« Reply #2 on: Nov 24th, 2013, 5:15pm » |
Quote Modify
|
could you explain how did you find that out?
|
|
IP Logged |
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 7526
|
|
Re: Circles and straights
« Reply #3 on: Nov 30th, 2013, 3:43am » |
Quote Modify
|
There are 7 ways to split the points in 2 groups. Experimentally, it seems that for each of them, there is exactly one solution where each group is on one side of the line or circle.
There is at least one special case where it doesn't work, it is the case where all 4 points lie on the same line or circle. In that case, there is an infinity of solutions.
|
|
IP Logged |
|
|
|
rloginunix
Uberpuzzler
Posts: 1029
|
|
Re: Circles and straights
« Reply #4 on: Dec 13th, 2013, 7:35pm » |
Quote Modify
|
This problem can be generalized by adding one dimension to it. Replace non-collinear with non-coplanar and lines and circles with planes and spheres:
how many planes and spheres equidistant from four non-coplanar points can be constructed?
Before I discuss its solution though a quick look at 3 and 4-point 2D cases.
|
|
IP Logged |
|
|
|
rloginunix
Uberpuzzler
Posts: 1029
|
|
Re: Circles and straights
« Reply #5 on: Dec 13th, 2013, 7:51pm » |
Quote Modify
|
3 points.
One way to solve this problem is by using the Scope Reduction approach - keep reducing the scope of the problem until you hit rock bottom and come across a problem you can solve. Find some good patterns. Step up and bring these patterns with you. And up, and up and up until you clime your way out of the hole.
A curious bear may ask how the hell did you, smart as., know to use this particular approach to begin with? Why not some other one? You got me. On and off I've been thinking about this for a while without much success.
1-point case doesn't make sense. While working on the 2-point case yourself you found two patterns that run through the entire problem - combinatorial and geometric. Combinatorial pattern - grouping the points relative to the curve. Geometric pattern - splitting the spatial difference in half, playing a little Euclid along the way assuming that it doesn't exist until you construct it.
I found it convenient to refer to both lines and circles as just the Curve. Incidentally both have constant curvature. Zero for straight lines, one over radius for circles.
Combinatorics. If you place all three distinct points A, B and C on one side of the Curve then to satisfy the requirement of equidistance they would have to sit on a similar curve - straight line for straight lines and circle for circles. This is a degenerate condition excluded by the problem's definition. Consequently you have to mix the points up. There are three ways to do that:
A BC
B AC
C AB
Geometry. To construct the required curve you would use your 2-point finds - splitting the spacial difference. For example, A on one side of the curve and B and C on the other. Treat two points B and C as just one and split the distance between A and one aggregate point in two. For that to work the aggregate point BC has to sit on the similar curve. It should be on the straight line for straight lines and circle for circles.
Straight line:
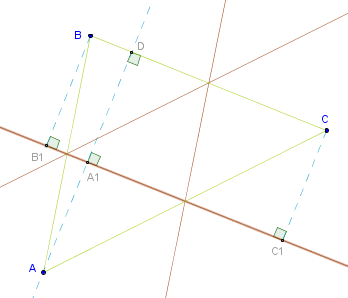
1). Line through B and C (L(B, C)).
2). Perpendicular to L(B, C) through A locates D.
3). Bisect AD to construct a line equidistant from A, B and C: AA1 = BB1 = CC1.
So in 2D you can only construct three such lines. In 3D the number of lines equidistant from three points is infinite.
Circles.
A circle can be constructed through any three non-collinear points. So here the problem breaks down a little bit. Triangle's circumcenter is the center of an infinite number of circles equidistant from three points whether these points are all in or outside the circle. Here AD1 = BD2 = CD3 and AE1 = BE2 = CE3:
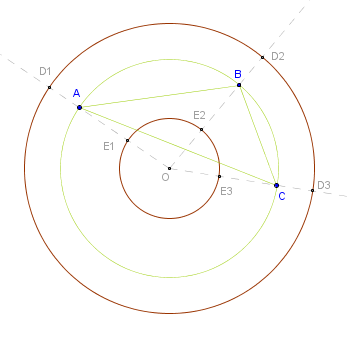
Another set of infinite number of circles equidistant from three points can be found by using our pattern of splitting the spatial difference between A and an aggregate point BC. In this case the aggregate must be on a circle. A set of points equidistant from two given ones is its bisector. So:
1). Bisect the line segment BC.
2). Pick any point O on the bisector.
3). Construct a circle centered at O with radius OB = OC.
4). Connect A with O. That line will intersect the circle at D.
5). Whether A is in or outside the circle bisect AD to get E.
6). Construct a circle centered at O with radius OE.
[edit]
Moved the drawing files to this forum.
[/edit]
|
| « Last Edit: Apr 5th, 2014, 8:04am by rloginunix » |
IP Logged |
|
|
|
rloginunix
Uberpuzzler
Posts: 1029
|
|
Re: Circles and straights
« Reply #6 on: Dec 13th, 2013, 8:05pm » |
Quote Modify
|
4 points.
Bring your 2 and 3-points finds.
Combinatorics. If you place all four distinct points on one side of the Curve they would have to sit on the similar curve. Degenerate case. Throw it out. Start grouping the points relative to the side of the Curve they are on. Your only choices are 1 + 3 and 2 + 2.
Since the order of items doesn't matter we have four 1 + 3 cases:
A BCD
B ACD
C ABD
D ABC
and three 2 + 2 cases:
AB CD
AC BD
AD BC
Geometry. Circles. 1 + 3. A is outside and B, C and D are inside. Treat all three points as one aggregate and split the distance between A and it in two. Hug three points with a circle, snap a line to A, cut the distance in half, circle is done:
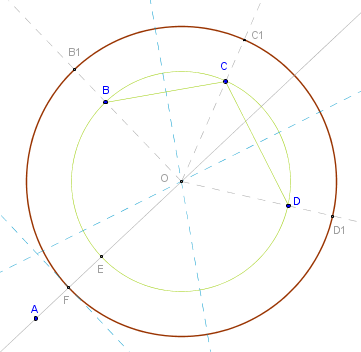
1). Construct a 3-point B, C, D circle.
2). Connect A with O.
3). That line will intersect the circle at E.
4). Bisect AE.
5). Construct the final circle centered at O with radius OF.
Four circles total - this one plus B outside, C outside, D outside.
2 + 2. Split the distance between the two aggregates in half. A set of points equidistant from two points is the bisector. Intersection of two bisectors is a point equidistant from all four points:
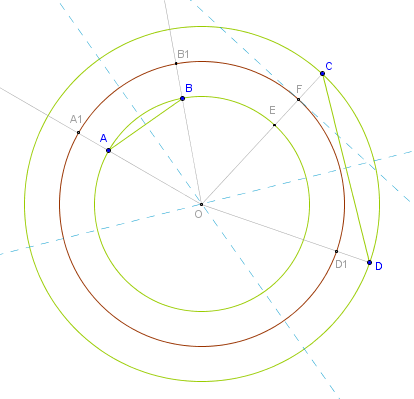
1). Construct two circles centered at bisectors intersection O.
2). Snap a line OC from common center through both circles.
3). That line will cut one circle at E.
4). Bisect CE to locate F.
5). Construct a circle centered at O with radius OF: AA1 = BB1 = CF = DD1.
So if bisectors intersect it's three more circles. 3 + 4 = 7 circles total.
Straight line.
2 + 2. If bisectors do not intersect then they are parallel. No banana for you you naughty circle. Here's a nice banana for you straight line. These four points sit on two parallel lines so the line equidistant from both runs half way between them. For a total of three straight lines. If 2 + 2 bisectors do intersect then no banana for straight lines.
1 + 3. All three points as an aggregate must sit on a straight line. Snap a perpendicular from the fourth point on to a line, bisector of that perpendicular is the line equidistant from all four points. Four total. 3 + 4 = 7 straight lines altogether.
[edit]
Moved the drawing files to this forum.
[/edit]
|
| « Last Edit: Apr 5th, 2014, 8:06am by rloginunix » |
IP Logged |
|
|
|
rloginunix
Uberpuzzler
Posts: 1029
|
|
Re: Circles and straights
« Reply #7 on: Dec 13th, 2013, 8:19pm » |
Quote Modify
|
Generalized problem.
Warning - complete solution coming right up. If you want to swing it on your own - don't read.
How many planes and spheres equidistant from four non-coplanar points can be constructed?
Planes.
If you did all the previous cases this one should be a piece of cake. The answer is also seven. To visualize the situation a little bit better treat the given points as vertexes of a tetrahedron. Then they can be grouped in two ways as 1 + 3 and 2 + 2 relative to the equidistant plane. By now we know that the first group has four choices and the second only three for a total of seven.
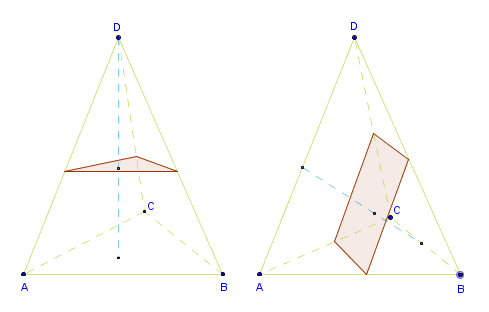
In the sketch I've shown just one case for each grouping. For the 1 + 3 case (on the left) the equidistant plane is positioned half way through the tetrahedron's height parallel to the 3 points plane.
For the 2 + 2 case (on the right) the equidistant plane is constructed through the middles of the edges connecting the opposite points. As such it sits half way between the edges of the tetrahedron that cross over in space. This is important because if the edges do not cross over in space - are parallel - then there's no unique plane and you could construct and infinite number of them.
If the edges do cross over then they locate a unique plane constructed thus. Construct a line through B parallel to AD. You will have two non-parallel lines BC and BB1 that locate a unique plane. Do the same with AD. Construct a line through A parallel to BC. You will have two lines AD and AA1 that locate a unique plane. Snap a perpendicular between these two planes at any point. Bisect the perpendicular with a plane which will be equidistant from all four points.
In the sketch the edges that cross over in space are AD and BC.
Spheres.
Spheres are not that interesting because the answer is lemniscate of Gerono. Just kidding. Infinite amount.
1 + 3. Three non-collinear points A, B and C form a triangle in a plane. Its circumcenter O is a point equidistant from all three points. Construct a line through O perpendicular to the ABC's plane. That line is a set of all points equidistant from A, B and C in 3D. So we can have an infinite number of spheres kissing all three points as long as sphere's center is on that line. Let's pick just one. Connect the center of such sphere O with the fourth point D. That line will intersect the sphere at a point E. Cut ED in half at F (EF = FD) with a plane perpendicular to ED and parallel to the plane tangent to the sphere at E and construct a new sphere centered at O with radius OF.
2 + 2. Connect say A and B with a line. Bisect that line with a plane. That plane will be a set of all points equidistant from A and B. All the spheres centered on that plane with the radius OA = OB will kiss A and B. Same for D and C. These two planes don't have to intersect but when they do they will produce a line - a set of points in 3D equally distanced from A, B, C and D. Pick just one - O. Construct two spheres centered at O. Construct a ray from O intersecting both spheres at points E and F. Construct tangent planes to both spheres at E and F, bisect EF with a plane parallel to tangent planes, get a half way point G, construct the sphere centered at O with radius OG, etc, etc.
[edit]
typo, fixed OA = AB in the last paragraph to read OA = OB. Moved the drawing file to this forum.
[/edit]
|
| « Last Edit: Apr 5th, 2014, 8:09am by rloginunix » |
IP Logged |
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print