Author |
Topic: Brocard Point(s). (Read 3850 times) |
|
rloginunix
Uberpuzzler
Posts: 1029
|
 |
Brocard Point(s).
« on: May 17th, 2014, 10:33am » |
 Quote  Modify
|
Brocard Point(s).
This is the second problem of the 1895 Hungarian Math Competition from the "Hungarian Problem Book I, based on the Eotvos Competitions, 1894-1905" book, ISBN 0-88385-611-5, page 9 (of the paperback Eighth Printing edition that I have):
Construct a point N inside an arbitrary right triangle ABC such that all three angles NBC, NCA and NAB are equal.
After you solve the problem for a right triangle generalize your solution for any triangle. By doing so you will discover an algorithm to locate two points inside an arbitrary triangle named after the French mathematician and meteorologist Henri Brocard (1845-1922).
|
|
 IP Logged |
|
|
|
jollytall
Senior Riddler
Gender: 
Posts: 585
|
|
Re: Brocard Point(s).
« Reply #1 on: May 19th, 2014, 11:37am » |
Quote Modify
|
For the right angle version. Let ABC=90.
NAB=NBC=NCA, but also NBA+NBC=90, or NBA=90-NBC=90-NAB. Hence ANB=90. From Thales, we know that N is on the circle drawn on AB.
Let take B' on AB mirroring B on A.
B'AC+CAN+NAB=180, but because NAB=NCA, B'AC+CAN+NCA=180.
From a the ANC triangle we know that ANC+CAN+NCA=180.
B'AC=ANC.
Now, if we draw a circle with the AC distance from B', we get a D point on AC. We have B'D=AC and B'AD=ANC. So, by drawing a circle around A with the distance AB and another one around C with AD then they cross each other in E (taking the one on the same side of AC where B is). AEC triangle is the same as B'AD triangle, so B'AC=ANC=AEC. If we draw the circle around the AEC triangle then N will be on it too.
So the crossing point of this last and the first circles is N.
There are two such points if not NAB=NBC=NCA, but the other way round NBA=NCB=NAC.
|
|
IP Logged |
|
|
|
jollytall
Senior Riddler
Gender:
Posts: 585
|
|
Re: Brocard Point(s).
« Reply #2 on: May 19th, 2014, 12:55pm » |
Quote Modify
|
My son has just pointed out two things:
In the second circle it is easier to get to E (another E with the same purpose) by drawing the half of CAB on AC, both from A and C. Then AEC=ANC, etc.
For all the inner xNy angles it is true to be xNy=180-xyz. This is why the first circle was 90 degrees Thales. But then it is true for non-right-angle solutions, so it is also the general solution.
|
|
IP Logged |
|
|
|
rloginunix
Uberpuzzler
Posts: 1029
|
|
Re: Brocard Point(s).
« Reply #3 on: May 19th, 2014, 11:09pm » |
Quote Modify
|
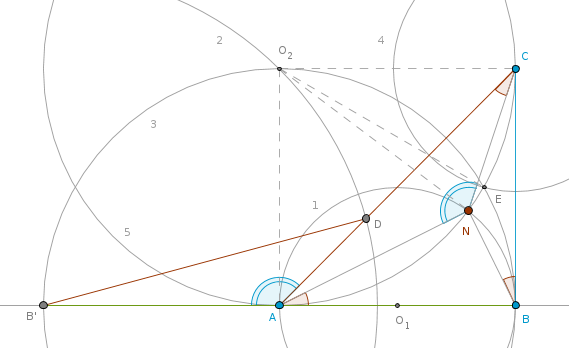
Good job, guys, you are both correct. Both solutions locate N for an arbitrary triangle. To locate the second point you simply shift the Thales circle to the other side of the triangle and for jollytall's construction reflect B over C (not A) and for jollytall's son construction you bisect the angle C (not A).
Posts read like a problem-solving classic - a solution, then simplification.
I've rendered both solutions here (skipping some intermediate steps to avoid the clutter):
jollytall:
jollytall's son:
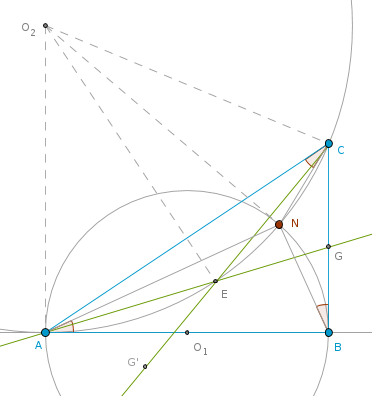
Small clarification for the readers: in the above construction you bisect the angle CAB by AG. Then you construct an angle ACG' such that ACG' = CAG (=BAG). AG intersects CG' at E ...
If you want to try to simplify the construction even more - take some time to ponder, otherwise I will post my (search for and a) solution, for completeness, which is just a bit simpler (still takes two circles) and then I will add even more simpler one - it takes just one circle but it's not mine, probably belongs to the problem's author.
The best hint I can come up with for my solution is don't work with angle bisectors, try working with the side CB and the hypotenuse AC or better yet - it's vertex C. Sorry if it's too vague. Let me know if I need to be more specific.
|
|
IP Logged |
|
|
|
jollytall
Senior Riddler
Gender:
Posts: 585
|
|
Re: Brocard Point(s).
« Reply #4 on: May 20th, 2014, 3:05am » |
Quote Modify
|
Thanks for the great drawings. Actually I am always lazy to draw on the computer (or maybe I need a good software to do so).
OFF
Also, I did not have paper with me, so we had to do it in "head"  . It made me really happy that my 14 year old could do it without even seeing the problem...
|
|
IP Logged |
|
|
|
rloginunix
Uberpuzzler
Posts: 1029
|
|
Re: Brocard Point(s).
« Reply #5 on: May 20th, 2014, 11:11am » |
Quote Modify
|
Wow! You guys are incredible. The fact that you have a fourteen-year-old who can solve these problems in his mind tells me there's hope for this planet still. Keep up the great work.
I use GeoGebra or Cinderella for technical drawings. Both are Java-based, free of charge and easy to use. I run mine on the beat up old OpenSuse laptop.
Now, simplifying a solution may be just as much fun as it is educational. The next time you can grab a piece of paper and a pencil (or the software) think "less straight lines".
Taking the last construction as a base line - AB's bisector to locate O1. That's 1 straight line. Plus 2 angle bisectors - that's 3. Plus 2 straight lines to locate O2 - that's 5 straight lines, 2 circles. (I'm not counting the supporting lines).
You can do it with 2 circles and for the right triangle with 3 straight lines or for any triangle with 4 straight lines.
I used Euclid's Book III Proposition 32 to get to this construction. It basically says that the angles between the chord and the tangent to a circle at the tangency point and the angles on its circumference are locked into a type of equality relationship.
For even more simpler way it can be done with 1 circle and for the right triangle with 3 straight lines and for any triangle with 4 straight lines.
|
|
IP Logged |
|
|
|
rloginunix
Uberpuzzler
Posts: 1029
|
|
Re: Brocard Point(s).
« Reply #6 on: May 23rd, 2014, 9:06am » |
Quote Modify
|
Those willing to exercise their wits at finding simpler constructions be forewarned - some solutions are coming up.
We notice quickly that the angle ANB must be right (as shown by jollytall). Any point on the circumference of the circle built with AB as its diameter satisfies that requirement (Thales or B3.P31). Hence one locus of points N is the arc of such a circle trapped inside the triangle.
We need the second locus, intersecting the first one, to locate N exactly. My idea was to introduce a point P such that the angle PCA equals the angle PBC. If, by some manipulation, I can make the points P and N coincide I will hopefully find the second locus:
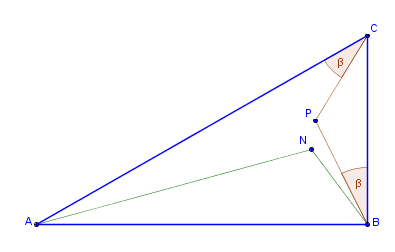
A few such points out of infinite amount possible look like so:
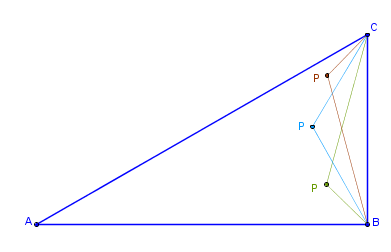
Hunch: points sit on another arc of another circle trapped inside the triangle. Not clear how to locate its center and radius. Simplify. Instead of working with an acute angle ACB ruin the triangle temporarily by unbuckling the hypotenuse AC and making the angle ACB right:
Observations. Points sit on a half circumference of a circle with BC as its diameter (located by bisecting BC) and AC as a tangent. Put the triangle back together. Imagine AC being welded to the circle CO1B at C and you pushing it down as a lever at A:
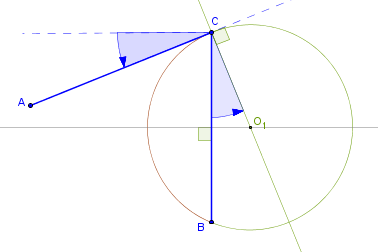
When things lock into place it becomes clear that the second circle has the hypotenuse AC as its tangent and its center is at the intersection of a perpendicular to AC at C and BC's perpendicular bisector:
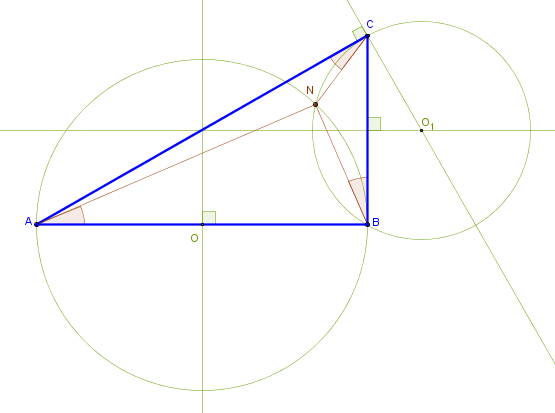
The proof that it must be so is simple with a small extra construction:
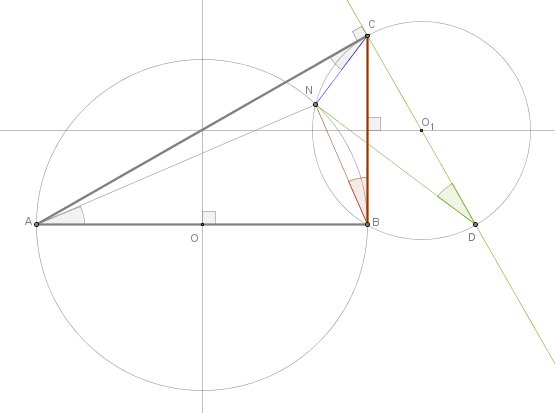
Applying B3.P32 (tangent and the alternate segments) to AC, circle CO1B and the angle NDC yields NCA = NDC. But NDC and NBC subtend the same arc NC hence, B3.P21, they are equal. Hence, NBC = NCA.
To generalize for any triangle construct the first circle as you did the second one: bisect AB, draw a perpendicular to CB at B. The intersection of two perpendiculars locates the center, O2, and O2A = O2B as its radius. 4 straight lines, 2 circles.
|
|
IP Logged |
|
|
|
rloginunix
Uberpuzzler
Posts: 1029
|
|
Re: Brocard Point(s).
« Reply #7 on: May 23rd, 2014, 9:15am » |
Quote Modify
|
Lastly, a 1-circle solution.
From as much as I can gather it belongs to Mr. Jozsef Kurschak (1864-1933) but I could be wrong as the book does not explicitly state so. It is also based on B3.P32.
Perpendicular to AB through B.
Bisect BC.
These two intersect at D.
Circle(D, DB).
Parallel to CA through B intersects the circle(D, DB) at E.
Straight line AE intersects the circle(D, DB) at N:
|
|
IP Logged |
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print