 Author
Author |
Topic: PPT (a^2, b^2, c) (Read 810 times) |
|
Christine
Full Member
  

Posts: 159
|
 |
PPT (a^2, b^2, c)
« on: Dec 23rd, 2014, 1:04pm » |
 Quote Quote  Modify Modify
|
Is it possible to find a PPT of the form (a^2, b^2, c) ?
Why or why not?
|
|
 IP Logged IP Logged |
|
|
|
dudiobugtron
Uberpuzzler
    

Posts: 735
|
 |
Re: PPT (a^2, b^2, c)
« Reply #1 on: Dec 23rd, 2014, 2:53pm » |
 Quote Quote  Modify Modify
|
You don't need the primitive condition - if it's possible to find any pythagorean triple of that form, then you can find a primitive one.
|
|
 IP Logged IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: PPT (a^2, b^2, c)
« Reply #2 on: Dec 23rd, 2014, 11:17pm » |
 Quote Quote  Modify Modify
|
From Euclid's formula we get that
a2 = m2 - n2
b2 = 2mn
c = m2 + n2
with m > n, m - n = odd and m,n coprime.
For b to be square and m,n coprime, we need
m,n = x2, 2 y2 ( and x odd) or
m,n = 2 x2, y2 ( and y odd)
So if there is such a triple, it needs to conform to either
a2 = x4 - 4 y4, b2 = 4 x2 y2, c = x4 + 4 y4 or
a2 = 4 x4 - y4, b2 = 4 x2 y2, c = 4 x4 + y4
So, can anyone find a square |4 x4 - y4| ?
|
| « Last Edit: Dec 23rd, 2014, 11:19pm by towr » |
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Christine
Full Member
  

Posts: 159
|
 |
Re: PPT (a^2, b^2, c)
« Reply #3 on: Dec 24th, 2014, 12:59am » |
 Quote Quote  Modify Modify
|
This is what I get:
4 x^4 - y^4 = z^2
(2 x^2 - y^2) (2 x^2 + y^2) = z^2
the only integer solution is x = y = z = 0
So, no PPT
|
|
 IP Logged IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: PPT (a^2, b^2, c)
« Reply #4 on: Dec 24th, 2014, 8:58am » |
 Quote Quote  Modify Modify
|
There are more solutions that don't work: y=0, z=2 x2
Since z needn't be prime, I think it's too soon to declare there are no valid solutions.
For example if we had (2x - y)(2x + y) = z^2, then x=82, y=36, z=160 would be a solution. So these types of equations can have non-trivial solutions.
|
|
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: PPT (a^2, b^2, c)
« Reply #5 on: Dec 24th, 2014, 12:08pm » |
 Quote Quote  Modify Modify
|
a2 also has to be odd
Which means that modulo 8, it's 1 (because it's not 0 or 4)
4 x4 - y4 modulo 8 is 0, 3, 4 or 7, so it can't equal a2
x4 - 4 y4 modulo 8 is 0, 1, 4 or 5, which can equal a2 modulo 8. So if there is a solution, we need to look for it here.
|
|
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
rloginunix
Uberpuzzler
    

Posts: 1029
|
 |
Re: PPT (a^2, b^2, c)
« Reply #6 on: Dec 26th, 2014, 8:08pm » |
 Quote Quote  Modify Modify
|
Guys, correct me if I am wrong but it feels like you should be able to use Fermat's own method of infinite descend here. So all credits go to the master.
It is basically a proof by contradiction - we assume that a smallest (positive) integer solution exists, massage it some, and then arrive at a contradiction that yet another even smaller integer solution exists.
I have used so many intermediate variables that I have numbered all the statements to make finding a mistake easy.
We seek, in general, integer solutions for an equation:
x4+ y4 = z2 (1)
Given the problem statement let us assume that we have found three integers "a", "b", and "c" such that:
a4+ b4 = c2 (2)
and "c" is the smallest possible solution integer and gcd(a, b, c) = 1. Rewrite the left hand side terms as:
(a2)2 + (b2)2 = c2 (3)
From towr's Reply #2 we must have:
a2 = m2 - n2 (4)
b2 = 2mn (5)
c = m2 + n2 (6)
m > n, m - n = 2 + 1, gcd(m, n) = 1 (7) + 1, gcd(m, n) = 1 (7)
This is adjusted for (3). From (6) it follows that:
m < c (8)
Let us work with (4) since all its powers are 2's and we know how deal with them if we carry the "n" term over to the left side of the equal sign:
a2 + n2 = m2 (9)
Again, from towr's Reply #2 for the above to be true we must have:
a = p2 - q2 (10)
n = 2pq (11)
m = p2 + q2 (12)
p > q, p - q = 2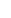 + 1, gcd(p, q) = 1 (13) + 1, gcd(p, q) = 1 (13)
Here I have switched the expressions for "a" and "n" around. From (5), since "b2" must be a perfect square, it follows that:
m = r2 (14)
n = 2s2 (15)
gcd(r, s) = 1 (16)
Now "n" is expressed twice: once in (11) and once in (15), hence:
2pq = 2s2 (17)
pq = s2 (18)
Again, since "s2" must be a perfect square:
p = u2 (19)
q = v2 (20)
Square (19) and (20) separately and then sum them:
u4 + v4 = p2 + q2 (21)
Put (12) into (21):
u4 + v4 = p2 + q2 = m (22)
Put (14) into (22):
u4 + v4 = p2 + q2 = m = r2 (23)
From where it follows that:
r 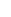 m < c (24) m < c (24)
which contradicts the assumption that "c" is the smallest integer solution. Hence, you can not have a primitive Pythagorean triple of the form {a2, b2, c}.
(may be someone can shorten the proof)
|
|
 IP Logged IP Logged |
|
|
|
rloginunix
Uberpuzzler
    

Posts: 1029
|
 |
Re: PPT (a^2, b^2, c)
« Reply #7 on: Dec 28th, 2014, 9:27pm » |
 Quote Quote  Modify Modify
|
If we change the plus sign to a minus in (1) above and shuffle the variables' names a bit:
z4 - x4 = y2 (2.1)
the question then becomes "does a primitive Pythagorean triple of the form {a2, b, c2} exist"? Looks like the answer is negative. The proof is almost the carbon copy of the one above except that at the end instead of a sum we take the difference.
In a condensed form, using towr's Reply #2 formulas:
(x2)2 + y2 = (z2)2 (2.2)
x2 = 2mn (2.3)
y = m2 - n2 (2.4)
z2 = m2 + n2 (2.5)
m < z (2.6)
(2.5):
m = p2 - q2 (2.7)
n = 2pq (2.8)
z = p2 + q2 (2.9)
(2.3):
m = r2 (2.10)
n = 2s2 (2.11)
(2.8), (2.11):
pq = s2 (2.12)
(2.12):
p = u2 (2.13)
q = v2 (2.14)
(2.14), (2.13), (2.7), (2.10):
u4 - v4 = p2 - q2 = m = r2 (2.15)
(2.15):
r 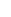 m < z (2.16) m < z (2.16)
which violates the Well Ordering Principle, "z" was assumed to be the smallest positive integer solution ...
|
|
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register