 Author
Author |
Topic: Inequality: A_(n+1)^(n+1) >= A_n^n * x_(n+1) (Read 938 times) |
|
anonymous
Guest

|
 |
Inequality: A_(n+1)^(n+1) >= A_n^n * x_(n+1)
« on: Jun 11th, 2003, 5:42am » |
 Quote Quote  Modify Modify
 Remove Remove
|
Let x1,x2,x3,... be positive real numbers. For positive integer n, denote An=(x1+x2+...+xn)/n.
Use the inequaltiy (a+b)n >= an + nan-1b to prove that
(An+1)n+1 >= (An)n . xn+1
for all positive integer n.
// title modified by William Wu on 3:47 AM 8/31/2003; please use slightly more descriptive titles, thank you
|
| « Last Edit: Aug 31st, 2003, 3:47am by william wu » |
 IP Logged IP Logged |
|
|
|
TenaliRaman
Uberpuzzler
    

I am no special. I am only passionately curious.
Gender: 
Posts: 1001
|
 |
Re: Inequality: A_(n+1)^(n+1) >= A_n^n * x_(n+1) 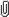 tex2gif.gif tex2gif.gif
« Reply #2 on: Sep 6th, 2003, 11:38pm » |
 Quote Quote  Modify Modify
|
Following wu's approach and a bit of modification i arrived at this,
[edit]P.S -> the image looks a bit tarnished.hopefully its readable![/edit]
|
| « Last Edit: Sep 6th, 2003, 11:42pm by TenaliRaman » |
 IP Logged IP Logged |
Self discovery comes when a man measures himself against an obstacle - Antoine de Saint Exupery
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
    

Boldly going where even angels fear to tread.
Gender: 
Posts: 4863
|
 |
Re: Inequality: A_(n+1)^(n+1) >= A_n^n * x_(n+1)
« Reply #3 on: Sep 7th, 2003, 1:15pm » |
 Quote Quote  Modify Modify
|
on Sep 6th, 2003, 11:38pm, TenaliRaman wrote:| [edit]P.S -> the image looks a bit tarnished.hopefully its readable![/edit] |
|
Unfortunately, no it is not. Can you recreate it using the new math symbolry?
|
|
 IP Logged IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Pietro K.C.
Full Member
  

 

Gender: 
Posts: 213
|
 |
Re: Inequality: A_(n+1)^(n+1) >= A_n^n * x_(n+1)
« Reply #4 on: Sep 7th, 2003, 1:52pm » |
 Quote Quote  Modify Modify
|
The first thing I tried was Wu's approach, which is the most immediate, given the hint. I got to the same place as him, and also got stuck. But then I noticed that it is IMPOSSIBLE to demonstrate the theorem in this fashion, i.e. applying the hint in just such a manner. I'll try to show why.
[Below, n/n+1 wil denote n/(n+1), which, although correct, clutters the formulas with parentheses]
We both started by noticing that
An+1 = (n/n+1) An + xn+1/(n+1)
and using the
(1) (a + b)n [ge] an + nan-1b
inequality on it in the obvious way. We both got
(2) An+1n+1 [ge] (n/n+1)n+1Ann+1 + (n/n+1)nAnn xn+1.
To use this formula in the demonstratin that
(3) An+1n+1 [ge] Ann xn+1 ,
we would have to show that the right side of (2) is greater than, or equal to, the right side of (3).
But that is just not the case. See, unless b = 0 in (1), the left side is strictly larger than the right; however, there are cases where
An+1n+1 = Ann xn+1 exactly.
For instance, if all the xi are equal to the same positive constant c, then Ai = c for all natural i. Therefore, the needed inequality is false in general, and this particular use of the hint will get us nowhere.
I was able to demonstrate the formula without (1), and it turned out to be pretty simple. Is the requirement of using (1) part of the challenge? My proof is hidden below.
Start by noticing that An+1 is the arithmetic mean of the set { An, ... , An, xn+1 }, where An appears n times. Using the well-known inequality between arithmetic and geometric means, we get
An+1 [ge] (Ann xn+1)1/(n+1), whence
An+1n+1 [ge] Ann xn+1.
|
| « Last Edit: Sep 7th, 2003, 8:54pm by Pietro K.C. » |
 IP Logged IP Logged |
"I always wondered about the meaning of life. So I looked it up in the dictionary under 'L' and there it was --- the meaning of life. It was not what I expected." (Dogbert)
|
|
|
TenaliRaman
Uberpuzzler
    

I am no special. I am only passionately curious.
Gender: 
Posts: 1001
|
 |
Re: Inequality: A_(n+1)^(n+1) >= A_n^n * x_(n+1) 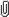 tex2gif.bmp tex2gif.bmp
« Reply #5 on: Sep 8th, 2003, 10:08am » |
 Quote Quote  Modify Modify
|
hmm lemme see,
is this any helpful in proving the inequality??(i tried some way of relating this RHS with the original RHS but haven't found anyway so far.....)
|
| « Last Edit: Sep 8th, 2003, 10:10am by TenaliRaman » |
 IP Logged IP Logged |
Self discovery comes when a man measures himself against an obstacle - Antoine de Saint Exupery
|
|
|
Aryabhatta
Uberpuzzler
    

Gender: 
Posts: 1321
|
 |
Re: Inequality: A_(n+1)^(n+1) >= A_n^n * x_(n+1)
« Reply #6 on: Jun 8th, 2004, 3:46pm » |
 Quote Quote  Modify Modify
|
on Sep 7th, 2003, 1:52pm, Pietro K.C. wrote:
I was able to demonstrate the formula without (1), and it turned out to be pretty simple. Is the requirement of using (1) part of the challenge? My proof is hidden below.
Start by noticing that An+1 is the arithmetic mean of the set { An, ... , An, xn+1 }, where An appears n times. Using the well-known inequality between arithmetic and geometric means, we get
An+1 [ge] (Ann xn+1)1/(n+1), whence
An+1n+1 [ge] Ann xn+1.
|
|
I guess the motivation for proving this inequality was to prove that AM [ge] GM, as AM [ge] GM follows immediately from it by induction on n.
We can prove the inequality An+1n+1 [ge] Ann xn+1 under the assumption that x1 [le] x2 [le] ... [le] xn [le] xn+1
If we assume that the xi's are non-decreasing, it follows that An+1 [ge] An. The case when An+1 = An is easy. So assume An+1 > An.
Let An+1/An = 1 + h. h > 0.
By applying (a+b)[supn] [ge] a[supn] + nan-1b, we get
(An+1/An)n+1 = (1+h)n+1 [ge] 1 + (n+1)h = 1 + (n+1)(An+1/An - 1) = xn+1/An which implies
An+1n+1 [ge] Ann xn+1
This proves AM [ge] GM for arbitrary positive xi's since we can arrange them in nondecreasing order and relabel them as y1 [le] y2 [le] ... [le] yn [le] yn+1. For these yi's we have just shown that AM [ge] GM. This implies AM [ge] GM for the xi's as (y1,...,yn+1) is just a permutation of (x1,...,xn+1).
Incidentally, once we have proved AM [ge] GM, we can use this to show that(using Pietro's post)
An+1n+1 [ge] Ann xn+1 for any positive xi's i.e. without the restriction that x1 [le] x2 [le] ... [le] xn [le] xn+1
|
|
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register