Author |
Topic: Mutually Rational Distances (Read 5654 times) |
|
Aryabhatta
Uberpuzzler
Gender: 
Posts: 1321
|
 |
Mutually Rational Distances
« on: Dec 16th, 2004, 11:58am » |
 Quote  Modify
|
Show that we can find an infinite set of points S on the circumference of a circle of diameter 1, such that the distance between any two points of that set is rational.
i.e given a circle C of diameter 1, Show existence of an S such that:
if P [in] S then P lies on C.
if P [in] S and Q [in] S then distance between P and Q is rational.
S is not finite.
Sorry if this problem has appeared before, but the search on this site has become really slow...
|
|
 IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
|
Re: Mutually Rational Distances
« Reply #1 on: Dec 16th, 2004, 3:40pm » |
Quote Modify
|
Are we talking about intrinsic distance (arclength), or extrinsic distance (chordlength)?
|
|
IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Aryabhatta
Uberpuzzler
Gender:
Posts: 1321
|
|
Re: Mutually Rational Distances
« Reply #2 on: Dec 16th, 2004, 4:44pm » |
Quote Modify
|
on Dec 16th, 2004, 3:40pm, Icarus wrote:| Are we talking about intrinsic distance (arclength), or extrinsic distance (chordlength)? |
|
The chord length.
If we consider the arc length, then it is not possible to have such an arrangement. (Pick any 3, add up the 3 arcs which complete the circle, we get that [pi] is rational)
|
|
IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
|
Re: Mutually Rational Distances
« Reply #3 on: Dec 16th, 2004, 7:58pm » |
Quote Modify
|
Actually, it is, but instead of being impossible, the solution is trivial: consider all points eir, for rational r, 0 [le] r < [pi]. Since the arclength between two points is measured by the shorter arc, the irrational longer arc between any two such points is immaterial.
Still, trivial is no better than impossible in this regard. My request for clarification was unnecessary with a little thought.
|
|
IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
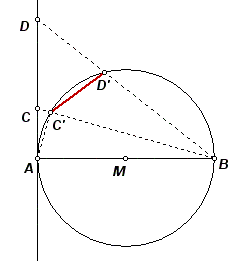
Usually, drawings are not used in Putnam section, but in this particular case one comes handy.
Take a segment AB of unit length, and construct a circle with AB as diameter. Next, draw a perpendicular line through A. Pick two points C, D on that line so that the lengths |AC|, |AD| are of the form
(n2-m2)/2nm, (1)
where n, m are positive integers. Let C’, D’ be intersections of BC, BD with the circle. Then, |C’D’| is rational.
To prove this, consider for instance points C, C’. Clearly, |BC| = (n2+m2)/2nm, hence rational. Because |BC| [cdot] |BC’| = 1 (why?), |BC’| = 2nm/(n2+m2), also rational. Then, |AC’| = (n2-m2)/(n2+m2), again rational. Analogously, |AD’|, |BD’| are rational. Now, look at the quadrilateral AC’D’B – it’s cyclic, and has 3 sides and 2 diagonals rational. According to Ptolemy’s theorem, the remaining side C’D’ should also be rational.
To complete the proof of the problem’s statement, note that infinitely many points of the form (1) may be chosen on the line.
|
| « Last Edit: Dec 17th, 2004, 12:55am by Barukh » |
IP Logged |
|
|
|
Aryabhatta
Uberpuzzler
Gender:
Posts: 1321
|
|
Re: Mutually Rational Distances
« Reply #5 on: Dec 17th, 2004, 10:41am » |
Quote Modify
|
Nicely done Barukh!
The solution I have is similar.
Consider diameter 1 circle centered at (0,0). Let P be (1/2,0) and Q be (-1/2,0) (End points of the horizontal diameter).
Consider any two pythogarean (rational) triples (x1,y1,1) and (x2,y2,1) i.e xi2 + yi2 = 1.
Picks points A1 and A2 on the 'top' semicircle of the circle such that |AiP| = xi and |AiQ| = yi. This is possible as AiPQ is a right angled triangle.
(|XY| = distance between points X and Y)
By Ptolemy's theorem, |A1A2| is rational.
Since we have infinitely many such A's we are done.
|
| « Last Edit: Dec 17th, 2004, 10:42am by Aryabhatta » |
IP Logged |
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: Mutually Rational Distances
« Reply #6 on: Dec 18th, 2004, 9:16am » |
Quote Modify
|
The following related question is much harder:
How many points can be drawn in the plane in general position (i.e. no 3 points on the same line, no 4 points on the same circle) so that their mutual distances are all integers?
|
|
IP Logged |
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print