 Author
Author |
Topic: Sets closed under closure and complementation (Read 906 times) |
|
Deedlit
Senior Riddler
   

Posts: 476
|
 |
Sets closed under closure and complementation
« on: Aug 4th, 2006, 4:24pm » |
 Quote Quote  Modify Modify
|
I don't remember whether I asked this before, but it's a problem I like a lot.
Let S be a subspace of a topological space X. Let T be the collection of spaces generated by S under topological closure and complementation.
For example, if X = R, S = [0,1], then, letting ~Y and CY be the complement and closure of Y, respectively,
we have
S = [0,1]
~S = (-inf, 0) U (1, inf)
C~S = (-inf, 0] U [1, inf)
~C~S = (0,1),
and all taking the closure or complement of any of the four sets just gets us one of the four sets. So T has 4 elements.
What cardinalities can T have, for arbitrary S and X?
|
|
 IP Logged IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
    

Boldly going where even angels fear to tread.
Gender: 
Posts: 4863
|
 |
Re: Sets closed under closure and complementation
« Reply #1 on: Aug 4th, 2006, 6:42pm » |
 Quote Quote  Modify Modify
|
A nice challenge. It is obvious that if it is finite, the cardinality of T must be even, since complementation is a bijective operation that does not carry any set to itself. Hence each element of T can be paired uniquely with its complement.
Beyond that, however, I'll have to dust off my very rusty point-set topology!
|
|
 IP Logged IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
    

Boldly going where even angels fear to tread.
Gender: 
Posts: 4863
|
 |
Re: Sets closed under closure and complementation
« Reply #2 on: Aug 6th, 2006, 7:42am » |
 Quote Quote  Modify Modify
|
I believe that the limiting factor is this:
Lemma: If A is open, then CA = C~C~CA.
Proof: Note that since ~CA 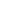 C~CA, we have ~C~CA C~CA, we have ~C~CA 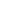 CA, and since CA is closed, C~C~CA CA, and since CA is closed, C~C~CA 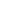 CA. CA.
Since A is open, ~A is closed and similarly contains ~CA, hence C~CA 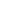 ~A. So A ~A. So A 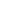 ~C~CA, and hence CA ~C~CA, and hence CA 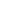 C~C~CA. C~C~CA.
So, choose an arbitrary set S. You can have the following sequence in T: S, CS, ~CS (which is open), C~CS, ~C~CS, C~C~CS, ~C~C~CS. However, by the lemma, C~C~C~CS = C~CS, so no new sets are created beyond this point. The same thing happens when you start with ~S instead of S.
Hence the cardinality of T must be within the set {2,4,6,8,10,12,14}.
I believe all are possible, but will have to work out some examples to show it.
|
|
 IP Logged IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
    

Boldly going where even angels fear to tread.
Gender: 
Posts: 4863
|
 |
Re: Sets closed under closure and complementation
« Reply #3 on: Aug 6th, 2006, 9:38am » |
 Quote Quote  Modify Modify
|
There are probably simpler examples, but here is one that gives card(T) = 12:
X = [0,3] (the entires reals will work, but this is easier symbolically).
S = ( (0,1)  Q ) Q )  (1,2) (1,2)  {3} {3}
Where Q is the rationals. Letting an exponent of Q or I mean that the set is intersected with the rationals or irrationals respectively, we find that
CS = [0,2]  {3} {3}
~CS = (2,3)
C~CS = [2,3]
~C~CS = [0,2)
C~C~CS = [0,2]
~C~C~CS = (2,3]
~S = {0}  (0,1]I (0,1]I  [2,3) [2,3)
C~S = [0,1]  [2,3] [2,3]
~C~S = (1,2)
C~C~S = [1,2]
~C~C~S = [0,1)  (2, 3] (2, 3]
|
| « Last Edit: Aug 6th, 2006, 9:42am by Icarus » |
 IP Logged IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
    

Boldly going where even angels fear to tread.
Gender: 
Posts: 4863
|
 |
Re: Sets closed under closure and complementation
« Reply #4 on: Aug 6th, 2006, 10:00am » |
 Quote Quote  Modify Modify
|
A small change gives card(T) = 14:
X = [0,4]
S = [0,1]I  (1,2) (1,2)  (2,3) (2,3)  {4} {4}
CS = [0,3]  {4} {4}
~CS = (3,4)
C~CS = [3,4]
~C~CS = [0,3)
C~C~CS = [0,3]
~C~C~CS = (3,4]
~S = [0,1]Q  {2} {2}  [3,4) [3,4)
C~S = [0,1]  {2} {2}  [3,4] [3,4]
~C~S = (1,2)  (2,3) (2,3)
C~C~S = [1,3]
~C~C~S = [0,1)  (3, 4] (3, 4]
C~C~C~S = [0,1]  [3, 4] [3, 4]
~C~C~C~S = (1,3)
Removing various elements from S (regions where both S and ~S are dense, regions where each alone is present, isolated points in each) will give the various lesser values for Card(T). Card(T) = 2 can be obtained by letting S = X.
|
| « Last Edit: Aug 6th, 2006, 10:13am by Icarus » |
 IP Logged IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Michael Dagg
Senior Riddler
   

Gender: 
Posts: 500
|
 |
Re: Sets closed under closure and complementation
« Reply #5 on: Aug 7th, 2006, 10:47am » |
 Quote Quote  Modify Modify
|
Nice!
This well-known problem is attributed to Kuratowski
and called the 14-set theorem.
|
| « Last Edit: Aug 7th, 2006, 2:00pm by Michael Dagg » |
 IP Logged IP Logged |
Regards,
Michael Dagg
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
    

Boldly going where even angels fear to tread.
Gender: 
Posts: 4863
|
 |
Re: Sets closed under closure and complementation
« Reply #6 on: Aug 7th, 2006, 8:58pm » |
 Quote Quote  Modify Modify
|
Since pointless abstraction is a cornerstone of mathematics (and I was curious which properties of closure this result depended upon):
Theorem: Let (X, <) be a partially ordered set, and let R,T be two operators on X such that
(1) T is [cant remember the term!] (T2 = I),
(2) R is idempotent (R2 = R)
(3) R is increasing, and T is decreasing (if x <= y, then Rx <= Ry and Tx >= Ty),
(4) For all x, Rx >= x.
Let <x> be the span of x under R & T (i.e., the smallest set containing x and closed under the operators). Then card(<x>) <= 14 for all x.
(The proof is identical, just replacing C and ~ by R & T, and interpreting "x is closed" to mean that there exists y such that x = Ry, and "x is open" to mean x = TRy for some y.)
|
|
 IP Logged IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Michael Dagg
Senior Riddler
   

Gender: 
Posts: 500
|
 |
Re: Sets closed under closure and complementation
« Reply #7 on: Aug 8th, 2006, 9:23am » |
 Quote Quote  Modify Modify
|
>Since pointless abstraction is a cornerstone of mathematics...
Some may argue that is a little harsh but I have to agree will you.
But in fact if memory serves, Kuratowski was interested in setting
up his analysis of topology in just this way: rather than defining things
in terms of a family of sets called the "open sets", or in terms of a family
of sets called the "closed sets", he defined a topological space to be a
set X together with a "closure operator", i.e. your map R : 2^X --> 2^X
subject to axioms like yours. I don't think he went as far as to free T
from its intended definition of being complementation (it's an "operator
of order 2", by the way -- T^2 = I ), nor do I think he was interested in
looking at more general posets than the power set 2^X of a set X.
But IIRC he believed the closure operator better defined what a topology
(and especially continuity) was really all about: we want to know what we
can get by taking limits of (say) nice Fourier series, which means we
want to know the closure of "nice" families of functions; and the definition
of continuity in terms of inverse images of open sets is not nearly as
intuitive as saying that limits should map to limits which, again, is really
a statement about closures (well, sort of). I don't think Kuratowski's plan
caught on, though it might have had better success in areas where people
are looking at fractals and things like that.
But who knows; maybe you've got the right idea by generalizing to the
level of posets with two intertwined operators. Prove that some well-known
results in topology are true more generally, and have an easier proof in
the broader context, and you'll likey make it better for the rest of us.
|
| « Last Edit: Aug 8th, 2006, 12:48pm by Michael Dagg » |
 IP Logged IP Logged |
Regards,
Michael Dagg
|
|
|
Michael Dagg
Senior Riddler
   

Gender: 
Posts: 500
|
 |
Re: Sets closed under closure and complementation
« Reply #8 on: Aug 8th, 2006, 11:11am » |
 Quote Quote  Modify Modify
|
My previous remarks suggested that it might be a nice generalization of
"topological space" to move from having two operators on Y = 2^X, one of them
specifically being complementation, to having two operators on a more
general poset, one of them simply being of order 2 and order-reversing.
A general plan for getting theorems out of this setting would be
to try to prove theorems which you know to be true for topological
spaces. The main difficulty of course is that if all you have is a poset Y
(and the two operators) then you can't talk about "points (in X)" or
sequences of them or sets of them as such. On the other hand,
the following fact is true: you can more or less recover a topological
space from the family of continuous functions defined on it; at least, I know
it's true that C^0 ( R^n , R ) can be given the structure of a ring
in such a way that the rings differ when n is varied. So as a step in
the right direction you might want to consider the general case of a
poset-with-two-operators and immediately start to consider the ring of
"countinuous" maps on it (where obviously you will define this in some
way that is consistent with what would be observed if Y = 2^X).
As always one never knows in advance how well the generalizations will
go -- it could be that this is going to be very technical and dreary
when Y isn't 2^X and T isn't complementation; but it could turn
out to have a very clean description with some elegant theorems.
|
| « Last Edit: Aug 8th, 2006, 11:12am by Michael Dagg » |
 IP Logged IP Logged |
Regards,
Michael Dagg
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
    

Boldly going where even angels fear to tread.
Gender: 
Posts: 4863
|
 |
Re: Sets closed under closure and complementation
« Reply #9 on: Aug 8th, 2006, 3:41pm » |
 Quote Quote  Modify Modify
|
Thanks for the reminder. I was thinking that there was a specific term, like idempotent and nilpotent, to describe an element whose square was the identity. But I guess the reason I couldn't think of it was because it doesn't exist (or is not widespread).
Quote:>Since pointless abstraction is a cornerstone of mathematics...
Some may argue that is a little harsh but I have to agree will you. |
|
Of course, my comment was strictly tongue-in-cheek. I didn't have any real reason for abstracting this particular problem, other than a curiousity, as I said, as to what properties of C were that caused this to work. Actually, though, I consider abstraction to be the most powerful tool in the mathematician's toolbox. I cannot recall all the times I have fought battles with a problem only to discover a year or too later that the thing was nearly trivial when approached from the right direction. The cause of my suffering was not intractability of the problem itself, but a failure on my part to recognize what was essential. Abstraction removes the unessential parts.
Curiously, I did think of another trio of poset and operators satisfying the conditions: multiplication by -1 and 1 in R. The application gives us the amazing result that by starting with a real number and multiplying repeatedly by 1 and -1, we can reach at most 13 other real numbers!  (I think it might even possible to tighten this bound!) (I think it might even possible to tighten this bound!)
I have not heard of Kuratowski's approach to topology before. It doesn't really sound more natural to me than the more traditional version (which can be stated to sound more natural than you made it). But it does sound interesting. Thanks for bringing it up.
Before you could apply more topology style proofs to my poset-with-two-operators scenario, though, you would have to have something to take the place of the union and intersection operators, so you would need a poset-with-three-operators, and a requirement that R distribute over infinite intersections and finite unions. By the time you have this, I think you are effectively back to sets, so you haven't really gained anything.
|
| « Last Edit: Aug 8th, 2006, 7:19pm by Icarus » |
 IP Logged IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Michael Dagg
Senior Riddler
   

Gender: 
Posts: 500
|
 |
Re: Sets closed under closure and complementation
« Reply #10 on: Aug 9th, 2006, 10:28am » |
 Quote Quote  Modify Modify
|
But you DO have unions and intersections! What we call A union B in
2^X is actually just the smallest element in this poset which lies above
both A and B. Of course for this to make sense we have to know that
for every A and B in the poset
(i) there is at least one C with C > A and C > B . (This can be
accomplished by assuming the poset has a maximal element, which
seems pretty unobtrusive -- we are modelling 2^X after all, and
it has a maximal element (= X).
(ii) for every A and B if we have two other elements C,D with
C>A C>B D>A D>B then there is an E with C,D > E > A,B .
That's a lot more restrictive, but it describes some well-known
type of poset. (I think the phrase is "distributive lattice".)
It's certainly more general than being 2^X for some X ; for example
you could look at the set of all divisors of an integer
N (ordered by divisibility), or the set of all ideals in a ring.
(iii) Similar conditions for intersections.
It might be interesting to look at some of these other kinds of
lattices and see if you can make examples of pairs of operators
where the Kuratowski bound is actually achieved. That might make
for a pretty article for the Monthly or something like that!
I tried to think about what the right morphisms would be in this
new category. How do you describe what makes a map f : X -> Y
continuous, if all you have is 2^X and 2^Y ? I'm not really sure.
From f you get both the forward maps f : 2^X --> 2^Y and the
inverse-image function f-inv : 2^Y --> 2^X . Am I right in thinking
that each one determines the other? e.g. if I know the map f-inv
then for an element A of 2^X we have
f(A) = intersection of all U in 2^Y with f-inv(U) > A.
Of course continuity is defined by the condition that
U = R'(U) ==> f-inv(U) = R( f-inv(U) ),
but that seems to be the same as saying f-inv commutes with the
closure operators. So you could define the morphisms in this
category to be
Mor( X, Y ) = { F : Y -> X | F preserves order, F commutes with R }.
That would be sort of disorienting: morphisms from X to Y are
actually functions from Y to X ! But it's actually OK.
I have to actually think this through a little more.
+++
(Dave Lutzer (I think) did some work similar to this but I can't find it).
Edit: Dave Lutzer did not do any work like this.
|
| « Last Edit: Aug 9th, 2006, 11:36am by Michael Dagg » |
 IP Logged IP Logged |
Regards,
Michael Dagg
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: Sets closed under closure and complementation
« Reply #11 on: Aug 11th, 2006, 12:20am » |
 Quote Quote  Modify Modify
|
on Aug 8th, 2006, 9:23am, Michael_Dagg wrote:| But in fact if memory serves, Kuratowski was interested in setting up his analysis of topology in just this way: rather than defining things in terms of a family of sets called the "open sets", or in terms of a family of sets called the "closed sets", he defined a topological space to be a set X together with a "closure operator", i.e. your map R : 2^X --> 2^X subject to axioms like yours. |
|
That would explain the Kuratowki closure axioms.
Quote:| the definition of continuity in terms of inverse images of open sets is not nearly as intuitive as saying that limits should map to limits |
|
It's also different, if by limits you mean limits of sequences, and the space can be non-metrizable. For example, define
f : omega1+1 -> {0,1} by f(x)=0 if x<omega1, and f(omega1)=1.
Then f is not continuous, even though xn->x implies f(xn)->f(x). Also, omega1 is sequentially compact but not compact.
Things are nicer with nets though: A net in a topological space X is a function from a directed set J (poset where finite subsets have upper bounds) to X; a subnet is essentially the restriction of a net to a cofinal subset of J. A net (xalpha) converges to a point x if for any neighborhood U of x, there's an alpha such that xbeta is in U for all beta>alpha. Then f : X->Y is continuous iff whenever (xalpha)->x, (f(xalpha))->f(x), and X is compact iff every net in X has a convergent subnet.
A topology is more than just limits (for example, a.e. convergence of measurable functions can't be topologized) . . . but less than a metric. Unless of course, you only care about metrizable spaces.
on Aug 8th, 2006, 11:11am, Michael_Dagg wrote:| The main difficulty of course is that if all you have is a poset Y (and the two operators) then you can't talk about "points (in X)" or sequences of them or sets of them as such. On the other hand, the following fact is true: you can more or less recover a topological space from the family of continuous functions defined on it; at least, I know it's true that C^0 ( R^n , R ) can be given the structure of a ring in such a way that the rings differ when n is varied. |
|
Ah, a neat result with easily forgettable technical conditions: just the sort of thing professors like to mention in class (but never prove, because it's "a standard result"), and the students either take it for granted, since all their other professors have said it (or something like it) before, or just don't get around to proving it before forgetting about it until the next time someone mentions it, and never taking that one course (or reading that one book) that actually contains an exact statement and proof.
It's certainly true if X is compact Hausdorff. Let B(X) be the set of maximal ideals of Cb(X,R) (bounded continuous fns); it gets the subspace topology from Spec(Cb(X,R)). If X is completely regular (so we have Urysohn functions), then sending x to {f : f(x)=0} gives an embedding of X into B(X), and in fact, B(X) is the Stone-Cech compactification of X. (If X is also compact, this gives a homeomorphism of X with B(X).)
So Cb(X,R) determines B(X), and conversely (the universal property of Stone-Cech compactification is that Cb(X,R) = C(B(X),R)). I'm sure C(X,R) gives more information, but I don't know how much, or when. For example, X=omega1 is pseudocompact, so C(X,R)=Cb(X,R)=C(B(X),R), and so X is "less" recoverable (B(X)=omega1+1), even though X is normal.
on Aug 8th, 2006, 3:41pm, Icarus wrote:| Thanks for the reminder. I was thinking that there was a specific term, like idempotent and nilpotent, to describe an element whose square was the identity. But I guess the reason I couldn't think of it was because it doesn't exist (or is not widespread). |
|
I prefer "involution" over "operator of order less than or equal to 2" (to be technically correct).
<message continued>
|
|
 IP Logged IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: Sets closed under closure and complementation
« Reply #12 on: Aug 11th, 2006, 12:21am » |
 Quote Quote  Modify Modify
|
on Aug 9th, 2006, 10:28am, Michael_Dagg wrote:But you DO have unions and intersections! What we call A union B in
2^X is actually just the smallest element in this poset which lies above
both A and B. |
|
This is called the join (sup, \wedge) if it exists; if (finite) joins always exist you have a "join/upper semilattice" (e.g., the poset of Turing degrees). If you also have meets (inf, \cap), then it's a lattice. If you have arbitrary joins and meets, it's a "complete lattice". (Turing degrees has neither meets nor countable joins.)
I'll use 0/1 for the minimal/maximal element (if it exists), + for join, and * for meet (although this conflicts with ring operations when you have a Boolean ring/lattice).
A lattice is "(uniquely) complemented" if for all x, there's a (unique) y such that x*y = 0 and x+y = 1; it is relatively complemented if every interval is itself complemented (as a sublattice). "Atoms" are elements that "cover" 0 (no element between them); a lattice is "atomic" if every element is a join of atoms ("coatomic" if every element is a meet of coatoms).
2^X has all these properties (it's also modular, geometric, and stuff). Which properties you want to keep depends on what you're trying to accomplish, though.
Quote:| (ii) for every A and B if we have two other elements C,D with C>A C>B D>A D>B then there is an E with C,D > E > A,B . That's a lot more restrictive, but it describes some well-known type of poset. (I think the phrase is "distributive lattice".) |
|
Any lattice has this property, but there are others (e.g., N with two incomparable infinities). A distributive lattice is one where
x + (y*z) = (x+y)*(x+z), or equivalently,
x * (y+z) = (x*y) + (x*z).
(A finite distributive lattice is a power set iff it's complemented iff it's atomic iff some other stuff.)
Quote:
Of course continuity is defined by the condition that
U = R'(U) ==> f-inv(U) = R( f-inv(U) ),
but that seems to be the same as saying f-inv commutes with the
closure operators. |
|
It's not quite equivalent. For example, inclusion f : [0,1] -> [0,2] is continuous, but f-inv doesn't commute with closure on (1,2). So maybe
Mor( X, Y ) = { F : Y -> X | F a {0,1}-lattice homomorphism with FR=RFR }
would be better. Whether F need commute with infinite meets and joins is another story. For example, let X be an infinite set, and define F : P(X) -> P(1) by F(A)=1 iff A is in some fixed ultrafilter on X, and F(A)=0 otherwise. Then F preserves finite meets and joins, but only represents an actual function from 1->X if the ultrafilter is principal.
However, if F : P(Y) -> P(X) commutes with arbitrary meets and joins, and F(0)=0, F(1)=1, then F does represent a well-defined function f : X->Y.
Irrelevent, but related side note: Suppose (P,<) is a pre-poset: < is reflexive, transitive, but not necessarily antisymmetric. (If we identify equivalent points (x<y & y<x), we obtain a poset: e.g., (P(N), Turing reducibility) -> Turing degrees.) Define a subset I of P to be open if I is an "order ideal": y \in I and x<y imply x \in I. This gives a bijection between finite pre-posets and finite topologies, and restricts to a bijection between finite posets and finite T0-spaces.
But anyway, this has gotten a bit silly, since I think Icarus's original point was that the problem at hand had little to do with topology: any sort of closure operator will work: R(X) = "the smallest foo containing X". Instead of "closed set", how about "subgroup", "submodule" (including "ideal" and "vector subspace")? Or the closure in an arbitrary matroid?
Here's one from model theory: Let A be an L-structure for some first-order language L. If X is a subset of A, and a is an element, we say a is algebraic over X in A (a \in aclA(X)) if there's some formula phi(x,B) of L, with (a finite set of) parameters B from X, and some n, such that phi(a,B) and \exists<n x phi(x,B) is true in A. While this is obviously based on the case of A = field, the matroidal "exchange lemma" fails in general: it is possible to have a algebraic over b, but b not algebraic over a, even when a is non-algebraic. (However, it does hold if a,b belong to some X-definable minimal set.)
|
|
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register