Author |
Topic: Pigeonholing intervals (Read 611 times) |
|
ecoist
Senior Riddler
Gender: 
Posts: 405
|
 |
Pigeonholing intervals
« on: Feb 19th, 2007, 4:36pm » |
 Quote  Modify
|
Show that, given any mn+1 real number intervals of any sort (open, closed, half-open, empty, or nonempty), where m and n are positive integers, some m+1 of them are pairwise disjoint or some n+1 of them have a nonempty intersection.
|
|
 IP Logged |
|
|
|
kiochi
Newbie
Posts: 42
|
|
Re: Pigeonholing intervals
« Reply #1 on: Feb 22nd, 2007, 10:27am » |
Quote Modify
|
isn't this just a special case of ramsey's theorem?
|
|
IP Logged |
|
|
|
ecoist
Senior Riddler
Gender:
Posts: 405
|
|
Re: Pigeonholing intervals
« Reply #2 on: Feb 22nd, 2007, 11:29am » |
Quote Modify
|
Well, a very special, and well-known, case of Ramsey's Theorem says that, in any group of 6 people, 3 are mutual friends or 3 are mutual strangers. This conclusion is false for a group of 5 people. Taking m=n=2, the posed problem says, given any 5 intervals, either 3 have a nonempty intersection or 3 are pairwise disjoint, which is true.
|
|
IP Logged |
|
|
|
TenaliRaman
Uberpuzzler
I am no special. I am only passionately curious.
Gender:
Posts: 1001
|
|
Re: Pigeonholing intervals
« Reply #3 on: Feb 22nd, 2007, 10:58pm » |
Quote Modify
|
I have been trying to prove this along the lines of,
http://www.cut-the-knot.org/pigeonhole/seq.shtml
Bleh and i am not getting anywhere.
-- AI
|
|
IP Logged |
Self discovery comes when a man measures himself against an obstacle - Antoine de Saint Exupery
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
|
Re: Pigeonholing intervals
« Reply #4 on: Feb 23rd, 2007, 3:43am » |
Quote Modify
|
The first thing I thought of is that given mn+1 real numbers, there's either an increasing subsequence of length m+1, or a decreasing subsequence of length n+1. I couldn't get that apply, but then I remembered that it can be proved by Dilworth's theorem:
| hidden: | Let P be a poset. Then either P contains an antichain of size m+1, or P is a union of at most m chains.
For intervals I,J, write I < J if I,J are disjoint and I is to the left of J. This is clearly a partial order on our mn+1 intervals. If P contains an antichain of size m+1, then we have m+1 intervals, any two of which intersect. Otherwise, P is a union of at most m chains, and one of these chains must have size at least n+1 by Pigeonhole. This gives n+1 intervals, no two of which intersect. |
This can be viewed as providing an improved Ramsey bound R(m+1,n+1) = mn+1 in the case of comparability graphs. (For the lower bound, take m copies of a complete graph on n vertices.)
It remains to show that if any two intervals intersect, then they have a common intersection. If they are all closed, this is clear since
 [ai, bi] = [ max ai, min bi ],
and pairwise intersections show that no ai > bj. And if some interval I is not closed, and intersects J1, ..., Jm, then for each i, we can find a closed interval (a point, even) Ii' 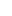 I which still intersects Ji, and replace I with convexhull( Ii') 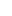I. And if these new intervals have a common intersection, certainly the old ones do.
|
|
IP Logged |
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print