 Author
Author |
Topic: Thin sets for integer functions (Read 1090 times) |
|
Pietro K.C.
Full Member
  

 

Gender: 
Posts: 213
|
 |
Thin sets for integer functions
« on: Oct 16th, 2007, 11:16pm » |
 Quote Quote  Modify Modify
|
Let N denote the natural numbers, and let
f : NČ ---> N
be any function. Prove that there is an infinite set A, contained in N, such that f(AČ) is not all of N.
Can you generalize to f : N^k ---> N? (For k=1 it's trivial.)
|
|
 IP Logged IP Logged |
"I always wondered about the meaning of life. So I looked it up in the dictionary under 'L' and there it was --- the meaning of life. It was not what I expected." (Dogbert)
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: Thin sets for integer functions
« Reply #1 on: Jan 8th, 2008, 6:51am » |
 Quote Quote  Modify Modify
|
Well now this was tricky. I started thinking about whether it was true with only finitely many colors. For example, if we color N2 using 3 colors, for {x<y}, {x=y}, and {x>y}, then clearly any infinite set A2 must use all three colors. But what about 4? Will a finite number of colors suffice? Put like this, it seemed a bit like Ramsey theory:
Infinite Ramsey theorem (IRT): Let X be some countably infinite set and colour the elements of X(n) (the subsets of X of size n) in c [finite!] different colours. Then there exists some infinite subset M of X such that the size n subsets of M all have the same colour.
Now we can use this to prove the following: if f:N2  {1,2,3,4}, then there is an infinite subset A {1,2,3,4}, then there is an infinite subset A 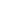 N such that f(A2) misses a value (and as we saw above, this is optimal). N such that f(A2) misses a value (and as we saw above, this is optimal).
For a<b, define fi : N(2)  {1,2,3,4} by f1({a,b})=f(a,b), f2({a,b})=f(b,a), and f3({a,b})=f(a,a). {1,2,3,4} by f1({a,b})=f(a,b), f2({a,b})=f(b,a), and f3({a,b})=f(a,a).
By IRT, we can pick an infinite set M1 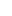 N such that f1(M1(2)) = {x} is a single value. Now, restricting f2 to M1(2), we again use IRT to pick an infinite subset M2 N such that f1(M1(2)) = {x} is a single value. Now, restricting f2 to M1(2), we again use IRT to pick an infinite subset M2 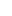 M1 such that f2(M2(2)) = {y} for some y, and then finally A M1 such that f2(M2(2)) = {y} for some y, and then finally A 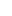 M2 with f3(A(2)) = {z}. M2 with f3(A(2)) = {z}.
Now if (a,b)  A2, either a < b, a > b, or a = b. In the first case, f(a,b) = f1({a,b}) = x; in the second, f(a,b) = f2({a,b}) = y. And in the third case we can pick b' A2, either a < b, a > b, or a = b. In the first case, f(a,b) = f1({a,b}) = x; in the second, f(a,b) = f2({a,b}) = y. And in the third case we can pick b'  A with b' > a, so that f(a,a) = f3({a,b'}) = z. So f(A2) = {x,y,z}. A with b' > a, so that f(a,a) = f3({a,b'}) = z. So f(A2) = {x,y,z}.
For arbitrary k, we can show that if f : Nk  {1,2,...,R+1}, then we can pick A such that f(Ak) misses a value, where R is the number of ways to rank k things (allowing ties). That is, we define R functions hi : N(k) {1,2,...,R+1}, then we can pick A such that f(Ak) misses a value, where R is the number of ways to rank k things (allowing ties). That is, we define R functions hi : N(k)  Nk, one using each order type, so that for any element (x1,...,xk) Nk, one using each order type, so that for any element (x1,...,xk)  Nk, we have that for some i, hi({x1,...,xk} = (x1,...,xk), roughly speaking. The complication is that if {x1,...,xk} contains fewer than k elements, we can pad the set with sufficiently large numbers. Then take fi = f hi and argue as before. Nk, we have that for some i, hi({x1,...,xk} = (x1,...,xk), roughly speaking. The complication is that if {x1,...,xk} contains fewer than k elements, we can pad the set with sufficiently large numbers. Then take fi = f hi and argue as before.
For example, with k=3, and x<y<z, we might have
h1({x,y,z}) = (x,y,z),
h2({x,y,z}) = (x,z,y),
...
h6({x,y,z}) = (z,y,x),
easy enough. Then we have to consider rankings where two are the same, say a<(b=c). This leads to
h7({x,y,z}) = (x,y,y),
so that (a,b,c) = h7({a,b,large}). Or if b < (a=c), we do
h8({x,y,z}) = (y,x,y),
so that (a,b,c) = h8({b,a,large}).
Finally
h13({x,y,z}) = (x,x,x).
In general: if T is the order type where
a1,...,ak take on r distinct values, say v1 < ... < vr, we would set the corresponding
hT({x1<x2<...<xk}) = (xj1,...,xjk),
where ji  {1,...,r} is defined by ai = vji. Clearly the definition of hT only depends on the order type T. {1,...,r} is defined by ai = vji. Clearly the definition of hT only depends on the order type T.
Now by construction, if the k-tuple (a1,...,ak) has order type T, then for L1,...,Lk-r large enough (bigger than vr), if we sort the set
S={a1,...,ak,L1,...,Lk-r} = {v1 < v2 < ... < vr < L1 < ... < Lk-r},
we get by definition
hT(S) = (vj1,...,vjk) = (a1,...,ak).
[I don't know if that actually makes it any clearer, but I needed to write it out to convince myself!]
Now of course if f : Nk  U, where U is any set with more than R elements, then we can pick a surjection s : U U, where U is any set with more than R elements, then we can pick a surjection s : U  {1,...,R+1}, and find that sf misses a value, so f did as well. {1,...,R+1}, and find that sf misses a value, so f did as well.
|
| « Last Edit: Jan 8th, 2008, 7:08am by Eigenray » |
 IP Logged IP Logged |
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 7526
|
 |
Re: Thin sets for integer functions
« Reply #2 on: Jan 8th, 2008, 7:03am » |
 Quote Quote  Modify Modify
|
on Oct 16th, 2007, 11:16pm, Pietro K.C. wrote:| Prove that there is an infinite set A, contained in N, such that f(AČ) is not all of N. |
|
Is f(AČ) = { f(a,b) | a, b in A } ?
|
|
 IP Logged IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: Thin sets for integer functions
« Reply #3 on: Jan 8th, 2008, 7:13am » |
 Quote Quote  Modify Modify
|
on Jan 8th, 2008, 7:03am, Grimbal wrote:
Is f(AČ) = { f(a,b) | a, b in A } ? |
|
Yes, as a corollary of A2 = {(a,b) | a,b in A}, and f(S) = { f(x) | x in S }.
|
|
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register