Author |
Topic: algebra (Read 1141 times) |
|
judy
Newbie
Posts: 4
|
Hey,
I'm new on this forum and I have two questions. Can you please help me?
1) M_k(F) is isomorphic to subring of M_e(F) if and only if e/k ( kle) F is a field.
2)Describe the degree 2 irreducible representation of D_4= <a,b: a^2=b^4=1, a^-1ba=b^-1>
|
| « Last Edit: Mar 24th, 2008, 10:54pm by judy » |
 IP Logged |
|
|
|
Obob
Senior Riddler
Gender: 
Posts: 489
|
 |
Re: algebra
« Reply #1 on: Mar 24th, 2008, 10:04pm » |
 Quote  Modify
|
(1) I don't know what you mean here. I take it that by Mk(F) you mean the ring of k x k matrices over the field F. And I think you are wanting to show that Mk(F) is isomorphic to a subring of Me(F) if and only if k <= e. It is important to know what is meant by "isomorphism." In particular, do isomorphisms have to preserve the identity element? And does a subring with an identity element have to have the same identity element as the larger ring? Does the isomorphism have to be F-linear?
Without at least the assumption that the isomorphism is F-linear, this problem is quite difficult (and I'm not positive it is even true, since funny things can happen like having a subfield of a field be isomorphic to the whole field). If you do assume it is F-linear, the problem becomes trivial by dimension counting.
(2) D4 is the group of symmetries of a square. Put a square in the real plane, centered around the origin (in fact, we should be able to put the square anywhere in the plane so long as none of its vertices is the origin). A symmetry of the square uniquely determines an invertible linear map of the plane. Send the symmetry to this linear map.
|
|
IP Logged |
|
|
|
judy
Newbie
Posts: 4
|
|
Re: algebra
« Reply #2 on: Mar 24th, 2008, 10:47pm » |
Quote Modify
|
ohh yes I have to write my question again. Sorry I didnt know how to use this symbols. I think it's ok now
Mk(F) is isomorphic to subring of Me(F) if and only if k l e (e divide k) F is a field.
here Mk(F) means k-by-k full
matrix algebra over F
|
| « Last Edit: Mar 24th, 2008, 10:53pm by judy » |
IP Logged |
|
|
|
Obob
Senior Riddler
Gender:
Posts: 489
|
|
Re: algebra
« Reply #3 on: Mar 25th, 2008, 12:01am » |
Quote Modify
|
Can you state what the implied definition of isomorphism is? I imagine it is "isomorphism of k-algebras with unit."
|
|
IP Logged |
|
|
|
judy
Newbie
Posts: 4
|
|
Re: algebra
« Reply #4 on: Mar 25th, 2008, 6:25am » |
Quote Modify
|
I think it's about Wedderburn-Artin theory and I have to check it under endomorphism.
|
|
IP Logged |
|
|
|
Obob
Senior Riddler
Gender:
Posts: 489
|
|
Re: algebra
« Reply #5 on: Mar 25th, 2008, 11:27am » |
Quote Modify
|
That doesn't answer my question. And what do you mean by "check it under endomorphism"? Until you have figured out what the correct definition of morphism is, the problem isn't really tractable.
|
|
IP Logged |
|
|
|
judy
Newbie
Posts: 4
|
|
Re: algebra
« Reply #6 on: Mar 26th, 2008, 5:29am » |
Quote Modify
|
I can't understand what you mean. I think here I dont need unit. I have to find an endomorphism on F and I need a maximal ideal. Don't need F is linear.
|
|
IP Logged |
|
|
|
Obob
Senior Riddler
Gender:
Posts: 489
|
|
Re: algebra
« Reply #7 on: Mar 26th, 2008, 9:25am » |
Quote Modify
|
What I mean is this: an isomorphism of Mk(F) with a subring of Me(F) is some kind of injective map f from Mk(F) to Me(F). For it to be called an isomorphism it has to satisfy some properties besides just being a function. For starters,
(1) f has to preserve addition. f(M+N)=f(M)+f(N) for all M, N in Mk(F).
(2) f has to preserve multiplication. f(MN)=f(M)f(N) for all M, N in Mk(F).
Now the question is what other axioms we require f to satisfy. In the context of Wedderburn theory, it is almost certainly the case that f must be F-linear:
(3) f is F-linear: for all t in F and M in Mk(F), we have f(tM)=tf(M).
Given the result you are trying to prove, f also has to preserve the identity matrix (or unit):
(4) f preserves the identity matrix: f(Ik)=Ie.
Without the hypothesis that f preserves the identity matrix, it is true that Mk(F) is isomorphic to a subring of Me(F) if and only if k <= e, which is not the result we are trying to prove. If we do assume f preserves the identity matrix, then it is at least easy to show that if k divides e then Mk(F) is isomorphic to a subring of Me(F): we can take a k x k matrix and put e/k copies of it along the diagonal of an e x e matrix; then since block diagonal matrices multiply block by block, this map is an isomorphism.
Endomorphisms of the field F play no role in Wedderburn theory, since one requires maps to be F-linear so that the endomorphisms of F are just given by multiplication with elements of F. I can't see how maximal ideals possibly play into this problem.
|
| « Last Edit: Mar 26th, 2008, 9:52am by Obob » |
IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
|
Re: algebra
« Reply #8 on: Mar 28th, 2008, 9:11pm » |
Quote Modify
|
My non-commutative algebra is a bit rusty I'm afraid, but I can at least prove it in this case:
Suppose there is an irreducible (over F) polynomial f(x) in F[x] of degree k. Take A  Mk(F) to be the companion matrix of f, so that A has minimal polynomial f(x). Then the image  (A) in Me(F) will still have minimal polynomial f(x). Putting (A) into rational canonical form, we see that the characteristic polynomial of (A) must be a power of f(x), proving k | e.
This argument works if F for any finite field 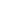 q, any global field (e.g.,  ), and any non-Archimedean local field (e.g. p). (In the latter two cases, F is the field of fractions of a domain with a non-zero prime ideal, so we can use Eisenstein's criterion to show it has irreducible polynomials of any degree.)
But it does not work for, say, algebraically closed fields like 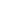 , since by definition there are no irreducible polynomials of degree > 1. Maybe we can show that restricts to a map from Mk(F')  Me(F'), where F' is the prime subfield of F? Maybe a different approach altogether is called for. But I think the characteristic polynomial of (A) should be a power of that of A (they both have the same irreducible factors, but a priori the exponents might be different).
|
| « Last Edit: Mar 28th, 2008, 9:32pm by Eigenray » |
IP Logged |
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print