Author |
Topic: Dice sum divisibility (Read 2989 times) |
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender: 
Posts: 1948
|
 |
Dice sum divisibility
« on: Aug 7th, 2008, 9:41am » |
 Quote  Modify
|
Let Sn denote the sum of n standard dice. In increasing order of difficulty:
0) If m|6, show that for all n, Sn is uniformly distributed mod m.
1) Find all m,n such that Sn is uniformly distributed mod m.
2) For each m  12, find all n such that the probability that m divides Sn is 1/m.
3) Show that for any m > 12, there are at most finitely many n for which P( m | Sn ) = 1/m.
4) Are there any pairs m,n, m > 12, for which P( m | Sn ) = 1/m?
|
| « Last Edit: Aug 30th, 2008, 12:12pm by Eigenray » |
 IP Logged |
|
|
|
l4z3r
Newbie
Posts: 10
|
|
Re: Dice sum divisibility
« Reply #1 on: Aug 30th, 2008, 5:44am » |
Quote Modify
|
on Aug 7th, 2008, 9:41am, Eigenray wrote:
Sn is uniformly distributed mod m.
|
|
i dont get this. uniformly distributed?
|
|
IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: Dice sum divisibility
« Reply #2 on: Aug 30th, 2008, 11:37am » |
Quote Modify
|
on Aug 30th, 2008, 5:44am, l4z3r wrote:| i dont get this. uniformly distributed? |
|
It means any residue modulo m is equally probable.
So take, for example: n=2 m=6
We can get sums
2 (x1), 3 (x2), 4 (x3), 5 (x4), 6 (x5), 7 (x6), 8 (x5), 9 (x4), 10 (x3), 11 (x2), 12 (x1)
modulo 6, we get
2 = 2 (mod 6) x1
3 = 3 (mod 6) x2
4 = 4 (mod 6) x3
5 = 5 (mod 6) x4
6 = 0 (mod 6) x5
7 = 1 (mod 6) x6
8 = 2 (mod 6) x5
9 = 3 (mod 6) x4
10 = 4 (mod 6) x3
11 = 5 (mod 6) x2
12 = 0 (mod 6) x1
So we have 6 out of 36 of each of 0..5 (mod 6), they are all equally probable residues.
|
|
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
|
Re: Dice sum divisibility
« Reply #3 on: Aug 30th, 2008, 12:14pm » |
Quote Modify
|
How about starting with something easier then:
0) If m|6, show that for all n, Sn is uniformly distributed mod m.
That is, S1 is uniformly distributed mod m if and only if (for all n, Sn is uniformly distributed mod m).
Hint for the rest: generating functions and roots of unity.
|
|
IP Logged |
|
|
|
Michael Dagg
Senior Riddler
Gender:
Posts: 500
|
|
Re: Dice sum divisibility
« Reply #4 on: Aug 31st, 2008, 5:50pm » |
Quote Modify
|
Nice problem set.
In Towr's example, the probability mass function of the sum
is a triangle, so the sum of the slopes at the two sides is
a constant. This does not seem to be true for n>2 . (Generalizing,
it seems to work also with n=2 and any m , if you use m-sided
rather than 6-sided dice.)
|
|
IP Logged |
Regards,
Michael Dagg
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: Dice sum divisibility
« Reply #5 on: Sep 1st, 2008, 12:34am » |
Quote Modify
|
Mod 6, any extra die just adds a random "shift", uniformly. So it doesn't change the distribution mod 6.
And if the distribution is uniform modulo k, then it's uniform modulo m for any m|k, because you take an equal number of groups together (k/m).
|
|
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
william wu
wu::riddles Administrator
Gender:
Posts: 1291
|
|
Re: Dice sum divisibility
« Reply #6 on: Oct 17th, 2008, 9:46am » |
Quote Modify
|
Problem 0)
Here's a long way of saying the same thing towr said ... just my own way of seeing it. Have not got to the other problems yet.
To show that S_n is uniformly distributed mod m, it suffices to show that S_2 is uniformly distributed mod m. We can then deduce a uniform distribution for any larger sums by induction.
Let X be a random variable describing the outcome of the first roll of the die, and Y denote the outcome of the second roll. Then S_2 = X+Y. Now imagine making a 6x6 matrix that enumerates all the possible ways sums can be made from X and Y. The rows are decorated with the possible values of X, and the columns are decorates with the possible values of Y. Then for i  {1,2,3,4,5,6} and j {1,2,3,4,5,6}, the ij-th entry of the matrix contains i + j:
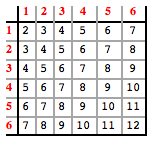
We can make the matrix is Toeplitz by reversing the ordering of the columns, so that instead of the jth column representing Y=j, it will now represent Y = 6-j+1. Then
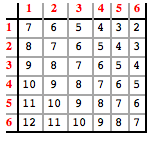
Now, the ij-th entry contains (6 - j + 1) + i = (i-j) + (6+1), a function of (i-j), which indicates that the matrix is Toeplitz.
Lastly, let m be any factor of 6, and take residues of our Toeplitz matrix mod m. For example, if m=6, the matrix of residues is
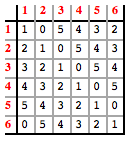
The ij-th entry is now
( (i-j) + (6+1) ) mod 6 = ((i-j) + 1) mod 6
a function of (i-j) mod 6, which makes this a circulant matrix. Thus, to assure that every entry in a circulant matrix appears the same number of times, it suffices to show that every entry in the first column appears an equal number of times. Setting j=1, we get that the ith entry of the first column is:
i mod 6 : i {1,2,3,4,5,6}
and thus all numbers in {0,1,2,3,4,5} appear exactly once, proving that we have an uniform distribution mod 6. Similarly, if m is any factor of 6, and we take residues mod m, then the ith entry of the first column is
i mod m : i {1,2,3,4,5,6}
and since m | 6, every possible residue will occur the same number of times; namely, (6/m) times.
To show that the result holds as well for a die with k sides, just replace all instances of 6 above with k.
|
| « Last Edit: Oct 17th, 2008, 9:50am by william wu » |
IP Logged |
[ wu ] : http://wuriddles.com / http://forums.wuriddles.com
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print