Author |
Topic: tough number theory prob. (Read 3014 times) |
|
Grimbal
wu::riddles Moderator
Uberpuzzler
Gender: 
Posts: 7527
|
 |
Re: tough number theory prob.
« Reply #25 on: Oct 18th, 2008, 11:54pm » |
 Quote  Modify
|
The way I see it is that the correct notation is:
a  b (mod n)
and it should be understood as
a b (please understand as the equivalence modulo n)
So, "(mod n)" is not part of the expression, but gives a context to it.
The equivalence
a b (mod n)
means
a = b + k·n for some k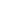  
which implies
rem(a,n) = rem(b,n)
This has nothing to do with the binary operator 'mod' that you can see in some computer languages.
In mathematics you use " ... (mod n)" equivalence and express the remainder with a rem(x,n) function, while in some computer languages, or calculators, you use "mod" as an operator to compute a remainder.
|
|
 IP Logged |
|
|
|
Michael Dagg
Senior Riddler
Gender:
Posts: 500
|
|
Re: tough number theory prob.
« Reply #26 on: Nov 7th, 2008, 12:23pm » |
Quote Modify
|
Nice discussion and as pointed out, this is an interesting
problem as well as ones like it. It is crucial in many problems
to know the group of units in an algebraic number field.
(For example, when "ideals", then viewed as "ideal numbers" were
first invented by Kummer, it was in the context of proving Fermat's
Last Theorem. He got as far as calculating that some important
ideal would be principal, but then had to wrestle with the possible
ways that the generator could be presented; the options differ
from one another by multiplication by a unit. So it was very
important to know the group of units in those algebraic number
fields.)
A summary of what happens is that the group of units in the
ring of integers in an algebraic number field F is a
finitely-generated abelian group, (that's not obvious!) hence (easy)
it's isomorphic to a finite group T times a free abelian group Z^r .
The finite subgroup T is (easy) the group of roots of unity that
lie in the field, and that' not usually hard to determine; at worst
you have to try factoring a finite list of cyclotomic polynomials
like x^n - 1 over the field. The torsion-free part can be shown
to be of rank s1+s2 where s1 is the number of embeddings of the
field into the real numbers, and s2 is the number of complex-conjugate
pairs of non-real embeddings. (These numbers make s1 + 2 s2 = [ F : Q ] .)
The calculation of this value of r is a little bit clever but not
hard to follow. The hardest part of all is to actually compute a set
of r generators of this group; typically one can find a set of r
independent units, i.e. one can find a group of units which is of
finite index in the full group of units, but then you have to decide
whether for example any simple combination of the units you know is
the square of another unit you didn't previously know about.
I like the book Number Theory by Borevich and Shafarevich (despite its
numerous misprints and lousy index) because it treats all these topics.
Definitely one to add to your bookshelf.
|
| « Last Edit: Nov 7th, 2008, 12:24pm by Michael Dagg » |
IP Logged |
Regards,
Michael Dagg
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print