 Author
Author |
Topic: A doublecheck on Peano (Read 2833 times) |
|
Mickey1
Junior Member
 

Gender: 
Posts: 116
|
 |
A doublecheck on Peano
« on: Apr 29th, 2012, 12:48pm » |
 Quote Quote  Modify Modify
|
Peano´s axioms are said to define the arithmetical properties of natural numbers, that is they say something about natural numbers. This seems to rule out the additional task of also defining natural numbers, since they are assumed to exist at the outset. One issue is the distance between numbers, that is 1, which also has the property that 1*n=n, an important property.
But would not the axioms also apply to the series 0,2,4,6,8..,2n,.., or 0, 3, 6 9 … 3n, or any other such subset of natural numbers? Observe also that all the 9 axioms seem to be involved and relevant for these series. Would we not benefit from a logical system defining the natural numbers?
Here is the checklist:
1. 0 is a natural number.
2. For every natural number x, x = x.
3. For all natural numbers x and y, if x = y, then y = x.
4. For all natural numbers x, y and z, if x = y and y = z, then x = z.
5. For all a and b, if a is a natural number and a = b, then b is also a natural number.
6. For every natural number n, S(n) is a natural number.
7. For every natural number n, S(n) = 0 is False.
8. For all natural numbers m and n, if S(m) = S(n), then m = n.
9. If K is a set such that:
a. 0 is in K, and
b. for every natural number n, if n is in K, then S(n) is in K,then K contains every natural number.
|
|
 IP Logged IP Logged |
|
|
|
pex
Uberpuzzler
    

Gender: 
Posts: 880
|
 |
Re: A doublecheck on Peano
« Reply #1 on: Apr 29th, 2012, 1:26pm » |
 Quote Quote  Modify Modify
|
on Apr 29th, 2012, 12:48pm, Mickey1 wrote:| But would not the axioms also apply to the series 0,2,4,6,8..,2n,.., or 0, 3, 6 9 … 3n, or any other such subset of natural numbers? Observe also that all the 9 axioms seem to be involved and relevant for these series. |
|
I think this list of axioms holds for every countably infinite set, with suitable definitions of '0' and 'S'. Which is a good thing, really - we don't want an isomorphism taking us from a set in which the axioms hold to a set in which they don't hold.
|
|
 IP Logged IP Logged |
|
|
|
0.999...
Full Member
  

Gender: 
Posts: 156
|
 |
Re: A doublecheck on Peano
« Reply #2 on: Apr 29th, 2012, 8:29pm » |
 Quote Quote  Modify Modify
|
Specifically, if we assume the existence a set containing all natural numbers (e.g. the axiom of infinity guarantees that), then for such a set N, choose an element a, and define S: N->N-{a} such that S is a bijection. The axiom which states that (N,S) = ( ,_+1) iff the equality holds inductively shows that indeed we are fine choosing any countably infinite N. ,_+1) iff the equality holds inductively shows that indeed we are fine choosing any countably infinite N.
The only reason why N must have cardinality 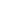 0 is that induction as stated in the axiom list you posted is restricted to successors. A generalization of such induction is transfinite induction which allows us to speak of any ordinal as being equivalent to a well-ordered set when all corresponding initial segments are isomorphic. 0 is that induction as stated in the axiom list you posted is restricted to successors. A generalization of such induction is transfinite induction which allows us to speak of any ordinal as being equivalent to a well-ordered set when all corresponding initial segments are isomorphic.
|
| « Last Edit: Apr 30th, 2012, 6:13am by 0.999... » |
 IP Logged IP Logged |
|
|
|
Mickey1
Junior Member
 

Gender: 
Posts: 116
|
 |
Re: A doublecheck on Peano
« Reply #3 on: May 1st, 2012, 8:47am » |
 Quote Quote  Modify Modify
|
I guess your answer is no.
|
|
 IP Logged IP Logged |
|
|
|
0.999...
Full Member
  

Gender: 
Posts: 156
|
 |
Re: A doublecheck on Peano
« Reply #4 on: May 1st, 2012, 11:09am » |
 Quote Quote  Modify Modify
|
I am sorry for such a confusing answer. My intent was to confirm that you are correct and extend it.
The context, which I failed to mention, was that set-theory can act as a background for the definition of natural numbers. For instance, any of those enumerations you gave (0,3,...3n,...) make sense (to me) only as sets. One huge benefit of doing this is that those equality axioms you have listed (e.g. a=b implies b=a) follow from the Axiom of Extensionality. Thus, we only have to worry about the set itself (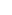 ) and the successor function obeying the Peano Axioms. ) and the successor function obeying the Peano Axioms.
The successor function has to be a bijection 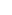 -> -> 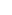 -{0}, as you can verify. Using this, we see that -{0}, as you can verify. Using this, we see that 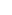 must be infinite. But, there is seemingly a circularity: the definition of a set being infinite means that it is not one-to-one onto a subset of the natural numbers. Thus, I avoided that by assuming the Axiom of Infinity and assumed must be infinite. But, there is seemingly a circularity: the definition of a set being infinite means that it is not one-to-one onto a subset of the natural numbers. Thus, I avoided that by assuming the Axiom of Infinity and assumed 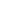 , { , {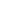 }, { }, {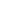 ,{ ,{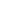 }}, ... represented the finite natural numbers. Then any countably infinite set is defined to be one-to-one onto the set of all these, which can be called }}, ... represented the finite natural numbers. Then any countably infinite set is defined to be one-to-one onto the set of all these, which can be called  . I went on to show that any countably infinite set, containing an element a, and any bijection from that set to itself without {a} is a representative of the natural numbers by Peano's definition. . I went on to show that any countably infinite set, containing an element a, and any bijection from that set to itself without {a} is a representative of the natural numbers by Peano's definition.
For instance, if we define 0 = 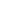 , 1 = {0}, n+1 = S(n) = {n} = {...{ , 1 = {0}, n+1 = S(n) = {n} = {...{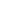 }...}, then the set of all n represents the natural numbers. }...}, then the set of all n represents the natural numbers.
Now, define for all natural numbers n and m, n < m if and only if S(n) < m or S(n) = m. This ordering relation well-orders the natural numbers, and it makes sense to talk about well-ordered sets like the natural numbers, but in general larger than the natural numbers. These are members of the class of Ordinal numbers. My point was that you can represent any given ordinal number by many candidates.
|
| « Last Edit: May 1st, 2012, 12:02pm by 0.999... » |
 IP Logged IP Logged |
|
|
|
Mickey1
Junior Member
 

Gender: 
Posts: 116
|
 |
Re: A doublecheck on Peano
« Reply #5 on: May 6th, 2012, 2:37pm » |
 Quote Quote  Modify Modify
|
I still insist on an axiomatic description of the natural numbers.
However, I first note that the number series defined as natural can be just about anything, not only 0,2,4…For example consider the sequence defined by Pi-3; 0,141..
Let 0 be the first natural number and 0,1 the next, then 0,04, then 0,001 the next etc. These definitions and the sequence are consistent with all the requirements of the Peano axioms unless you require that the numbers are known or accepted in advance (which he perhaps did).
I also note that the capacity for proof of induction offered by the axioms themselves is very modest. The only thing that can be proved is related to the characteristics of the set K. Almost the only property available for a subsequent proof is that n is a natural number since n being such a number implies that S(n) also is a number and the first number also belong to K. Therefore the natural numbers are natural numbers. (Perhaps also some the other axioms can be proved by induction: that S(n) is not equal to n, if n is a natural number, and S(S(n)) is different from S(n). ) The power of induction is completely related to the introduction of addition and multiplication.
I now also see that Wikipedia (not Peano) offers more of what I am looking for, further on in the same article on Peano’s axioms, as a complement to the axioms: “The Peano axioms can be augmented with the operations of addition and multiplication….”
However, in the treatment of these new concepts I believe a few axioms are missing - some related to the fact that S(0) is defined as 1.
• S(0)*n=n (that is 1*n=n) for all n. (This explains also that 0*n=0 since 1*n=( 0+1)*n = 0*n+1*n implying that 0*n=0, since 0+1*n=0*n+1*n)
I also think you need the extra axioms that
• S(n)=n+1, needed to avoid 0,2,4 etc. being all the natural numbers. Wikipedia just assumes this without any axiom.
This axiom may be used together with the induction axiom to prove that n+m is a natural number if n and m are natural numbers) but we still need the axiom:
• if n and m are natural numbers, then n*m is a natural number (for which the symbols "=" and "S(n*m)" may have relevance).
If these are added to Wikipedia's, I believe we have an axiomatic description of the natural numbers, along with addition and multiplication.
|
| « Last Edit: May 6th, 2012, 2:55pm by Mickey1 » |
 IP Logged IP Logged |
|
|
|
pex
Uberpuzzler
    

Gender: 
Posts: 880
|
 |
Re: A doublecheck on Peano
« Reply #6 on: May 7th, 2012, 2:18am » |
 Quote Quote  Modify Modify
|
on May 6th, 2012, 2:37pm, Mickey1 wrote:I still insist on an axiomatic description of the natural numbers.
However, I first note that the number series defined as natural can be just about anything, not only 0,2,4…For example consider the sequence defined by Pi-3; 0,141..
Let 0 be the first natural number and 0,1 the next, then 0,04, then 0,001 the next etc. These definitions and the sequence are consistent with all the requirements of the Peano axioms unless you require that the numbers are known or accepted in advance (which he perhaps did).
I also note that the capacity for proof of induction offered by the axioms themselves is very modest. The only thing that can be proved is related to the characteristics of the set K. Almost the only property available for a subsequent proof is that n is a natural number since n being such a number implies that S(n) also is a number and the first number also belong to K. Therefore the natural numbers are natural numbers. (Perhaps also some the other axioms can be proved by induction: that S(n) is not equal to n, if n is a natural number, and S(S(n)) is different from S(n). ) The power of induction is completely related to the introduction of addition and multiplication.
I now also see that Wikipedia (not Peano) offers more of what I am looking for, further on in the same article on Peano’s axioms, as a complement to the axioms: “The Peano axioms can be augmented with the operations of addition and multiplication….”
However, in the treatment of these new concepts I believe a few axioms are missing - some related to the fact that S(0) is defined as 1.
• S(0)*n=n (that is 1*n=n) for all n. (This explains also that 0*n=0 since 1*n=( 0+1)*n = 0*n+1*n implying that 0*n=0, since 0+1*n=0*n+1*n)
I also think you need the extra axioms that
• S(n)=n+1, needed to avoid 0,2,4 etc. being all the natural numbers. Wikipedia just assumes this without any axiom.
This axiom may be used together with the induction axiom to prove that n+m is a natural number if n and m are natural numbers) but we still need the axiom:
• if n and m are natural numbers, then n*m is a natural number (for which the symbols "=" and "S(n*m)" may have relevance).
If these are added to Wikipedia's, I believe we have an axiomatic description of the natural numbers, along with addition and multiplication. |
|
I'm definitely not an expert on axiomatic number theory, but let's give it a go.
The axioms that you propose, follow immediately from the definitions of addition and multiplication, which are (from the wiki article):
Addition: the function from NxN to N with a + 0 = a and a + S(b) = S(a+b) for all a,b.
Multiplication: the function from NxN to N with a * 0 = 0 and a * S(b) = a + (a * b) for all a,b.
So, once you've properly defined the symbols that you're using in your proposed axioms, it seems that they become superfluous.
|
|
 IP Logged IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: A doublecheck on Peano
« Reply #7 on: May 7th, 2012, 2:59am » |
 Quote Quote  Modify Modify
|
When you talk about natural numbers as 0, s(0), s(s(0)) etc, labels like 1,2,3,4 are all just that, labels. There is no problem labeling 0,s(0), s(s(0)) as 0,2,4. However, in that context there is no 1 or 3, because if you say the successor of 0 is 2, there can not be another number in between -- otherwise 2 would not be the successor of 0.
If you first change the meaning of the labels, and then confuse them with the regular meanings of those labels you shouldn't be surprised it results in nonsense.
Quote:You've got that backwards, 1 is conventionally defined as the successors of 0. And for that matter, the Romans called it "i".
Quote:| S(0)*n=n (that is 1*n=n) for all n. |
|
This doesn't add anything, since it already follows from the given axioms for addition and multiplication:
S(0)*n
<=> {M2}
n + 0*n
<=> {M1}
n + 0
<=> {A1}
n
therefore s(0) * n = n for all natural numbers n
Quote:This also follows from the given axioms already. Except that you're confusing what '1' means. 1 is, in this context, nothing more than a convenient label for s(0).
n+s(0)
<=> {A2}
s(n + 0)
<=> {A1}
s(n)
therefore s(n) = n + s(0) for all natural numbers n
It is not a problem if you label the natural numbers 0,2,4,6,8 etc; so it is not anything you need to prevent using an axioms. And trying to do it the way you seem to desire would entail having to define the decimal system alongside the natural numbers, rather than just describing the natural numbers. (Because what is 1? what is 2? You never said; it's not part of the logic.)
If the natural numbers were labeled 0,2,4,6,8 etc, then 4*6 would simply be 12 (the sixth successor of 0, because 4 and 6 are the second and third). This is only a change of labels, not of meaning. It's really no more problematic than saying 6decimal = 110binary. Or if we drop the explanation subscript, 11*11 = 1001.
It only appears to be wrong, because the default assumptions about what the labels mean are incorrect.
|
| « Last Edit: May 7th, 2012, 3:04am by towr » |
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Mickey1
Junior Member
 

Gender: 
Posts: 116
|
 |
Re: A doublecheck on Peano
« Reply #8 on: May 7th, 2012, 4:13am » |
 Quote Quote  Modify Modify
|
I see now that we need less extra axioms.
I actually started with even more. I simply didn't understand how 1 was defined. I understand the issue of labels but I was looking for the unit 1.
(I still think we need the last axiom about a*b. You usually see this in other descriptions of sets. Perhaps it is intended to be included in the phrase "multiplication is the function N × N to N".)
Although I still don't like the real numbers I am now convinced we seem to have a complete system for the natural numbers, including 0.
|
|
 IP Logged IP Logged |
|
|
|
pex
Uberpuzzler
    

Gender: 
Posts: 880
|
 |
Re: A doublecheck on Peano
« Reply #9 on: May 7th, 2012, 4:46am » |
 Quote Quote  Modify Modify
|
on May 7th, 2012, 4:13am, Mickey1 wrote:| I still think we need the last axiom about a*b. You usually see this in other descriptions of sets. Perhaps it is intended to be included in the phrase "multiplication is the function N × N to N". |
|
No, we don't need this. Multiplication is defined in terms of the S(.) function, so that axiom 6 covers it.
|
|
 IP Logged IP Logged |
|
|
|
Mickey1
Junior Member
 

Gender: 
Posts: 116
|
 |
Re: A doublecheck on Peano
« Reply #10 on: May 9th, 2012, 1:23pm » |
 Quote Quote  Modify Modify
|
That is not quite clear to me
http://en.wikipedia.org/wiki/Peano_axioms
defines or introduces multiplication as
a*(S(b)=a+(a*b)
In order to understand what the left hand side, a*(S(b), is you have to know what (a*b) on the right hand side is, including (a*b) being a number. Can we assume more than a and b being numbers?
|
|
 IP Logged IP Logged |
|
|
|
rmsgrey
Uberpuzzler
    

    
Gender: 
Posts: 2873
|
 |
Re: A doublecheck on Peano
« Reply #11 on: May 10th, 2012, 4:58am » |
 Quote Quote  Modify Modify
|
on May 9th, 2012, 1:23pm, Mickey1 wrote:That is not quite clear to me
http://en.wikipedia.org/wiki/Peano_axioms
defines or introduces multiplication as
a*(S(b)=a+(a*b)
In order to understand what the left hand side, a*(S(b), is you have to know what (a*b) on the right hand side is, including (a*b) being a number. Can we assume more than a and b being numbers? |
|
But (a*b) is either (a*0) or (a*S(c)) for some c. Since N is well-founded, (a*b) eventually evaluates as a+(a+(a+(...+(a+(a*0))...))). (a*0) is a number by definition, and a+n is a number for any number n, so a*b is known to be a number.
|
|
 IP Logged IP Logged |
|
|
|
Mickey1
Junior Member
 

Gender: 
Posts: 116
|
 |
Re: A doublecheck on Peano
« Reply #12 on: May 10th, 2012, 2:00pm » |
 Quote Quote  Modify Modify
|
I see your point. That was perhaps was Pex meant.
|
|
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register