Rule Name: Identity Introduction (= Intro)
Type of sentences you can prove: Self-Identity (a=a, b=b, c=c, …)
Types of sentences you must cite: None
Instructions for use: Introduce a Self-Identity on any line of a proof and cite nothing, using the rule = Intro.

Rule Name: Identity Elimination (= Elim)
Types of sentences you can prove: Any sentence using at least one name Large(a), Smaller(b, c), Home(max), etc.
Types of sentences you must cite: 1) Identity and 2) A sentence you are replacing a name in, that uses at least one of the names from the identity sentence cited.  Always cite just two prior lines.
Instructions for use: Introduce a sentence on any line of a proof that changes one or more occurrences of a name from a previous sentence.  Cite that sentence you are changing, and cite the identity sentence that says the change you are making is legitimate.

Rule Name: Conjunction Introduction (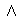 Intro)
Type of sentence you can prove: A Conjunction
Types of sentences you must cite: Any.  May cite as many prior lines as you like, and each will be a conjunct.
Instructions for use: Introduce a new conjunction on any line of a proof by citing each of the conjuncts from prior lines.  These conjuncts must be alone on the line cited.

Rule Name: Conjunction Elimination (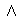 Elim)
Types of sentences you can prove: Any
Type of sentence you must cite: Cite one conjunction only.
Instructions for use: Remove a conjunct from a previous line containing a conjunction.

Rule Name: Disjunction Introduction (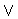 Intro)
Type of sentence you can prove: A Disjunction
Types of sentences you must cite: Any.  Cite only one prior line, it will be a disjunct.
Instructions for use: You can cite any prior sentence available and create a disjunction containing as one conjunct the prior line cited and as another disjunct any sentence you like.

Rule Name: Disjunction Elimination (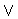 Elim)
Types of sentences you can prove: Any
Types of sentences you must cite: Must cite one disjunction, a subproof for each disjunct within that disjunction, and nothing else.
Instructions for use: Cite a disjunction, create a subproof for each disjunct that begins with each disjunct in turn.  End each subproof with the exact same goal, and then that identical goal sentence is justified outside of the subproofs.

Rule Name: Negation Elimination (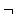 Elim)
Types of sentences you can prove: Any
Types of sentences you must cite: Cite only a negation of a negation.
Instructions for use: If there is a sentence with at least two negations on it, you can take the negations off, two at a time, with this rule.  Cite only one sentence.

Rule Name: Negation Introduction (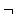 Intro)
Types of sentences you can prove: Any
Types of sentences you must cite: Cite only a single subproof that begins with the opposite of what you hope to prove and ends with  .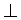
Instructions for use: Begin a subproof with the opposite of what you want to prove outside of the subproof.  End the subproof with 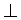 .  Cite only the subproof.

Rule Name: Contradiction Introduction (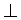 Intro)
Types of sentences you can prove: 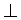 only
Types of sentences you must cite: 1) A sentence, and 2) Exactly that sentence, negated.  Cite only two sentences.
Instructions for use: Find a sentence and it's negation. Cite both and write 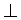 on a line.

Rule Name: Contradiction Elimination (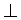 Elim)
Types of sentences you can prove: Any
Types of sentences you must cite: You must cite only a single line containing  .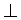
Instructions for use: If you prov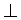e  on a line you may cite that line and write any sentence you please on a subsequent line.

Rule Name: Conditional Introduction (-> Intro)
Types of sentences you can prove: Only a Conditional
Types of sentences you must cite: You must cite only a single subproof.
Instructions for use: To prove a conditional statement, make a subproof that begins with the antecedent and ends with the consequent.

Rule Name: Conditional Elimination (-> Elim)
Types of sentences you can prove: Any
Types of sentences you must cite: You must cite exactly two sentences, 1) a conditional and 2) a sentence that is the antecedent of the conditional in 1).
Instructions for use: You can only prove the consequent of the conditional cited in 1) above.

Rule Name: Biconditional Introduction (<-> Intro)
Types of sentences you can prove: Only a Biconditional
Types of sentences you must cite: You must cite exactly two subproofs.
Instructions for use: To prove a biconditional statement, make a subproof that begins with the left and ends with the right and make another subproof that begins with the right and ends with the left.

Rule Name: Biconditional Elimination (<-> Elim)
Types of sentences you can prove: Any
Types of sentences you must cite: You must cite exactly two sentences, 1) a Biconditional and 2) a sentence that is either the left or right side of the biconditional in 1).
Instructions for use: You prove one side of the biconditional cited in 1) above.

Con Rule Name: Taut Con
Types of sentences you can prove: Any
Types of sentences you must cite: Any/Varies
Instructions for use: Only use to prove things based merely on the logic of connectives, things that could be done with our other normal rules (minus the identity rules).

Con Rule Name: FO Con
Types of sentences you can prove: Any
Types of sentences you must cite: Any/Varies
Instructions for use: Only use to prove things based merely on the logic of connectives and identity, things that could be done with our other normal rules including the identity rules.  (If the sentence could be proven without identity rules, use Taut Con instead.)

Con Rule Name: Ana Con
Types of sentences you can prove: Any
Types of sentences you must cite: Any/Varies
Instructions for use: Use to prove things that are true based on the meanings of the predicates in Tarski's World, and that cannot be proven with any other normal rule or Con rule.

Rule Name: Reit
Types of sentences you can prove: Any
Types of sentences you must cite: Any/Varies
Instructions for use: Allows you to simply REITerate, or repeat, any prior available line with no changes whatsoever.  Remember, lines from previously completed subproofs may not be reiterated.