Andrea has always bought big cars in the past. Big cars are usually gas-guzzlers. So Andrea probably now has a gas-guzzler.
You think of your conclusion, that Andrea now has a gas-guzzler as merely a probable inference. It's not one you would bet your life on. Inductive reasoning turns out to be complicated and we are luckily going to spend most of our time on deductive arguments. Here's an example of a deductive argument. Suppose that you recall that either James Madison or Benedict Arnold was once president of the United States, but you can't remember which. Some knowledgeable person tells you that Benedict Arnold was never president, but was instead a famous traitor. Based on this, you conclude that Madison was once president. Your argument goes:
Madison or Arnold was a president. Arnold was not a president. Therefore, Madison was a president.
Most non-philosophers will use the terms 'valid' and 'sound' interchangeably. By saying, "That's a valid argument." or "Her reasoning is sound." they really mean the same thing, something like "What was said sounds right to me." or something like that. We also say things like "Your Fall parking permit is now invalid." by which we mean it is expired. We aren't talking about logic or arguments at all in such cases. Philosophers, on the other hand, use these terms in a very particular way. Much of what we'll do in this course involves analyzing the arguments made by various philosophers, and we'll be interested in deciding whether those arguments are valid and sound in the senses used by philosophers.
An argument is valid if, and only if, there is no logically possible situation in which all of its premises are true and its conclusion false. Validity then has mainly to do with the form of the argument. Its form needs to be such that if we plugged in true premises we would always get out a true conclusion. An important thing to note here is that the actual truth or falsity of the premises and even the conclusion, is not relevant to whether or not the argument is valid. We will call an argument valid in the cases where if it were to have true premises the conclusion would also have to be true, without worrying about whether the premises are in fact true. (We will be interested in that too, but just not when determining validity of arguments.) Let's look at some examples of valid and invalid deductive arguments:
Key:
M: "Madison was a president." (True. James Madison was
the 4th president.)
A: "Arnold was a president." (False. Benedict Arnold was a
famous traitor, not a president.)
L: "Lee was a president." (False. Robert E. Lee was a famous
Confederate general, not a president.)
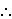 Three dots arranged like this is an
abbreviation for "Therefore"
Three dots arranged like this is an
abbreviation for "Therefore"
(Note that you don't actually need to know these historical facts to
determine validity. If you understood the definition of validity,
you know why.)
| M or A | True | L or A | False | If A then M | True | ||
| not A | True | not A | True | A | False | ||
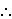 M M |
True | 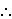 L L |
False | 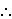 M M |
True | ||
| Valid | Valid | Valid |
So we can have valid arguments with all true premises and a true
conclusion, not all true premises and a false conclusion, or not all
true premises and a true conclusion. The only thing we cannot have, if
an argument is valid, is all true premises and a false conclusion. What
about invalid arguments? The following are all invalid:
| M or A | T | M | T | M or A | T | A or L | F | |||
| M | T | not A | T | A | F | M | T | |||
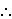 A A |
F | 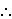 not L not L |
T | 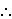 M M |
T | 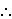 L L |
F | |||
| Invalid | Invalid | Invalid | Invalid |
The moral of the story is that you can have any combination of truth values across premises and conclusion and the argument may still be invalid. This will be because the form of the argument is flawed. Validity then, is all about form.
Validity by itself isn't all we want to know about an argument
though. We are also interested in the 'soundness' of arguments.
An argument is sound if, and only if, it 1) is valid, and 2) has
all true premises.
Soundness then, is a much more interesting notion, for if we know an
argument is valid, we still don't know if we can rely on its conclusion,
but if we know an argument is sound, then we can be certain that its
conclusion is true.
Try these exercises:
Indicate whether each of the following arguments is valid (V) or
invalid (I) then indicate whether each is sound (S) or unsound
(U). (Hint: It may help to sketch the logical form of the
argument. If you are unsure of any of these facts, I'll explain.)
| V/I | S/U | |
| 1. Michael Jackson was assassinated or was killed in an
accident. Michael Jackson was not killed in an accident. Therefore, Michael Jackson was assassinated. |
||
| 2. Princess Diana was assassinated or was killed in an
accident. Princess Diana was not assassinated. Therefore, Princess Diana was killed in an accident. |
||
| 3. Princess Diana was assassinated or was killed in an
accident. Princess Diana was killed in an accident. Therefore, Princess Diana was assassinated. |
||
| 4. Michael Jackson was not shot by a lunatic. Princess Diana was not shot by a lunatic. Therefore, John Lennon was shot by a lunatic. |
||
| 5. If Princess Diana was assassinated then the world
mourned her death. Princess Diana was assassinated. Therefore, the world mourned her death. |
||
| 6. Princess Diana was shot by a lunatic or Michael Jackson
was shot by a lunatic. John Lennon was shot by a lunatic. Therefore, Michael Jackson was shot by a lunatic. |
||
| 7. Princess Diana was killed in an accident or Michael
Jackson was killed in an accident. Michael Jackson was killed in an accident. Therefore, Princess Diana was killed in an accident. |