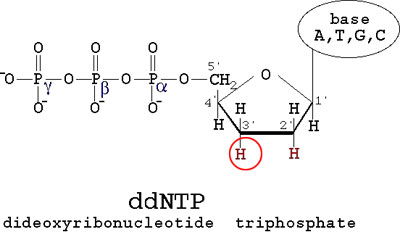
DNA Sequencing

After the finding that DNA's information was encoded in its sequence of nucleotides (A, C, T, and G), it was believed that one could find this sequence through a method of analyzing a large number of identical strands of DNA and identifying each nucleotide in order of it's appearance in the DNA sequence. This technique was ultimately discovered in 1977 by Fredrick Sanger. His method, known as Sanger Sequencing, relied on two main principles.

DNA can be separated by size. This was briefly discussed in the section on Laboratory Techniques with regards to gel electrophoresis. Keeping in mind that DNA is negatively charged, it will migrate towards the positive electrode when an electric current is applied. When placed in a gel composed of polyacrylamide beads, larger strands of DNA will migrate through the gel slower. Incidentally, the use of polyacrylamide gels instead of agarose gels allow for much greater resolution in separating strands of DNA by size. It allows one to actually distinguish a strand of DNA 400 base pairs long from a strand of DNA 401 base pairs long. As a result, polyacrylamide gels would be capable of resolving even 1 base pair differences in DNA, making this very useful for sequencing.

In addition, the chemical structure of DNA allows geneticists to manipulate its normal function and use it to identify the sequence of a strand of DNA. As was discussed in the section about DNA replication, cells have a protein called DNA Polymerase II that adds nucleotides complementary to the original strand, allowing it to form two identical strands of DNA from a template strand. To do this, it adds one nucleotide complementary to the template strand at a time. In order to do this, Polymerase requires a DNA Primer, a short strand of DNA complementary to the end of the template strand for a 3' OH group. The following diagram shows the structure of a normal nucleotide (dNTP):

DNA Polymerase II normally will connect the 3' OH to the next nucleotide at the 5' Phosphate group, labeled alpha, and kick off Phosphates beta and gamma. DNA primers provide the 3' OH for DNA Polymerase to build onto. It was realized that without that 3' OH group, the strand could no longer be elongated, which provided the basis for the Sanger Sequencing technique. Sanger proposed the synthesis of a modified form of a nucleotide, a dideoxyribonucleotide triphosphate (ddNTP), which share the same structure as a normal dNTP, with the exception of the 3' OH group, which is replaced by an H:

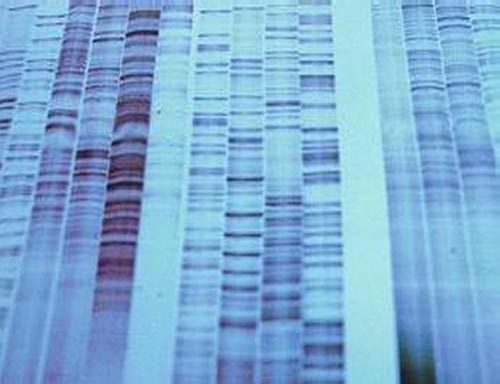
DNA Polymerase would be able to integrate this modified nucleotide if added in vitro (in a test tube outside the cell) and would immediately terminate the chain being synthesized, as the lack of a 3' OH group would prevent any further addition of nucleotides to the synthesizing strand. This resulted in the discovery of the first technique of DNA sequencing.

Four separate reaction tubes would be required, each one containing radioactively labeled DNA primers, DNA Polymerase II, and an ample amount of all 4 dNTP (dATP, dTTP, dGTP, dCTP), each to be integrated into the DNA strand being synthesized as a nucleotide. In addition, each reaction tubes would contain a different ddNTP, allowing each tube to identify a different nucleotide along the strand. For example, one tube would contain a ddATP, enabling that reaction tube to identify all the A's being integrated into the synthesizing strand, and thus all the T's in the complementary template strand (recall that T nucleotides are complementary and base pair with A nucleotides). All 4 dNTPs and a different ddNTP are added to each reaction tube in a ratio of around 300:1, and Polymerase will randomly integrate either a dNTP or a ddNTP into the synthesizing strand if the ddNTP complements with the nucleotide on the template strand. As a result, a reacting that has ddATP would integrate a dGTP, dCTP, and dTTP if the template strand's nucleotide was C, G, or A, respectively. If the template strand's nucleotide was T, however, Polymerase will randomly integrate either dATP or ddATP. If it integrates dATP, the strand will continue to synthesize, which is what generally happens 97% of the time. If it integrates a ddATP, however, the reaction for that strand of DNA is terminated immediately, and will be of that size for good. This process is repeated with three other tubes with ddGTP, ddCTP, and ddTTP.

Once this reaction is ran to completion, it is then put onto a flat slab of polyacrylamide gel and an electric current is applied in a process called PolyAcrylamide Gel Electrophoresis. This allows for the separation of strands of DNA one base-pair apart, allowing one to resolve the sequence of the template strand by viewing the gel in a process called Autoradiography. Because the primers added were radioactive, an image of it can be taken, where every time strands of DNA are encountered on the gel, a band appears. The end product is a gel with a banding pattern that looks similar to this:

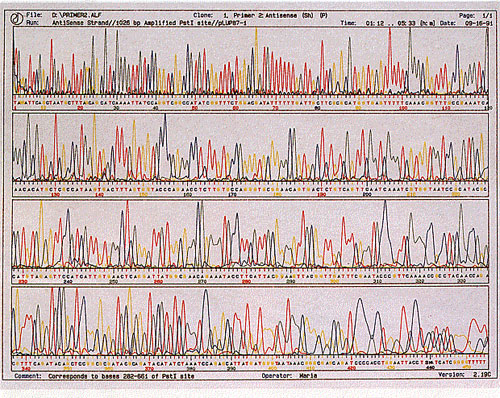
This technique of sequencing, however, has two major shortcomings. The length of the DNA being sequenced cannot be longer than 1000 base pairs long, or it will be completely inaccurate. Typically, sequencing is done on strands of DNA no longer than 850 base pairs long for the best accuracy. This has severe implications for the sequencing of large genomes such as humans, which have a genome of almost 3 billion base pairs!. In addition, this technique of sequencing has another major flaw that one can see from the image above: it requires that the sequences be read by a person. The amount of time it would take for people to manually read and record genomes billions of base pairs long would be impractical for realistic research.

The invention of automated sequencers in 1987 by Applied Biosystems was a breakthrough in the ability of geneticists to sequence large genomes. While the limitation of 1000 base pairs for sequencing is still unavoidable, it solves the problem of needing people to read and record the sequence. In an automated sequencing process, instead of labelling the primers with radioactive labels, the ddNTP is labeled with a fluorescent label, where each ddNTP would fluoresce a different color when a laser is fired through it. Unlike the autoradiography, which will show a band of the same color regardless of the ddNTP, this method will fluoresce a different color for each of the four different nucleotides. Thus, this allows for the sequencing reaction to occur in one tube, as each ddNTP would fluoresce a different color and identify the nucleotide in the sequence. Once the reaction was ran to completion, it was placed into a gel tray where an electric current would be applied from the tray into 96 microcapillaries, all of which will gather at a laser. The idea is that the DNA will migrate towards the positive electrode at the laser end, where it would fluoresce a specific wavelength of light once the DNA passes through, and get recorded by a computer detector. The wavelength of light detected would be automatically associated with the corresponding nucleotide, allowing computers to automatically print out a chromatogram as well as the sequence, similar to this image:

Thus, using computers, the amount of time it takes to sequence strands of DNA is significantly shortened. Without this computing technology, large scale sequencing projects would be impossible to even initiate, much less complete. This paved the way for projects such as the Human Genome Project, which was initiated by the NIH in 1991.

Back to top