(Or, "how do I rotate a bitmap?")
What follows are my own notes on Alan Paeth's ``A Fast Algorithm for General Raster Rotation,'' as published in the proceedings of Graphics Interface '86. This is a very popular algorithm for image rotation, used by many libraries such as ImageMagick, pnmrotate, etc. Initially I hoped that this scheme would be suitable for use in scientific data processing where arrays must be rotated, but now I believe that this scheme is unsuitable due to the poor interpolation. I also question whether this is any faster than bilinear interpolation when run on general purpose hardware (due to the large amount of data movement); however I do not yet have any quantitative measurements. These concerns aside, the decomposition of a rotation into three shears is interesting in its own right. — Tobin 2002-07-07
A two dimensional shear operation axis has the following matrix representations (one shear matrix for a shear parallel to the X axis, and another for a shear parallel to the Y axis):
Shear-X(α)= [1 α ; 0 1 ]
Shear-Y(β)= [1 0 ; β 1 ]
Thus a shear in the X direction produces y':=y (unchanged) and x':=x+αy.
It turns out that any orthogonal transformation can be realised by a combination of a shear along one axis, then a shear along the other axis, followed by another shear along the first axis: (although that is not proved here)
ShearX(α) ShearY(β) ShearX(γ) =
[1 α ; 0 1 ]
[1 0; β 1 ]
[1 γ ; 0 1 ]
= [1+αβ, α+γ+αβγ ; β, 1+βγ ]Doing a rotation by performing three shear operations might be advantageous, because it's easy to do a shear operation. To do a shear operation on a raster image (that is to say, a bitmap), we just shift all the pixels in a given row (column) by an easy-to-calculate displacement. But in order to do a rotation using shears, we'll have to be able to calculate the necessary values of α, β, and γ from the rotation angle Θ.
Recall the familiar rotation matrix:
Rotate(Θ) = [ cos(Θ), -sin(Θ) ; sin(&Theta), cos(&Theta) ]Set the rotation matrix equal to the product of the three shears:
[1+αβ, α+γ+αβγ ; β, 1+βγ ] = [ cos(Θ), -sin(Θ) ; sin(&Theta), cos(&Theta) ]
Solve for α, β, & γ in terms of Θ:
&beta = sin(Θ)
1+αβ=cos(Θ)
1+αsin(Θ)=cos(Θ)
α=(cos(Θ)-1)/sin(Θ)
α=-tan(Θ/2)1+αβ=1+βγ
γ=α
Thus we have α=γ=-tan(Θ/2) and &beta = sin(Θ).
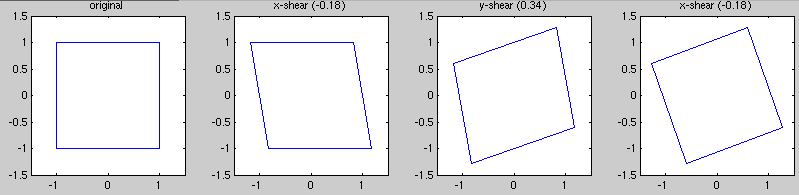
Let Θ=20°. Then α~-0.18 and β~0.34. Here you can see what a square looks like as the three shears are applied:

Just for fun we can superimpose the original box, the intermediate results, and the final image:
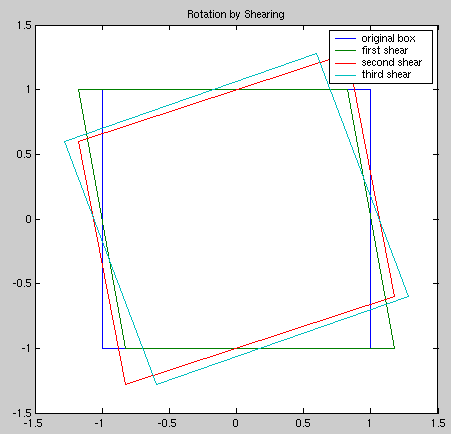
That's it!
Alan Paeth presents code in a Pascal-like language to do a shear in an efficient manner, using a simple approximation to do some interpolation (see his paper for the details of the approximation). Here's the code:
PROCEDURE xshear(shear, width, height)
FOR y:= 0 TO height-1 DO
skew := shear * (y + 0.5);
skewi := floor(skew);
skewf := frac(skew); /* = skew - skewi */
oleft := 0;
FOR x:= 0 TO width-1 DO
pixel := P(width-x, y);
left := pixmult(pixel, skewf);
/* pixel - left = right */
pixel := pixel - left + oleft;
P(width-x+skewi, y) := pixel;
oleft := left;
OD
P(skewi, y) := oleft;
OD
END
You can just replace the pixmult function with multiplication in most cases; its function is just to weight the given pixel value for the "skewf" fraction. The array to be sheared is given as the variable P, and shear is the shear factor (i.e. α, β, or γ). To make this useful you'll have to incorporate a change-of-origin to the center of rotation, and a suitable displacement to deal with negative indicies.
Here's the beginnings of an implementation in matlab: (xshear.m)
function data_out = xshear(data,shear,antialias)
% function data = xshear(data,shear)
%
% $Id: xshear.m,v 1.1 2002/07/06 17:38:37 tobin Exp $
the_size = size(data);
width = the_size(1);
height = the_size(2);
for y=1:height,
skew = shear * y; % how much to shift this line
skewi = floor(skew); % integer part
skewf = skew - skewi; % fractional part
oleft = 0;
for x=width:-1:1, % from right to left...
pixel = data(x, y); % sample the pixel
if antialias,
left = pixel * skewf;
else
left = 0;
end
pixel = (pixel - left) + oleft;
if (x+skewi > 0),
data_out(x+skewi,y) = pixel;
end
oleft = left;
end
if (skewi+1 > 0),
data_out(skewi+1,y) = oleft;
end
end
Tobin Fricke