Putnam 2016 Part 2

Random number: 82

15th December 2016

Here's my cool solution to the third problem of the 2016 Putnam competition:

A3. Suppose that $f$ is a function from $\mathbb{R}$ to $\mathbb{R}$ such that $$f(x) + f(1-\frac{1}{x}) = \text{arctan}(x)$$ for all real $x \neq 0$. (As usual, $y = \text{arctan}(x)$ means $-\pi /2 < y < \pi /2$ and $\text{tan}(y) = x$.) Find $$\int_0^1 f(x) dx$$

So we have that $$f(x) + f(1 - \frac{1}{x}) = \text{tan}^{-1}(x)$$ We can 'replug' it in to the formula again twice however, to get the following two relations: $$f(1 - \frac{1}{x}) + f(\frac{1}{1-x}) = \text{tan}^{-1}(1 - \frac{1}{x})$$ $$f(\frac{1}{1-x}) + f(x) = \text{tan}^{-1}(\frac{1}{1-x})$$ Combining these three equations, we end up with: $$2f(x) = \text{tan}^{-1}(x) - \text{tan}^{-1}(1 - \frac{1}{x}) + \text{tan}^{-1} (\frac{1}{1-x})$$ Then to find $\int_{0}^{1} f(x) \text{d}x$, we can simply integrate each term on the right hand side from 0 to 1 and divide by 2.

First Integral: $$\int_{0}^{1} \text{tan}^{-1}(x) \text{d}x = \frac{\pi}{4} - \int_{0}^{\frac{\pi}{4}} \text{tan}(y) \text{d}y$$ $$=\frac{\pi}{4} + \left[ \text{ln} (\text{cos}(y))\right]_{0}^{\frac{\pi}{4}}$$ $$=\frac{\pi}{4} - \frac{1}{2}\text{ln}(2)$$

Second Integral: $$\int_{0}^{1} \text{tan}^{-1}(1 - \frac{1}{x}) \text{d}x = \int_{-\infty}^{0}\frac{\text{tan}^{-1}(u)}{(1-u)^2}\text{d}u \color{red}{\text{ (Use 'u' substitution)}}$$ $$=\left[ \frac{\text{tan}^{-1}(u)}{(1-u)} \right]^0_{-\infty} - \int_{-\infty}^{0}\frac{1}{(1+u^2)(1-u)}\text{d} u \color{red}{\text{ (Integrate by Parts)}}$$ $$= -\frac{1}{2} \int_{-\infty}^{0} \frac{u + 1}{u^2 + 1} + \frac{1}{1-u} \text{d}u \color{red}{\text{ (Partial Fractions)}}$$ $$= -\frac{1}{2} \left[ \frac{1}{2} \text{ln}(u^2 + 1) + \text{tan}^{-1}(u) - \text{ln}(1-u)\right]_{-\infty}^0$$ $$= \frac{1}{2} (\text{ln}(\frac{\sqrt{u^2+1}}{1-u}) + \text{tan}^{-1}(u)) \rvert_{u = -\infty} \color{red}{\text{ (Simplify the logs into one expression)}}$$ $$ = -\frac{\pi}{4}$$

Third Integral: $$\int_{0}^{1} \text{tan}^{-1}(\frac{1}{1-x})\text{d}x = \int_{1}^{\infty} \frac{\text{tan}^{-1}(u)}{u^2} \text{d}u \color{red}{\text{ ('U' substitution)}}$$ $$=\left[ -\frac{\text{tan}^{-1}(u)}{u} \right]_{1}^{\infty} + \int_{1}^{\infty} \frac{1}{u(1+u^2)} \text{d}u \color{red}{\text{ (Integrate by Parts)}}$$ $$=\frac{\pi}{4} + \int_{1}^{\infty}\frac{1}{u} - \frac{u}{1+u^2} \text{d}u \color{red}{\text{ (Partial Fractions)}}$$ $$=\frac{\pi}{4} + \left[ \text{ln}(\frac{u}{\sqrt{u^2+1}}) \right]_{1}^{\infty} \color{red}{\text{ (Simplify the logs into one expression)}}$$ $$=\frac{\pi}{4} + \frac{1}{2}\text{ln}{2}$$

So all in all, we find that $$\int_{0}^{1} f(x) \text{d}x = \frac{3\pi}{8}$$

Onto the next problem! (~~This is one of the one's I actually got during the Putnam~~ I RESCIND THAT COMMENT COMPLETELY, I MESSED UP MY PROOF I am not worthy of anything... Why am I so bad...)

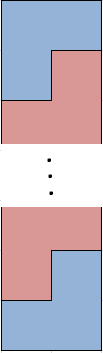
A4. Consider a $(2m-1) \times (2n - 1)$ rectangular region, where $m$ and $n$ are integers such that $m,n \geq 4$. This region is to be tiled using tiles of the two types shown:

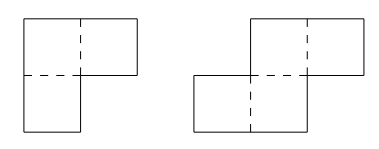
(The dotted lines divide the tiles into $1 \times 1$ squares.) The tiles may be rotated and reflected, as long as their sides are parallel to the sides of the rectangular region. They must all fit within the region, and they must cover it completely without overlapping.

What is the minimum number of tiles required to tile the region?

First, we can color our grid with four colors in the following checkerboard manner:

We can call the two pieces 'three-pieces' and 'four-pieces' based on how many $1 \times 1$ squares make them up. It's obvious that any 'four-pieces' put onto the grid will cover each of the colors once. Each three-piece places will cover three colors once and miss one of the colors.

$$\text{Number of Blue tiles: }mn$$ $$\text{Number of Red tiles: }(m-1)n$$ $$\text{Number of Purple tiles: }m(n-1)$$ $$\text{Number of Green tiles: }(m-1)(n-1)$$
Because the number of tiles are different for each color, it's obvious that we can't only use 'four-pieces'. We need to use 'three-pieces' to equalise the count of each of each color at least. This comes out to at least $$(mn - (m-1)(n-1)) + (mn - (m-1)n) + (mn - m(n-1)) = 2m + 2n - 1$$ 'three-pieces'. Now let's say that we can tile the board with $a$ 'three-pieces' and $b$ 'four-pieces'. Thus we have a lower bound of $a = 2m + 2n -1$. To minimise the number of pieces we use to tile the board, we definitely have to minimise $a$. So if we can achieve this minimum bound, then we are good.

It's obvious to use the minimal number of pieces, we will want to minimise the number of 'three-pieces' that we use. Hence, if we can achieve this lower bound, then life will be good. We can show that we can achieve this lower bound for the base case $m,n = 4$, and then induct on $m,n$:

If we increase $m$ or $n$ by $1$, we are essentially adding a $2$ - width column/row to the rectangular grid, and we also add $2$ to the lower bound of $a$. We can achieve this new lower bound by tiling the extra column like this:

with a 'three-piece' on both ends as caps, we can fill in the rest with 'four-pieces', hence using only two 'three-pieces'. Hence we can fulfil this lower bound on $a$. Working out the number of pieces needed, we find that we need $mn$ pieces to tile the board.