Archimedean absolute values

Posted on September 30, 2019 by rohanjoshi

In the previous post we discussed the Archimedean property for an ordered field. Today I’ll discuss the Archimedean property for valued fields, that is, fields equipped with an absolute value.

Recall that an absolute value on a field $K$ is a function $| \ |: K \to \mathbb{R}_{\geq 0}$ satisfying the following axioms:

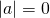$|a| = 0$ if and only if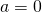 $a = 0$
$|ab| = |a||b|$
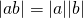
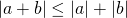$|a+b| \leq |a| + |b|$ (triangle inequality)

for all $a, b \in K$ .

Here is an intuitive, analogous definition for the Archimedean property:

Definition: The absolute value $| \ |$ is Archimedean if, for $x, y \in K$ , $x \neq 0$ , $|nx| > |y|$ for some natural number $n$ .

Clearly the standard absolute value (which is defined on $\mathbb{C}$ and $\mathbb{R}$ , and therefore $\mathbb{Q}$ ) is Archimedean. But wait: since we assumed $x \neq 0$ , we can divide both sides by $|x|$ to obtain $|n| > |y/x|$ . In other words, we can write the definition equivalently as:

Equivalent Definition: The absolute value $| \ |$ is Archimedean if, for all $a \in K$ , $|n| > |a|$ for some natural number $n$ .

Here $a$ takes the place of $y/x$ . The important thing here is that $a$ can be any element of $K.$ So what this is saying is that, given any element of the field, there is some natural number that beats it.

Now, let us assume that the absolute value is nontrivial. (The trivial absolute value has $|a| = 1$ for all nonzero $a$ ). Thus, for some $a$ , $|a| \neq 1$ . So, either $|a| > 1$ or $|1/a| = 1/|a| > 1$ . Thus by taking arbitrarily high powers of $a$ or $1/a$ , we can obtain arbitrarily high absolute values. So we can reformulate the definition as follows:

Equivalent Definition: $| \ |$ is Archimedean if the set $\{ |n| \ | \ n \in \mathbb{N}\}$ contains arbitrarily large elements.

In other words, the set is unbounded. So, $| \ |$ is non-Archimedean if the sequence $|1|, |2|, |3|, \dots$ is bounded. However, if any $|n| > 1$ , then taking arbitrarily high powers of $n$ can give us arbitrarily high absolute values. So

Equivalent Definition: $| \ |$ is non-Archimedean if $|n| \leq 1$ for $n \in \mathbb{N}$ .

Finally, I will present another very useful characterization of the (non)Archimedean property.

Theorem/Equivalent Definition: $| \ |$ is non-Archimedean if $|a+b| \leq \text{max}(|a|, |b|)$ .

Proof: (to be added)

The Archimedean property

Posted on September 30, 2019 by rohanjoshi

If $a$ and $b$ are positive real numbers, if you add $a$ to itself enough times, eventually you will surpass $b$ . This is called the Archimedean property, and it is one of the fundamental properties of the system of real numbers. Informally, what this property says is that no numbers are infinitely larger than others. We can formally define this property as follows:

Let $F$ be an ordered field. We say $F$ is Archimedean if, for $x, y \in F$ where $x, y > 0$ , there exists a natural number $n$ such that $nx > y$ .

An example of a non-Archimedean number system is the hyperreal numbers. Hyperreal numbers are an enlargement of the real numbers that also contain “infinite” and “infinitesimal” quantities. The hyperreal numbers are used to give an alternative formulation of calculus in the subject of non-standard analysis, where instead of using limits, one computes with actual infinitesimals.

More familiar examples of non-Archimedean fields are function fields. For example, consider the field of rational functions (on $\mathbb{R}$ ), denoted $\mathbb{R}(x)$ . We can order rational functions by declaring that

$p > q$ if $p(x) > q(x)$ as $x \to \infty$

for any $p, q \in \mathbb{R}(x)$ . In other words, we order rational functions by looking at their asymptotic behavior. One can check that this satisfies the axioms, making $\mathbb{R}(X)$ an ordered field.

Exercise: Show that a rational function

$p(x) = \frac{f(x)}{g(x)} = \frac{a_nx^n + \cdots + a_1x + a_0}{b_mx^m + \cdots + b_1x + a_0}$

is positive with respect to the order (i.e. $p > 0$ ) if and only if $a_n/b_m > 0$ .

Now one can see that the field of rational functions is clearly not Archimedean. For example, if we consider $p(x) = 1/x$ , no matter how many times we add it to itself, it will never surpass $q(x) = 1$ : the function $np(x) = \frac{n}{x}$ is eventually surpassed by $q(x) = 1$ , no matter how great $n$ is.

Exercise: Define the degree of a rational function to be the degree of its numerator minus the degree of its denominator. For rational functions $p, q > 0$ , show there exists an integer $n$ such that $np > q$ if and only if degree $(p) \geq$ degree $(q)$ .

Thus the basic idea of the Archimedean property is at the core of asymptotic analysis. In defining big-O notation, we write $f(x) = O(g(x))$ if some multiple of $f$ surpasses $g$ as $x$ goes off to infinity.

In the next post, I will discuss the Archimedean property for valued fields (as opposed to ordered fields), and how this applies to number theory.

15 triangles in a web of cubics

Posted on September 11, 2019 by rohanjoshi

Consider a homogeneous cubic form in three variables $X$ , $Y$ , and $Z$ , such as

$X^2Y - X^2Z + XY^2 -XYZ - Y^2Z + Z^3$

Sometimes a cubic form can be factored. In this case, we are lucky: it factors as

$(X-Z)(Y-Z)(X+Y+Z),$

but in general we will not be so lucky. It is pretty rare for a random cubic form to be factorable. From the perspective of projective algebraic geometry, a homogeneous cubic form cuts out an algebraic curve in the projective plane:

and a cubic that factors into three linear forms will cut out three lines: a “degenerate” plane cubic. Such a collection of three lines is called a “triangle”.

The space of homogeneous cubic forms is a 10-dimensional vector space with basis $X^3, X^2Y, X^2Z, Y^3, Y^2X, Y^2Z, Z^3, Z^2X, Z^2Y, XYZ$ . However, given a cubic form $F$ , the scaled form $cF$ corresponds to the same curve. Furthermore, if all the coefficients are zero, then the form doesn’t correspond to the curve at all. Thus the space of plane cubics is nine-dimensional projective space.

In this post we will prove the following enumerative result:

A general three-dimensional family of plane cubics contains exactly 15 triangles.

By a three-dimensional family (aka “web”), we mean some embedded copy of $\mathbb{P}^3$ in this space $\mathbb{P}^9$ of plane cubics. This geometric result corresponds to the following purely algebraic fact:

A general four-dimensional subspace of the ten-dimensional space of cubic forms contains exactly 15 forms which factor into three linear forms.

(I should probably say something about the term “general”. The statement “a general $x \in S$ satisfies property $P$ ” this means that $P(x)$ says that the subset of $S$ for which P(x) holds is dense in $S$ .)

This material is drawn from 3264 And All That by Eisenbud and Harris

The strategy

Let us consider the space of (ordered) triples of lines, or nonzero linear forms up to scaling. This is $\mathbb{P}^2 \times \mathbb{P}^2 \times \mathbb{P}^2$ . We can construct a morphism

$\mathbb{P}^2 \times \mathbb{P}^2 \times \mathbb{P}^2 \to \mathbb{P}^9$

which sends a triple of linear forms $F, G, H$ to their product $FGH$ . This map is (in general) 6 to 1, since there are 6 permutations of three (distinct) linear forms.

We will do intersection theory in $\mathbb{P}^2 \times \mathbb{P}^2 \times \mathbb{P}^2$ : specifically, we will pull back the class of a $\mathbb{P}^3$ in $\mathbb{P}^9$ to $\mathbb{P}^2 \times \mathbb{P}^2 \times \mathbb{P}^2$ , and count how many points it consists of (in other words, how many triples of linear forms correspond to cubic surfaces in a general web). Then we will divide this number by 6, to count the number of triangles in the family.

Computation in the Chow ring

The morphism

$\phi: \mathbb{P}^2 \times \mathbb{P}^2 \times \mathbb{P}^2 \to \mathbb{P}^9$

induces a map of Chow rings:

$\phi^*: A(\mathbb{P}^9) \to A(\mathbb{P}^2 \times \mathbb{P}^2 \times \mathbb{P}^2).$

Now, $A(\mathbb{P}^9) \cong \mathbb{Z}[x]/(x^{10})$ and $A(\mathbb{P}^2 \times \mathbb{P}^2 \times \mathbb{P}^2) \cong \mathbb{Z}[a, b, c]/(a^3, b^3, c^3)$ . The class of any $\mathbb{P}^3$ in $A(\mathbb{P}^9)$ is $x^6$ . Furthermore, $\phi^*(x) = a+b+c$ . So, $\phi^*(x^6) = (a+b+c)^6$ . If we expand this out, removing every term that has any variable to a power of three or greater, we see that every term except the monomial term of $a^2b^2c^2$ vanishes, and its coefficient is the ${6 \choose 2, 2, 2} = \frac{6!}{2!2!2!} = 90$ . $90$ is the the number of ordered triples of linear forms which correspond to cubic forms contained in a general web. Dividing by six, since six ordered triples correspond to one unordered triple (i.e. one distinct triangle), we obtain our answer of 15.