A question I always had when learning linear algebra is, “what does the trace of a matrix mean conceptually?” For example, the determinant of a matrix is, roughly speaking, the factor by which the matrix expands the volume. The conceptual meaning of trace is not as straightforward, but one way to think about it is
trace is the derivative of determinant at the identity.
Roughly you can think of this in the following way. If you start at the identity matrix and move a tiny step in the direction of ![]() , say
, say ![]() where
where ![]() is a tiny number, then the determinant changes approximately by
is a tiny number, then the determinant changes approximately by ![]() times
times ![]() . In other words,
. In other words, ![]() . Here
. Here ![]() stands for the identity matrix.
stands for the identity matrix.
One can be very precise about what it means to take the “derivative” of the determinant, so let me do some setup. Let ![]() be either
be either ![]() or
or ![]() (so we are working with real or complex Lie groups; but of course, everything makes sense for algebraic groups over arbitrary fields). Then there is a morphism of Lie groups called the determinant
(so we are working with real or complex Lie groups; but of course, everything makes sense for algebraic groups over arbitrary fields). Then there is a morphism of Lie groups called the determinant ![]() , given by sending a matrix to its determinant. Since we are restricting to invertible matrices, the determinants are nonzero. To check that this is really a morphism of Lie groups (i.e. both a smooth map and a homomorphism of groups), note that the determinant map is a polynomial map in the entries of the matrix (and therefore smooth) and is a group homomorphism by the property that
, given by sending a matrix to its determinant. Since we are restricting to invertible matrices, the determinants are nonzero. To check that this is really a morphism of Lie groups (i.e. both a smooth map and a homomorphism of groups), note that the determinant map is a polynomial map in the entries of the matrix (and therefore smooth) and is a group homomorphism by the property that ![]() .
.
Now, given any smooth map of manifolds ![]() which maps point
which maps point ![]() , there is an induced linear map on from the tangent space of
, there is an induced linear map on from the tangent space of ![]() to the tangent space of
to the tangent space of ![]() called the derivative of
called the derivative of ![]() at
at ![]() . In particular, if
. In particular, if ![]() is a Lie group homomorphism, then it maps the identity point to the identity point, and the derivative at the identity is furthermore a homomorphism of Lie algebras. What this means is that, in addition to being a linear map, it preserves the bracket pairing.
is a Lie group homomorphism, then it maps the identity point to the identity point, and the derivative at the identity is furthermore a homomorphism of Lie algebras. What this means is that, in addition to being a linear map, it preserves the bracket pairing.
In the case of ![]() , the Lie algebra at the identity matrix is called
, the Lie algebra at the identity matrix is called ![]() . We can think of it as consisting of all
. We can think of it as consisting of all ![]() matrices, and the bracket operation is defined by
matrices, and the bracket operation is defined by ![]() . The Lie algebra of
. The Lie algebra of ![]() at
at ![]() consists of the elements of
consists of the elements of ![]() ; since
; since ![]() is abelian, the bracket is trivial.
is abelian, the bracket is trivial.
The main claim, which I will prove subsequently, is that this map ![]() , the derivative of the determinant at the identity, is actually the trace. That is, it sends a matrix to its trace, the sum of the entries on the diagonal. Note that since it is a homomorphism of Lie algebras, it preserves the bracket, and we recover the familiar property of trace
, the derivative of the determinant at the identity, is actually the trace. That is, it sends a matrix to its trace, the sum of the entries on the diagonal. Note that since it is a homomorphism of Lie algebras, it preserves the bracket, and we recover the familiar property of trace ![]() , so
, so ![]() .
.
We can find the derivative of a smooth map on ![]() directly, since it is an open subset of a vector space. Let
directly, since it is an open subset of a vector space. Let ![]() be a matrix; then the derivative at the identity evaluated at
be a matrix; then the derivative at the identity evaluated at ![]() is
is
![]()
![]() is a polynomial in
is a polynomial in ![]() , and the number we’re looking for is the coefficient of the
, and the number we’re looking for is the coefficient of the ![]() term.
term.
We have
![]()
Just to get a concrete idea of what this expands to, let’s look when ![]() . Then
. Then
![]()
When ![]() ,
,
![]()
![]()
![]()
![]()
![]()
In particular, the coefficient of ![]() is
is ![]() . (In fact, see if you can convince yourself that the coefficient of
. (In fact, see if you can convince yourself that the coefficient of ![]() is
is ![]() .)
.)
See some discussion of the meaning of trace.
Acknowledgements: Thanks to Ben Wormleighton for originally telling me the slogan “trace is the derivative of determinant”, and for teaching me about Lie groups and Lie algebras.
To add: discussion of Jacobi’s formula, exponential map
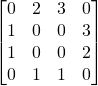 .
.