(These are notes adapted from a talk I gave at the Student Arithmetic Geometry seminar at Berkeley)
Introduction
Probably the most famous open problem in number theory is the Riemann hypothesis. In addition to being worth a million dollars, it is a deep and fundamental problem that has remained intractable since it was first proposed by Bernhard Riemann, in 1859.
The Riemann hypothesis springs out of the field of analytic number theory, which applies complex analysis to problems in number theory, often studying the distribution of prime numbers. The Riemann hypothesis itself has significant implications for the distribution of primes and implies an asymptotic statement about their density (for a precise statement, see here). But the Riemann hypothesis is usually formulated in the language of complex analysis, as a statement about a complex-analytic function, the Riemann zeta function, and its zeroes. This formulation is succint and elegant, and allows the problem to be subsumed into the larger study of the largely conjectural theory of L-functions.
This broader theory allows one to create analogues of the Riemann zeta function and Riemann hypothesis in other contexts. Often these “alternative Riemann hypotheses” are even harder than the original Riemann hypothesis, but there is a famous case where this is fortunately not true.
In the 1940’s, André Weil proved an analogue of the Riemann hypothesis: not for the Riemann zeta function, but for a different zeta function. Here’s one way to describe it: very roughly speaking, the Riemann zeta function is based on the field rational numbers 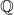 (it can be defined as an Euler product over the primes of
(it can be defined as an Euler product over the primes of 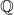 ). Our zeta function will constructed analogously, but instead be based on the field
). Our zeta function will constructed analogously, but instead be based on the field 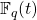 (the field of rational functions with coefficients in the finite field
(the field of rational functions with coefficients in the finite field 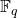 ). So instead of the number field
). So instead of the number field 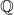 , we have swapped it out and replaced it with a function field.
, we have swapped it out and replaced it with a function field.
Actually, what Weil proved, and what we will prove today, is the analogue of the Riemann hypothesis for global function fields. This work represents the greatest progress we have towards the original Riemann hypothesis, and serves as tantalizing evidence for it.
There is a general pattern in number theory which looks something like the following: start with a problem in number theory. Adapt the problem from the number field setting to the function field setting. Then interpret the function field as the function field of a curve (usually), and then use techniques of algebraic geometry (for example, 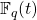 is the function field of a line over
is the function field of a line over 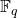 ). That is exactly what we will do here: it will therefore look less like complex analysis and more like algebraic geometry
). That is exactly what we will do here: it will therefore look less like complex analysis and more like algebraic geometry
Math (somewhat rushed)
Let 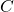 be a smooth projective curve over a finite field
be a smooth projective curve over a finite field 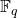 . Let
. Let 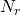 be the set of
be the set of 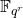 points of
points of 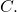 Then the zeta function of
Then the zeta function of 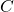 is defined by
is defined by
![Rendered by QuickLaTeX.com \[Z(C, T) = \exp \bigg(\sum_{r=1}^{\infty} N_r \frac{T^r}{r} \bigg).\]](https://www.ocf.berkeley.edu/~rohanjoshi/wp-content/ql-cache/quicklatex.com-cd792f705a3532be2b05801adabb9e80_l3.png)
Here, we are using 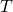 as a change of variables: if we plug in
as a change of variables: if we plug in 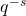 for
for 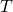 , then we obtain an exactly analogous zeta function to the Riemann zeta function, except with respect to the function field of
, then we obtain an exactly analogous zeta function to the Riemann zeta function, except with respect to the function field of 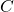 instead of the field
instead of the field  . There are three important properties that we would like
. There are three important properties that we would like 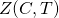 to have: (1) rationality, (2) satisfies a functional equation, and (3) satisfies an analogue of the Riemann hypothesis. Part (3) was proved by André Weil in the 1940’s; parts (1) and (2) were proved much earlier. In this post, I will present a proof of the analogue of the Riemann hypothesis assuming (1) and (2), along the lines of Weil’s original proof using intersection theory. All this material and much more is in an expository paper by James Milne called “The Riemann Hypothesis over Finite Fields: From Weil to the Present Day”. A useful reference is Appendix C in Hartshorne’s Algebraic Geometry; some material also comes from section V.1 on surfaces.
to have: (1) rationality, (2) satisfies a functional equation, and (3) satisfies an analogue of the Riemann hypothesis. Part (3) was proved by André Weil in the 1940’s; parts (1) and (2) were proved much earlier. In this post, I will present a proof of the analogue of the Riemann hypothesis assuming (1) and (2), along the lines of Weil’s original proof using intersection theory. All this material and much more is in an expository paper by James Milne called “The Riemann Hypothesis over Finite Fields: From Weil to the Present Day”. A useful reference is Appendix C in Hartshorne’s Algebraic Geometry; some material also comes from section V.1 on surfaces.
Let 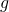 be the genus of
be the genus of 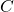 . Then (1) says that
. Then (1) says that 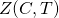 is a rational function of
is a rational function of 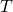 . The specific function equation of (2) is the following:
. The specific function equation of (2) is the following:
![Rendered by QuickLaTeX.com \[Z(C, \frac{1}{qT}) = q^{1-g}T^{2-2g} Z(C, T)\]](https://www.ocf.berkeley.edu/~rohanjoshi/wp-content/ql-cache/quicklatex.com-4e675f763db96169cf6387e4907ffed2_l3.png)
It turns out that we can write out 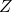 explicitly: there exist constants
explicitly: there exist constants 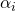 for
for 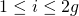 such that
such that
![Rendered by QuickLaTeX.com \[Z(C, T) = \frac{(1- \alpha_1T) \cdots (1 - \alpha_{2g}T)}{(1-T)(1-qT)}\]](https://www.ocf.berkeley.edu/~rohanjoshi/wp-content/ql-cache/quicklatex.com-7d8f90b25caa82eb74e24af89a42f66c_l3.png)
and the functional equation implies that the constants 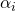 can be rearranged if necessary so that
can be rearranged if necessary so that
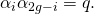
Now, the analogue of the Riemann hypothesis states the following:
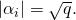
(To see the connection between this statement and the ordinary Riemann hypothesis, check out this blog post by Anton Hilado)
Notice that, assuming rationality and the functional equation, the Riemann hypothesis will follow from simply the inequality 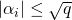 .
.
We will prove the Riemann hypothesis via the Hasse-Weil inequality, which is an inequality that puts an explicit bound on 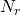 . The Hasse-Weil inequality states that
. The Hasse-Weil inequality states that
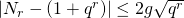
which is actually a pretty good bound. Why does the Hasse-Weil inequality imply the Riemann hypothesis? Well, if we take the logarithm of 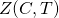 and use the power series for
and use the power series for 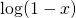 , regrouping terms gives us
, regrouping terms gives us
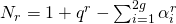 ; so
; so 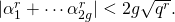
In other words,
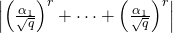 is bounded.
is bounded.
Letting 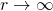 , we have
, we have
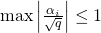 , so
, so 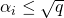 for all
for all 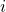
as desired. (check this works, even if 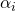 are not distinct)
are not distinct)
Proof of the Hasse-Weil inequality
We will prove the Hasse-Weil inequality using intersection theory. First, we will consider 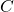 as a curve over
as a curve over 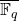 . Then there is the Frobenius map
. Then there is the Frobenius map 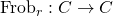 . If we embed
. If we embed 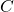 into projective space, then
into projective space, then 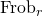 sends
sends ![Rendered by QuickLaTeX.com [x_0 : \cdots : x_n] \mapsto [x_0^{q_r} : \cdots : x_n^{q^r}]](https://www.ocf.berkeley.edu/~rohanjoshi/wp-content/ql-cache/quicklatex.com-38e48e49691612d94147383afe65e570_l3.png) . We can interpret
. We can interpret 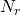 as the size of the set of fixed points of
as the size of the set of fixed points of 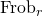 . Our plan then to use inequalities from intersection theory to bound the intersection of
. Our plan then to use inequalities from intersection theory to bound the intersection of 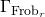 and
and 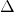 (the diagonal) in
(the diagonal) in 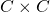 .
.
First, let us set up the intersection theory we need. This material is from Chapter V.1 of Hartshorne, on surfaces.
Intersection pairing on a surface: Let 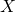 be a surface. There exists a symmetric bilinear pairing
be a surface. There exists a symmetric bilinear pairing 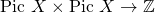 (where the product of divisors
(where the product of divisors 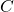 and
and 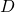 is denoted
is denoted 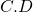 ) such that if
) such that if 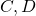 are smooth curves intersecting transversely, then
are smooth curves intersecting transversely, then
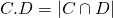 .
.
Furthermore, another theorem we’ll need is the Hodge index theorem:
Let 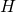 be an ample divisor on
be an ample divisor on 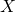 and
and 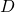 a nonzero divisor, with
a nonzero divisor, with 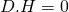 . Then
. Then 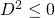 . (
. (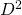 denotes
denotes 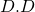 )
)
Now let us begin with some general set up. Let 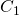 and
and 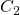 be two curves, and let
be two curves, and let 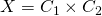 . Identify
. Identify 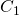 with
with 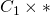 and
and 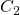 with
with 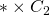 . Notice that
. Notice that 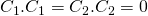 and
and 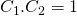 . Thus
. Thus 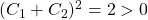 .
.
Let 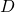 be a divisor on
be a divisor on 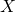 . Let
. Let 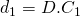 and
and 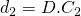 ; also,
; also, 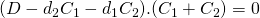 (expand it out). The Hodge index theorem implies then that
(expand it out). The Hodge index theorem implies then that 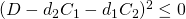 . Expanding this out yields
. Expanding this out yields 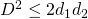 . This fundamental inequality is called the Castelnuovo-Severi inequality. We may define
. This fundamental inequality is called the Castelnuovo-Severi inequality. We may define 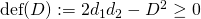 .
.
Next, let us prove the following inequality: if 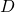 and
and 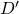 are divisors, then
are divisors, then
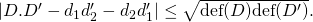
Proof (fill in details): Expand out 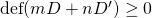 , for
, for 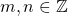 . We can let
. We can let 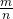 become arbitrarily close to
become arbitrarily close to  , yielding the inequality.
, yielding the inequality. 
Here’s another lemma we will need: Consider a map 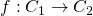 . If
. If 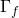 is the graph of
is the graph of 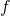 on
on 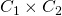 , then
, then 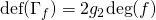 (where
(where 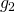 is the genus of
is the genus of 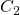 ).
).
Proof (fill in details): Rearrange adjunction formula. 
Now we have what we need: we will do intersection theory on 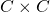 . The Frobenius map
. The Frobenius map 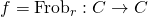 is a map of degree
is a map of degree 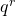 , so
, so 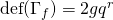 . We might as well think of
. We might as well think of 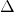 as the graph of the identity map, so
as the graph of the identity map, so 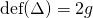 . Finally,
. Finally, 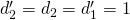 and
and 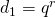 . Plugging it into the inequality, we get
. Plugging it into the inequality, we get
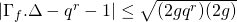
yielding the Hasse-Weil inequality
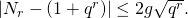
This proves the Riemann hypothesis for function fields, or equivalently the Riemann hypothesis curves over finite fields.
The Weil conjectures
After Weil proved this result, he speculated whether analogous statements were true for not only curves over finite fields, but higher-dimensional algebraic varieties over finite fields. He proposed as conjectures that the zeta functions for such varieties should also satisfy (1) rationality, (2) a functional equation, and (3) an analogoue of the Riemann hypothesis.
Weil also speculated a connection with algebraic topology. In our work above, the genus 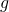 was crucial. But the genus can alternatively be defined topologically, by taking the equations that define the curve, looking at the locus they cut out when graphed over the complex numbers, and counting how many holes the resulting shape has. Weil suggested that for arbitrary varieties, topological Betti numbers should play this role: that is, the zeta function of the variety over the finite field should be closely connected with the topology of the analogous variety over the complex numbers.
was crucial. But the genus can alternatively be defined topologically, by taking the equations that define the curve, looking at the locus they cut out when graphed over the complex numbers, and counting how many holes the resulting shape has. Weil suggested that for arbitrary varieties, topological Betti numbers should play this role: that is, the zeta function of the variety over the finite field should be closely connected with the topology of the analogous variety over the complex numbers.
There’s an interesting blog post that discusses this idea, in our context of curves. But the rest is history. The story of the Weil conjectures is one of the most famous in all of mathematics: the effort to prove them revolutionized algebraic geometry and number theory forever. The key innovation was the theory of étale cohomology, which is an analogue of classical singular cohomology for algebraic varieties over arbitrary fields.
![]() is a cover of a topological space
is a cover of a topological space ![]() . What does it take to glue continuous functions
. What does it take to glue continuous functions ![]() on
on ![]() into a function on all of
into a function on all of ![]() ?
?![]() for all pairs
for all pairs ![]() , then they glue uniquely to a function
, then they glue uniquely to a function ![]() on
on ![]() such that
such that ![]() .
.![]() be the disjoint union of the
be the disjoint union of the ![]() s. Then we have a surjective “cover”
s. Then we have a surjective “cover” ![]() . Combine the
. Combine the ![]() s into a function on
s into a function on ![]() called
called ![]() . Then what we are trying to do is see if the function
. Then what we are trying to do is see if the function ![]() on
on ![]() can be “descended” to
can be “descended” to ![]() i.e. we are trying to find functions
i.e. we are trying to find functions ![]() on
on ![]() , if any, such that when such a function is pulled back to
, if any, such that when such a function is pulled back to ![]() it is
it is ![]() . Note here that by “is” we mean the functions are literally identical. We can also reformulate what is means for the
. Note here that by “is” we mean the functions are literally identical. We can also reformulate what is means for the ![]() s to agree on intersections. The fiber product of
s to agree on intersections. The fiber product of ![]() with itself over
with itself over ![]() has two maps, left and right projection, down to
has two maps, left and right projection, down to ![]() :
:![]()
![]() and
and ![]() . Then for the
. Then for the ![]() to “agree on intersections” is equivalent to the statement
to “agree on intersections” is equivalent to the statement ![]() as functions on
as functions on ![]() (think about this!). We’ll return to this later. Now, let’s step up one level, from functions to vector bundles.
(think about this!). We’ll return to this later. Now, let’s step up one level, from functions to vector bundles.![]() is a cover of a topological space
is a cover of a topological space ![]() . What does it take to glue vector bundles (or sheaves)
. What does it take to glue vector bundles (or sheaves) ![]() to a vector bundle
to a vector bundle ![]() ? We also know the answer to this: transition maps satisfying the cocyle condition. More precisely, we need for each pair
? We also know the answer to this: transition maps satisfying the cocyle condition. More precisely, we need for each pair ![]() an isomorphism of vector bundles
an isomorphism of vector bundles ![]() restricted to
restricted to ![]() , such that for every triple
, such that for every triple ![]() ,
, ![]() on the triple intersection
on the triple intersection ![]() .
.![]() s again. Let’s call
s again. Let’s call ![]() the disjoint union of the
the disjoint union of the ![]() and combine the
and combine the ![]() together as a single vector bundle
together as a single vector bundle ![]() . What we’re trying to do is “descend” this vector bundle over
. What we’re trying to do is “descend” this vector bundle over ![]() to
to ![]() .
.![]() . It has three projections down to
. It has three projections down to ![]() (by omitting any of the three factors).
(by omitting any of the three factors).![]()
![]() .
. ![]() of vector bundles, and the cocycle condition translates to
of vector bundles, and the cocycle condition translates to ![]()
![]() which assigns to every base object the set of (insert adjective) functions on it. Then such a functor (presheaf) is a sheaf if, for every function on
which assigns to every base object the set of (insert adjective) functions on it. Then such a functor (presheaf) is a sheaf if, for every function on ![]() which, along the two projections
which, along the two projections ![]() , is pulled to identical functions, is the unique pullback of a function on
, is pulled to identical functions, is the unique pullback of a function on ![]() . In other words
. In other words ![]() is the equalizer
is the equalizer ![]() .
.![]() is: an element of
is: an element of ![]() , and a truth value on
, and a truth value on ![]() (the truth value is whether the “functions” agree).
(the truth value is whether the “functions” agree).![]() which assigns to every base object the category of sheaves over it. Then such a functor is a 2-sheaf if for every sheaf on
which assigns to every base object the category of sheaves over it. Then such a functor is a 2-sheaf if for every sheaf on ![]() , there is an isomorphism between the pullbacks along the two projections
, there is an isomorphism between the pullbacks along the two projections ![]() , and these isomorphisms, pulled back to
, and these isomorphisms, pulled back to ![]() (along the three projections
(along the three projections ![]() ), satisfy a cocyle condition. If such a thing made sense, we might say
), satisfy a cocyle condition. If such a thing made sense, we might say ![]() is equivalent, as a category, to the following “2-limit of categories”:
is equivalent, as a category, to the following “2-limit of categories”:![]()
![]() is: an object of
is: an object of ![]() , isomorphism of
, isomorphism of ![]() , and truth value on
, and truth value on ![]() . Each morphism of
. Each morphism of ![]() is: morphism of
is: morphism of ![]() , truth value on
, truth value on ![]() . (morphism of descent datum)
. (morphism of descent datum)![]() which assigns to every base object the 2-category of sheaves of 1-categories over it.
which assigns to every base object the 2-category of sheaves of 1-categories over it. ![]() is: an object of
is: an object of ![]() , isomorphism of
, isomorphism of ![]() , 2-isomorphism of
, 2-isomorphism of ![]() , and a truth value on
, and a truth value on ![]() . A morphism of
. A morphism of ![]() is a morphism of
is a morphism of ![]() , a 2-morphism of
, a 2-morphism of ![]() , and a truth value in
, and a truth value in ![]() . A 2-morphism of
. A 2-morphism of ![]() is a 2-morphism in
is a 2-morphism in ![]() and a truth value on
and a truth value on ![]() .
.![Rendered by QuickLaTeX.com \[Z(C, T) = \exp \bigg(\sum_{r=1}^{\infty} N_r \frac{T^r}{r} \bigg).\]](https://www.ocf.berkeley.edu/~rohanjoshi/wp-content/ql-cache/quicklatex.com-cd792f705a3532be2b05801adabb9e80_l3.png)
![Rendered by QuickLaTeX.com \xymatrix{R\ar[r]^{\phi}\ar[d]^{\phi} & {R[t^\pm]} \ar[d]^{id_R\otimes \mu}\\{R[u^\pm]} \ar[r]^{\phi \otimes id_{k[u^\pm]}} & {R[t^\pm, u^\pm]}}](https://www.ocf.berkeley.edu/~rohanjoshi/wp-content/ql-cache/quicklatex.com-be58b01614e66fda49f67e15ebbc62ce_l3.png)
![Rendered by QuickLaTeX.com \xymatrix{R\ar[r]^{\phi}\ar[d]^{id_R} & {R[t^\pm]} \ar[dl]^{i}\\ R}](https://www.ocf.berkeley.edu/~rohanjoshi/wp-content/ql-cache/quicklatex.com-328480c25d8ee63a186221bdc075521c_l3.png)