A complex number is algebraic if it is the root of some polynomial 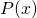 with rational coefficients.
with rational coefficients. 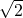 is algebraic (e.g. the polynomial
is algebraic (e.g. the polynomial 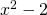 );
); 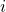 is algebraic (e.g. the polynomial
is algebraic (e.g. the polynomial 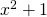 );
); 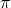 and
and  are not. A complex number that is not algebraic is called transcendental.
are not. A complex number that is not algebraic is called transcendental.
Is the sum of algebraic numbers always algebraic? What about the product of algebraic numbers? For example, given that 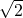 and
and 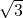 are algebraic, how do we know
are algebraic, how do we know 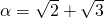 is also algebraic?
is also algebraic?
We can try to repeatedly square the equation 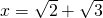 . This gives us
. This gives us 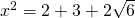 . Then isolating the radical, we have
. Then isolating the radical, we have 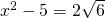 . Squaring again, we get
. Squaring again, we get 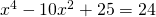 , so
, so 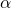 is a root of
is a root of 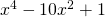 . This is in fact the unique monic polynomial of minimum degree that has
. This is in fact the unique monic polynomial of minimum degree that has 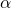 as a root (called the minimal polynomial of
as a root (called the minimal polynomial of 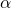 ) which shows
) which shows 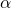 is algebraic. But a sum like
is algebraic. But a sum like 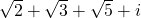 would probably have a minimal polynomial of much greater degree, and it would be much more complicated to construct this polynomial and verify the number is algebraic.
would probably have a minimal polynomial of much greater degree, and it would be much more complicated to construct this polynomial and verify the number is algebraic.
It is also increasingly difficult to construct polynomials for numbers like ![Rendered by QuickLaTeX.com \sqrt{2} + \sqrt[3]{3}](https://www.ocf.berkeley.edu/~rohanjoshi/wp-content/ql-cache/quicklatex.com-677de06a24a7c6f091d4ecd95aa1f71f_l3.png) . And, apparently there also exist algebraic numbers that cannot be expressed as radicals at all. This further complicates the problem.
. And, apparently there also exist algebraic numbers that cannot be expressed as radicals at all. This further complicates the problem.
In fact, the sum and product of algebraic numbers is algebraic – in fact, any number which can be obtained by adding, subtracting, multiplying and dividing algebraic numbers is algebraic. This means that a number like
![Rendered by QuickLaTeX.com \[\frac{\sqrt{2} + i\sqrt[3]{25} - 2 + \sqrt{3}}{15 - 3i + 4e^{5i\pi / 12}}\]](https://www.ocf.berkeley.edu/~rohanjoshi/wp-content/ql-cache/quicklatex.com-c53353269b5c7eb7cd6f8ad37a107c3b_l3.png)
is algebraic – there is some polynomial which has it as a root. But we will prove this result non-constructively; that is, we will prove that such a number must be algebraic, without providing an explicit process to actually obtain the polynomial. To establish this result, we will try to look for a deeper structure in the algebraic numbers, which is elucidated, perhaps surprisingly, using the tools of linear algebra.
Definition: Let 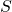 be a set of complex numbers that contains
be a set of complex numbers that contains 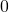 . We say
. We say 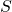 is an abelian group if for all
is an abelian group if for all 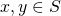 ,
, 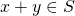 and
and 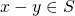 . In other words,
. In other words, 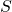 is closed under addition and subtraction.
is closed under addition and subtraction.
Some examples: 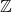 ,
, 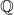 ,
, 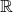 ,
, 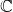 , the Gaussian integers
, the Gaussian integers ![Rendered by QuickLaTeX.com \mathbb{Z}[i]](https://www.ocf.berkeley.edu/~rohanjoshi/wp-content/ql-cache/quicklatex.com-4ebd227e9a6e5ac81369a7b6d868695b_l3.png) (i.e. the set of expressions
(i.e. the set of expressions 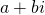 where
where  and
and 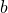 are integers)
are integers)
Definition: An abelian group is a field if it contains 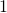 and for all
and for all 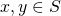 ,
, 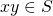 , and if
, and if 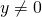 ,
, 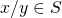 . In other words,
. In other words, 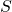 is closed under multiplication and division.
is closed under multiplication and division.
We generally use the letters  ,
, 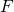 ,
, 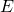 for arbitrary fields. Of the previous examples, only
for arbitrary fields. Of the previous examples, only 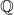 ,
, 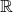 ,
, 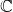 are fields.
are fields.
Exercise: Show that if  is a field,
is a field, 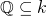 .
.
Exercise: Show that the set 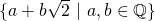 is a field. We call this field
is a field. We call this field 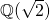 . (Hint: rationalize the denominator).
. (Hint: rationalize the denominator).
Exercise: Describe the the smallest field which contains both 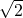 and
and 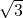 (this is called
(this is called 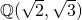 )
)
Generally if  is a field and
is a field and 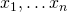 some complex numbers, we will denote the smallest field that contains all of
some complex numbers, we will denote the smallest field that contains all of  and the elements
and the elements 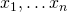 as
as 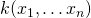 .
.
Definition: Let  be a field. A
be a field. A  -vector space is an abelian group
-vector space is an abelian group 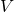 such that if
such that if 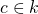 ,
, 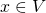 , then
, then 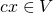 . Intuitively, the elements of
. Intuitively, the elements of 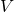 are closed under scaling by
are closed under scaling by  . (We also sometimes use the phrase “
. (We also sometimes use the phrase “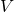 is a vector space over
is a vector space over  “)
“)
Examples: 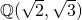 and
and 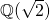 are both
are both 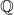 -vector spaces. In fact,
-vector spaces. In fact, 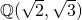 is also a
is also a 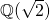 vector space.
vector space.
With this language in place, we can state the main goal of this post as follows:
Theorem: If 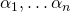 are algebraic numbers and
are algebraic numbers and 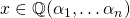 , then
, then 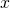 is algebraic.
is algebraic.
Note how this encompasses our previous claim that any number obtained by adding, subtracting, multiplying and dividing algebraic numbers is algebraic. For example, we can deduce the giant fraction above is algebraic by applying the theorem to ![Rendered by QuickLaTeX.com \mathbb{Q}(\sqrt{2}, i, \sqrt[3]{25}, \sqrt{3}, e^{5i/12})](https://www.ocf.berkeley.edu/~rohanjoshi/wp-content/ql-cache/quicklatex.com-468ee35a1342cfe2783536815a0448e4_l3.png) .
.
Definition: A field extension of a field  is just a field
is just a field 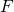 that contains
that contains  . We will write this as “
. We will write this as “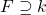 is a field extension”.
is a field extension”.
Exercise: If 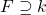 is a field extension, then
is a field extension, then 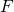 is a
is a  -vector space
-vector space
Consider a field like 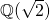 . Not only is it a field, but it is also a
. Not only is it a field, but it is also a 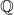 -vector space – its elements can be scaled by rational numbers. We want to adapt concepts from ordinary linear algebra to this setting. We want to think of
-vector space – its elements can be scaled by rational numbers. We want to adapt concepts from ordinary linear algebra to this setting. We want to think of 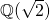 as a two dimensional vector space, with basis
as a two dimensional vector space, with basis 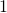 and
and 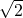 – every element is can be uniquely written as a
– every element is can be uniquely written as a  -linear combination of
-linear combination of 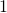 and
and 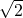 . Similarly, we would like to think of
. Similarly, we would like to think of 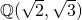 as a
as a  -vector space with basis
-vector space with basis 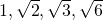 . Note that if we regard
. Note that if we regard 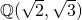 as a
as a 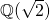 -vector space, its basis is
-vector space, its basis is 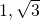 . This is because if an element is written as
. This is because if an element is written as 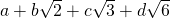 , where the coefficients are rational, we can rewrite it as
, where the coefficients are rational, we can rewrite it as 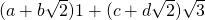 , now with coefficients in
, now with coefficients in 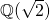 .
.
On the other hand, consider 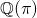 . Since
. Since 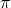 is not algebraic, no linear combination (with rational coefficients) of the numbers
is not algebraic, no linear combination (with rational coefficients) of the numbers 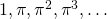 equals
equals 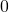 without all the coefficients being zero. This makes them linearly independent – and makes
without all the coefficients being zero. This makes them linearly independent – and makes 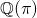 an infinite-dimensional vector space.
an infinite-dimensional vector space.
This finite-versus-infinite dimensionality difference will lie at the crux of our argument. Here is a rough summary of the argument to prove the Theorem:
- If we add an algebraic number to a field, we get a finite-dimensional vector space over that field.
- By repeatedly adding algebraic numbers to
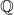 , the resulting field will still be a finite-dimensional
, the resulting field will still be a finite-dimensional 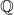 -vector space.
-vector space. - Any element of a field which is a finite-dimensional
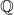 -vector space must be algebraic.
-vector space must be algebraic.
From here on, we will assume that the reader has some familiarity with ideas from linear algebra, such as the notions of linear combination, linear independence, and basis. We will only sketch proofs (maybe I will add details later). We would like to warn the reader that the proof sketches have many gaps and may be difficult to follow.
Definition: A field extension 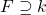 is finite if there is a finite set of elements
is finite if there is a finite set of elements 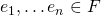 such that every element of
such that every element of 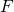 can be represented as
can be represented as 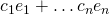 , where all the
, where all the 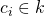 . We say the elements
. We say the elements 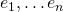 generate (aka span)
generate (aka span) 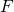 over
over  . If, furthermore, every element can be represented uniquely in this form, then we say
. If, furthermore, every element can be represented uniquely in this form, then we say 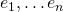 is a
is a  –basis (or just basis) for
–basis (or just basis) for 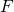 .
.
Examples: 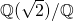 and
and 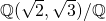 are finite extensions, while
are finite extensions, while 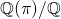 is not.
is not.
Exercise: Show 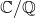 is not a finite extension. (Hint:
is not a finite extension. (Hint: 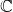 is uncountable)
is uncountable)
Proposition 1: Every finite field extension 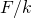 has a basis.
has a basis.
Proof sketch: This is a special case of a famous theorem in linear algebra. Assume 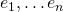 generate
generate 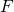 . Start with the last element. If
. Start with the last element. If 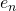 can be represented as a linear combination of
can be represented as a linear combination of 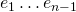 , remove it from the list. If we removed
, remove it from the list. If we removed 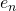 , we now have
, we now have 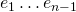 , and we can repeat the process with
, and we can repeat the process with 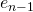 . Continue this process until we cannot remove any more elements. Then (it can be checked that) we obtain a set whose elements are linearly independent. Then (it can be checked that) these form a
. Continue this process until we cannot remove any more elements. Then (it can be checked that) we obtain a set whose elements are linearly independent. Then (it can be checked that) these form a  -basis for
-basis for 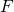 .
. 
For the next theorem, keep in mind the example of the extensions 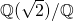 and
and 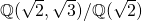 .
.
Proposition 2: Suppose 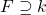 and
and 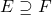 are finite field extensions. Then
are finite field extensions. Then 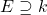 is a finite extension.
is a finite extension.
Proof: By Proposition 1, both these field extensions have bases. Label the 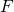 -basis of
-basis of 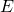 as
as 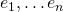 , and the
, and the  -basis for
-basis for 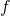 as
as  . Then every element of
. Then every element of 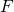 can be uniquely represented as
can be uniquely represented as 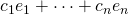 , for
, for 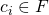 . Furthermore, each
. Furthermore, each 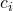 can be written uniquely as
can be written uniquely as 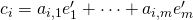 for
for 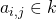 . Plugging these in for the
. Plugging these in for the 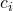 shows that the
shows that the 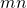 elements of the form
elements of the form 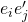 form a
form a  -basis for
-basis for 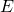 .
. 
Proposition 3: If 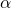 is algebraic, then
is algebraic, then 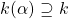 is a finite extension.
is a finite extension.
Proof sketch: Suppose 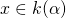 . First we will show every element in
. First we will show every element in 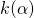 is a polynomial in
is a polynomial in 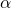 with coefficients in
with coefficients in  .
. 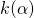 consists of all numbers that can be obtained by repeatedly adding, subtracting, multiplying and dividing
consists of all numbers that can be obtained by repeatedly adding, subtracting, multiplying and dividing 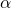 and elements of
and elements of  . By performing some algebraic manipulations and combining fractions, we can see that every element can be written in the form
. By performing some algebraic manipulations and combining fractions, we can see that every element can be written in the form 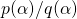 , where
, where 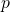 and
and 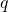 are polynomials with coefficients in
are polynomials with coefficients in  .
.
Now I claim that for any polynomial 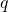 where
where 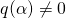 , there exists a polynomial
, there exists a polynomial  such that
such that 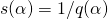 . Let
. Let 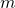 be the minimal polynomial of
be the minimal polynomial of 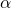 . Since
. Since 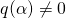 and
and 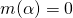 ,
, 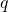 and
and 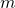 are relatively prime as polynomials. So there exist polynomials
are relatively prime as polynomials. So there exist polynomials  and
and  such that
such that 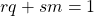 . Plugging in
. Plugging in 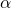 into the polynomials gives us
into the polynomials gives us 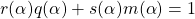 . Since
. Since 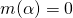 ,
, 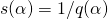 , as desired.
, as desired.
Thus any element in 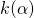 , written as
, written as 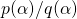 , can be written as
, can be written as 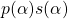 for an appropriate polynomial
for an appropriate polynomial  ; in other words, every element of
; in other words, every element of 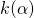 is a polynomial of
is a polynomial of 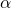 with coefficients in
with coefficients in  . Now, suppose the minimal polynomial of
. Now, suppose the minimal polynomial of 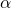 is
is 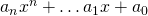 . Then
. Then 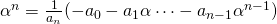 . So
. So 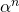 (and all higher powers of
(and all higher powers of 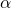 ) can be written as rational linear combinations of
) can be written as rational linear combinations of 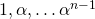 . Then it can be verified that every element in
. Then it can be verified that every element in 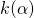 can be written uniquely as a
can be written uniquely as a  -linear combination of
-linear combination of 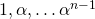 . This establishes that
. This establishes that 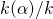 is a finite extension; in particular, it has the basis
is a finite extension; in particular, it has the basis 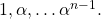

Proposition 4: Suppose 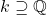 is a finite extension. Then any
is a finite extension. Then any 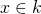 is algebraic.
is algebraic.
Proof sketch: Consider the elements 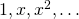 . They cannot all be linearly independent. This is because in a finite-dimensional vector space of dimension
. They cannot all be linearly independent. This is because in a finite-dimensional vector space of dimension 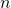 any set with at least
any set with at least 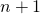 elements must be linearly dependent. So there must be some linear combination of them which equals zero. But this simply means that for some constants
elements must be linearly dependent. So there must be some linear combination of them which equals zero. But this simply means that for some constants 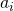 and positive integer
and positive integer 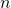 ,
, 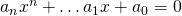 . Letting the
. Letting the 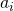 be the coefficients of a polynomial
be the coefficients of a polynomial 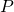 ,
, 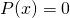 , so
, so 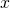 is algebraic.
is algebraic. 
We have developed enough theory now to prove the result.
Proof of main Theorem: Let 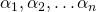 be some collection of algebraic numbers. Then by Proposition 3,
be some collection of algebraic numbers. Then by Proposition 3, 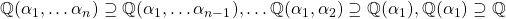 are all finite field extensions. Applying Proposition 2 repeatedly gives us
are all finite field extensions. Applying Proposition 2 repeatedly gives us 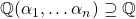 is a finite extension. Then by Proposition 4, any element of
is a finite extension. Then by Proposition 4, any element of 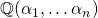 is algebraic.
is algebraic.
This theorem essentially says that given a collection of algebraic numbers, by repeatedly adding, subtracting, multiplying and dividing them, we can only obtain algebraic numbers. But what about radicals? For example, we have now established that 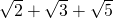 is algebraic. Is
is algebraic. Is 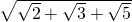 algebraic as well?
algebraic as well?
In fact, we can generalize our result to the following: any number obtained by repeatedly adding, subtracting, multiplying, dividing algebraic numbers, as well as taking 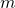 -th roots (for positive integers
-th roots (for positive integers 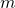 ) will be algebraic.
) will be algebraic.
This is not too hard now that we have the main theorem. It suffices to show that if 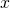 is algebraic,
is algebraic, ![Rendered by QuickLaTeX.com \sqrt[m]{x}](https://www.ocf.berkeley.edu/~rohanjoshi/wp-content/ql-cache/quicklatex.com-60272e5d6d6207814e6d7ee4c2bf6c8f_l3.png) is algebraic. If
is algebraic. If 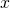 is algebraic, then there exist constants
is algebraic, then there exist constants 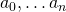 such that
such that 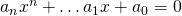 . This can be rewritten as
. This can be rewritten as ![Rendered by QuickLaTeX.com a_n(\sqrt[m]{x})^{mn} + \dots a_1(\sqrt[m]{x})^m + a_0 = 0](https://www.ocf.berkeley.edu/~rohanjoshi/wp-content/ql-cache/quicklatex.com-f7a59cd1e27d04dfdb1a565411131be8_l3.png) . Thus
. Thus ![Rendered by QuickLaTeX.com \sqrt[m]{x}](https://www.ocf.berkeley.edu/~rohanjoshi/wp-content/ql-cache/quicklatex.com-60272e5d6d6207814e6d7ee4c2bf6c8f_l3.png) is algebraic.
is algebraic.
Acknowledgements: Thanks to Anton Cao and Nagaganesh Jaladanki for reviewing this article.
![]() over the complex numbers (or more generally, over an algebraically closed field) has an eigenvalue. Notice that this is equivalent to finding a complex number
over the complex numbers (or more generally, over an algebraically closed field) has an eigenvalue. Notice that this is equivalent to finding a complex number ![]() such that
such that ![]() has nontrivial kernel. The first proof uses facts about “linear dependence” and the second uses determinants and the characteristic polynomial. The first proof is drawn from Axler’s textbook [1]; the second is the standard proof.
has nontrivial kernel. The first proof uses facts about “linear dependence” and the second uses determinants and the characteristic polynomial. The first proof is drawn from Axler’s textbook [1]; the second is the standard proof.![]() be a polynomial with complex coefficients. If
be a polynomial with complex coefficients. If ![]() is a linear map,
is a linear map, ![]() . We think of this as “
. We think of this as “![]() evaluated at
evaluated at ![]() ”.
”.![]() .
.![]() . Consider the sequence of vectors
. Consider the sequence of vectors ![]() This is a set of
This is a set of ![]() vectors, so they must be linearly dependent. Thus there exist constants
vectors, so they must be linearly dependent. Thus there exist constants ![]() such that
such that ![]()
![]() .
. ![]() . Then, we can factor
. Then, we can factor ![]() By the Exercise, this implies
By the Exercise, this implies ![]() . So, at least one of the maps
. So, at least one of the maps ![]() has a nontrivial kernel, so
has a nontrivial kernel, so ![]() has an eigenvalue.
has an eigenvalue. ![]()
![]() such that
such that ![]() has nontrivial kernel: in other words, that
has nontrivial kernel: in other words, that ![]() is singular. A matrix is singular if and only if its determinant is nonzero. So, let
is singular. A matrix is singular if and only if its determinant is nonzero. So, let ![]() ; this is a polynomial in
; this is a polynomial in ![]() , called the characteristic polynomial of
, called the characteristic polynomial of ![]() . Now, every polynomial has a complex root, say
. Now, every polynomial has a complex root, say ![]() . This implies
. This implies ![]() , so
, so ![]() has an eigenvalue.
has an eigenvalue. ![]()
![Rendered by QuickLaTeX.com \xymatrix{R\ar[r]^{\phi}\ar[d]^{\phi} & {R[t^\pm]} \ar[d]^{id_R\otimes \mu}\\{R[u^\pm]} \ar[r]^{\phi \otimes id_{k[u^\pm]}} & {R[t^\pm, u^\pm]}}](https://www.ocf.berkeley.edu/~rohanjoshi/wp-content/ql-cache/quicklatex.com-be58b01614e66fda49f67e15ebbc62ce_l3.png)
![Rendered by QuickLaTeX.com \xymatrix{R\ar[r]^{\phi}\ar[d]^{id_R} & {R[t^\pm]} \ar[dl]^{i}\\ R}](https://www.ocf.berkeley.edu/~rohanjoshi/wp-content/ql-cache/quicklatex.com-328480c25d8ee63a186221bdc075521c_l3.png)