archimidean property | Arithmetic variety

In the previous post we discussed the Archimedean property for an ordered field. Today I’ll discuss the Archimedean property for valued fields, that is, fields equipped with an absolute value.

Recall that an absolute value on a field $K$ is a function $| \ |: K \to \mathbb{R}_{\geq 0}$ satisfying the following axioms:

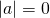$|a| = 0$ if and only if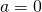 $a = 0$
$|ab| = |a||b|$
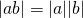
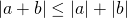$|a+b| \leq |a| + |b|$ (triangle inequality)

for all $a, b \in K$ .

Here is an intuitive, analogous definition for the Archimedean property:

Definition: The absolute value $| \ |$ is Archimedean if, for $x, y \in K$ , $x \neq 0$ , $|nx| > |y|$ for some natural number $n$ .

Clearly the standard absolute value (which is defined on $\mathbb{C}$ and $\mathbb{R}$ , and therefore $\mathbb{Q}$ ) is Archimedean. But wait: since we assumed $x \neq 0$ , we can divide both sides by $|x|$ to obtain $|n| > |y/x|$ . In other words, we can write the definition equivalently as:

Equivalent Definition: The absolute value $| \ |$ is Archimedean if, for all $a \in K$ , $|n| > |a|$ for some natural number $n$ .

Here $a$ takes the place of $y/x$ . The important thing here is that $a$ can be any element of $K.$ So what this is saying is that, given any element of the field, there is some natural number that beats it.

Now, let us assume that the absolute value is nontrivial. (The trivial absolute value has $|a| = 1$ for all nonzero $a$ ). Thus, for some $a$ , $|a| \neq 1$ . So, either $|a| > 1$ or $|1/a| = 1/|a| > 1$ . Thus by taking arbitrarily high powers of $a$ or $1/a$ , we can obtain arbitrarily high absolute values. So we can reformulate the definition as follows:

Equivalent Definition: $| \ |$ is Archimedean if the set $\{ |n| \ | \ n \in \mathbb{N}\}$ contains arbitrarily large elements.

In other words, the set is unbounded. So, $| \ |$ is non-Archimedean if the sequence $|1|, |2|, |3|, \dots$ is bounded. However, if any $|n| > 1$ , then taking arbitrarily high powers of $n$ can give us arbitrarily high absolute values. So

Equivalent Definition: $| \ |$ is non-Archimedean if $|n| \leq 1$ for $n \in \mathbb{N}$ .

Finally, I will present another very useful characterization of the (non)Archimedean property.

Theorem/Equivalent Definition: $| \ |$ is non-Archimedean if $|a+b| \leq \text{max}(|a|, |b|)$ .

Proof: (to be added)

If $a$ and $b$ are positive real numbers, if you add $a$ to itself enough times, eventually you will surpass $b$ . This is called the Archimedean property, and it is one of the fundamental properties of the system of real numbers. Informally, what this property says is that no numbers are infinitely larger than others. We can formally define this property as follows:

Let $F$ be an ordered field. We say $F$ is Archimedean if, for $x, y \in F$ where $x, y > 0$ , there exists a natural number $n$ such that $nx > y$ .

An example of a non-Archimedean number system is the hyperreal numbers. Hyperreal numbers are an enlargement of the real numbers that also contain “infinite” and “infinitesimal” quantities. The hyperreal numbers are used to give an alternative formulation of calculus in the subject of non-standard analysis, where instead of using limits, one computes with actual infinitesimals.

More familiar examples of non-Archimedean fields are function fields. For example, consider the field of rational functions (on $\mathbb{R}$ ), denoted $\mathbb{R}(x)$ . We can order rational functions by declaring that

$p > q$ if $p(x) > q(x)$ as $x \to \infty$

for any $p, q \in \mathbb{R}(x)$ . In other words, we order rational functions by looking at their asymptotic behavior. One can check that this satisfies the axioms, making $\mathbb{R}(X)$ an ordered field.

Exercise: Show that a rational function

$p(x) = \frac{f(x)}{g(x)} = \frac{a_nx^n + \cdots + a_1x + a_0}{b_mx^m + \cdots + b_1x + a_0}$

is positive with respect to the order (i.e. $p > 0$ ) if and only if $a_n/b_m > 0$ .

Now one can see that the field of rational functions is clearly not Archimedean. For example, if we consider $p(x) = 1/x$ , no matter how many times we add it to itself, it will never surpass $q(x) = 1$ : the function $np(x) = \frac{n}{x}$ is eventually surpassed by $q(x) = 1$ , no matter how great $n$ is.

Exercise: Define the degree of a rational function to be the degree of its numerator minus the degree of its denominator. For rational functions $p, q > 0$ , show there exists an integer $n$ such that $np > q$ if and only if degree $(p) \geq$ degree $(q)$ .

Thus the basic idea of the Archimedean property is at the core of asymptotic analysis. In defining big-O notation, we write $f(x) = O(g(x))$ if some multiple of $f$ surpasses $g$ as $x$ goes off to infinity.

In the next post, I will discuss the Archimedean property for valued fields (as opposed to ordered fields), and how this applies to number theory.

Arithmetic variety

Tag Archives: archimidean property

Archimedean absolute values

The Archimedean property