Author |
Topic: Triangles, missing area (Read 16169 times) |
|
tommy cha cha
Guest
|
// 11/7/2002 4:20PM IMAGE REPRINTED HERE BY SITE ADMIN FOR YOUR CONVENIENCE
Hint: these triangles are not only different in size... they also differ also in shape.
|
| « Last Edit: Nov 7th, 2002, 3:05pm by william wu » |
 IP Logged |
|
|
|
D. Spig
Guest
|
 |
Re: Triangles, missing area
« Reply #1 on: Jul 25th, 2002, 8:33pm » |
 Quote  Modify
 Remove
|
Here is an even bigger hint. They aren't triangles! They have four sides, not three.
If you want to confirm this, check the slopes of the blue triangle verse the red triangle:
Red slope: 2/5
Blue slope: 3/8
These aren't equivalent.
This is a "hard" question only because the question lies by saying they are triangles. Perhaps shape would be better.
|
|
IP Logged |
|
|
|
Magneeto
Guest
|
|
Re: Triangles, missing area
« Reply #2 on: Jul 26th, 2002, 1:37am » |
Quote Modify
Remove
|
This one had me questioning the laws of math and physics(not to mention my sanity). I even drew them on graph paper and cut them out and made them fit.
A: The second triangle is larger, but only slightly. It is about 1/10 to 2/10 of a block larger on one or both sides. If one assumes the first is 5 by 13, then the second would only have to be 5.15 by 13.15 in order to account for the extra block.
using:
1\2 b * h = .5 * 5 * 13 = 32.5
in order to get 1 extra block 33.5
.5 * 5.15 * 13.15 = 33.86.
Yes they differ in size, but no, they do not differ in shape. They are stated to be triangles, and so despite the pixelation I treated them like triangles. I ain't no math major but I don't know of any rule that says the slopes of the sub-triangles must match in order to be considered a triangle. That's weird though, you would think they would have to. But, I can think of many examples in which the sub-triangles wouldn't match.
Still, I didn't like this question. Normally, questions like this expect you to disregard any imperfections in the picture, but this one uses those imperfections to fool you. The key is realizing that it only takes a minor change the base and/or height to change the area by a whole block. 
|
|
IP Logged |
|
|
|
l. abulafia
Guest
|
|
Re: Triangles, missing area
« Reply #3 on: Jul 26th, 2002, 1:49am » |
Quote Modify
Remove
|
Yes, Magneeto, they differ in shape.
You may have gotten the problem to work on graph paper by altering b & h, but that is not how -this- puzzle pulled the feat off. Here, base and height are the two sides that -are- symmetrical.
It's not quite accurate to say they have four sides, either, though on a low-resolution monitor it may appear there are.
If you wish to solve -this- problem, reconsider tommy cha cha's original advice.
Or, consider these (spoiling) terms: xevnoc and evacnoc.
|
|
IP Logged |
|
|
|
Mahender Akula
Guest
|
|
Re: Triangles, missing area
« Reply #4 on: Jul 26th, 2002, 8:45am » |
Quote Modify
Remove
|
The Blue and red square area are equal, because of dimensions.
I considered yellow and green as single entitiy (as rectangle)
So in the top picture the area comes out to be 3 x 5 = 15
In the bottom picture the area comes out to be 2 x 8 = 16
which includes the blank square. If you take blank square out
then it is 15.
Not sure if this is the solution.
Mahender
|
|
IP Logged |
|
|
|
hakaizou
Guest
|
|
Re: Triangles, missing area
« Reply #5 on: Jul 26th, 2002, 1:11pm » |
Quote Modify
Remove
|
D. Spig was right the first time: the shapes are NOT triangles to begin with, since the slopes of the hypotenuses of the blue and red triangles DON'T MATCH. It's an optical illusion, guys: a four-sided figure is made to look three sided.
Magneeto, the change is neither in the base nor the height, it's in the supposed "hypotenuse." See l. abulafia's hint. The figures were laid out on the grid to show that neither the "base" nor the "height" changed.
|
|
IP Logged |
|
|
|
Vineet Kumar
Guest
|
|
Re: Triangles, missing area
« Reply #6 on: Jul 26th, 2002, 1:47pm » |
Quote Modify
Remove
|
Yes, they do have 4 sides each. They are not triangles. The question lies.
Math major or no, surely you can see that a line with 2 different slopes is not a line. If you start out in one direction, and end up in another direction, somewhere in between, there's a point where you turned. That point is the vertex between the 2 edges, and it's folly to consider it one big edge, no matter how small (but nonzero) the angle between them is. There is a vertex on what is given as the hypotenuse of each of the large "triangles". Consider the extreme case: the opposite vertex. Surely you wouldn't consider the bottom side and the right side to be the same side -- there's a vertex there joining 2 edges with different slopes. If they had the same slope, they'd be the same side (and there'd be no vertex).
|
|
IP Logged |
|
|
|
S Spigarelli
Guest
|
|
Re: Triangles, missing area
« Reply #7 on: Jul 26th, 2002, 3:32pm » |
Quote Modify
Remove
|
Sounds like D. Spig is right. The riddle is a big lie. It confused me until I realized that it was a lie, not a really fair riddle.
|
|
IP Logged |
|
|
|
william wu
wu::riddles Administrator
Gender: 
Posts: 1291
|
|
Re: Triangles, missing area
« Reply #8 on: Jul 29th, 2002, 7:50pm » |
Quote Modify
|
"Believe nothing, no matter where you read it, or who said it, no matter if I have said it, unless it agrees with your own reason and your common sense."
- Buddha
|
|
IP Logged |
[ wu ] : http://wuriddles.com / http://forums.wuriddles.com
|
|
|
Brian Lee
Guest
|
|
Re: Triangles, missing area
« Reply #9 on: Nov 7th, 2002, 2:53pm » |
Quote Modify
Remove
|
on Jul 29th, 2002, 7:50pm, william wu wrote:"Believe nothing, no matter where you read it, or who said it, no matter if I have said it, unless it agrees with your own reason and your common sense."
- Buddha
|
|
Heh, you love that quote dontcha Wu? Well, it's definitely a good one... Yea I've seen this deceitful picture before on another forum... I heard its from a subway billboard somewhere in deutsche-land or something...
|
|
IP Logged |
|
|
|
wowbagger
Uberpuzzler
 
Gender:
Posts: 727
|
|
Re: Triangles, missing area
« Reply #10 on: Nov 8th, 2002, 2:32am » |
Quote Modify
|
Really? I haven't seen that picture IRL here in Germany ("Deutschland") yet. And yes, the quote is one you should always be aware of.
on Jul 26th, 2002, 3:32pm, S Spigarelli wrote:| The riddle is a big lie. It confused me until I realized that it was a lie, not a really fair riddle. |
|
I wouldn't go that far. Of course you can argue it's a lie to state the problem using "triangle" instead of "figure" or some other term. But it wouldn't be as puzzling then, would it?
Anyway, this is really a great riddle. A friend of mine who is a teacher once posed it to his class using an overhead projector and pieces cut from a transparency. It was quite a success...
|
| « Last Edit: Nov 8th, 2002, 2:33am by wowbagger » |
IP Logged |
"You're a jerk, <your surname>!"
|
|
|
CrisisAverted
Guest
|
|
Re: Triangles, missing area
« Reply #11 on: Dec 5th, 2002, 8:56pm » |
Quote Modify
Remove
|
I don't feel like bothering pulling out a ruler or doing sines, cosines, and tangents, so I'll fall back on the whole is equal to the sum of its parts. The area of each colored piece is the same in each triangle. A two dimensional shape only has the area of its component pieces, any shape with these pieces would always have the same area, provided there was no overlap. Compare shape one with shape two piece by piece and you can conclude that whatever shape one is, its not the same as shape two.
|
|
IP Logged |
|
|
|
i_m_n_idiot
Newbie
Posts: 6
|
|
Re: Triangles, missing area
« Reply #12 on: Jan 4th, 2003, 10:13pm » |
Quote Modify
|
hey i saw this iin a train
ppl from my country call it mrt or mtr
|
|
IP Logged |
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
The dewdrop slides into the shining Sea
Gender:
Posts: 4489
|
|
Re: Triangles, missing area
« Reply #13 on: May 3rd, 2003, 7:06pm » |
Quote Modify
|
There is a more general explanation of this apparent paradox in terms of Fibonacci numbers,
which are generated by the following recursive equation:
F(n+2) = F(n+1) + F(n), F(1) = F(2) = 1
producing the series 1,1,2,3,5,8,13,21,34,55,89............
Let the red triangle have horizontal and vertical sides of length F(n+1) and F(n-1), respectively.
Let the blue triangle have horizontal and vertical sides of length F(n+2) and F(n), respectively.
So that
in the upper figure the two triangles create a rectangle with an area of F(n)F(n+1)
and
in the lower figure the two triangles create a rectangle with an area of F(n-1)F(n+2)
Now consider the following Fibonacci identity:
F(n)F(n+1) - F(n-1)F(n+2) = +/- 1
Thus, the two rectangles are bound to differ in area by exactly one unit.
As n increases, the slopes of the hypotenuses of both triangles tend to the square of the Golden Ratio.
(phi2 = 0.3819660112...)
2/5 = 0.4 --> phi2 from above.
3/8 = 0.375 --> phi2 from below.
|
| « Last Edit: May 5th, 2011, 7:09am by ThudnBlunder » |
IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
SodiumPenathol
Newbie
Posts: 1
|
|
Re: Triangles, missing area
« Reply #14 on: Jan 18th, 2005, 12:20pm » |
Quote Modify
|
If you realize that the grid isn't made up of perfect squares it seems instantly obvious that it's an optical illusion. Just print the picture and try to fold it so that the opposite corners of the grid overlap each other perfectly. Then try to crease the paper smoothly along the fold. It can't be done without ripping the paper. Actually, doing this reveals the true ratio of the sides of the 'squares' as 13:14 or 14:15 (forgot). That's why the quote was inserted at the end.
|
|
IP Logged |
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
The dewdrop slides into the shining Sea
Gender:
Posts: 4489
|
|
Re: Triangles, missing area
« Reply #15 on: Jan 18th, 2005, 12:41pm » |
Quote Modify
|
Quote:| If you realize that the grid isn't made up of perfect squares |
|
Yes, it is.
At least, they are supposed to be perfect squares.
|
|
IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
|
Re: Triangles, missing area
« Reply #16 on: Jan 18th, 2005, 3:16pm » |
Quote Modify
|
Any vertical vs horizontal distortion you see is a result of the medium, not intrinsic to the puzzle. The squares are only added as a visual reference to make it easier to compare the two figures. You can reconstruct the puzzle on a grid you know to be square, and you will see that the puzzle still remains. The missing region is still there.
|
|
IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 7526
|
|
|
IP Logged |
|
|
|
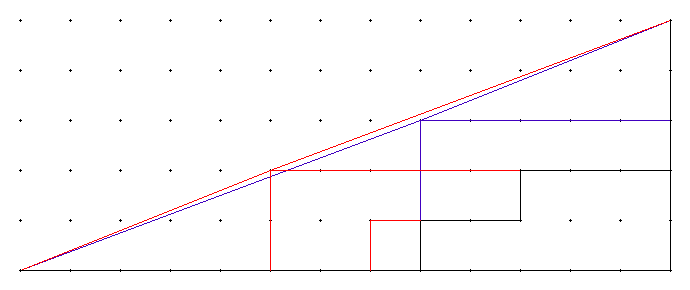
rmsgrey
Uberpuzzler
   
Gender:
Posts: 2872
|
|
Re: Triangles, missing area
« Reply #18 on: Jan 19th, 2005, 8:28am » |
Quote Modify
|
on Jan 18th, 2005, 12:20pm, SodiumPenathol wrote:| If you realize that the grid isn't made up of perfect squares it seems instantly obvious that it's an optical illusion. |
|
As long as both grids are the same shape, it doesn't matter what that precise shape is - though the picture is easier to follow if the lines are still straight.
Since there's no rotation of the component pieces, they're clearly the same shapes as long as all the individual cells are equivalent.
As Grimbal's post shows, superposing the two situations makes it clear both that the two grids are identical, and where the difference between the two shapes arises.
|
|
IP Logged |
|
|
|
OnlyAnEgg
Newbie
Gender:
Posts: 7
|
|
Re: Triangles, missing area
« Reply #19 on: Mar 8th, 2005, 9:41am » |
Quote Modify
|
Couldn't read Grimbal's post, but my approach was more like Magneeto's: when I added the component parts of "Triangle"1, they are A=(3x5) + (8x3)/2 + (5x2)/2 = 32.0 squares. But the entire figure gets A= (5 x 13)/2 = 32.5 squares. Chalk up the discrepancy to inaccurate figures, or optical illusions, I don't think it matters. My high school geometry teacher (Ed Cavey, SJ) always insisted that the proof cannot depend on the drawing, only the logic. So the areas of the two figures agree, and there is one square difference between them. 32+1=33<>32.5
|
|
IP Logged |
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
The dewdrop slides into the shining Sea
Gender:
Posts: 4489
|
|
Re: Triangles, missing area
« Reply #20 on: Mar 8th, 2005, 10:09am » |
Quote Modify
|
Quote:| Chalk up the discrepancy to inaccurate figures, or optical illusions |
|
No, chalk it up to assuming that the 'entire figure' is a triangle, rather than a quadrilateral.
|
| « Last Edit: Mar 8th, 2005, 11:18am by ThudnBlunder » |
IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print