Author |
Topic: Coloring the edges of an icosahedron (Read 17006 times) |
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender: 
Posts: 13730
|
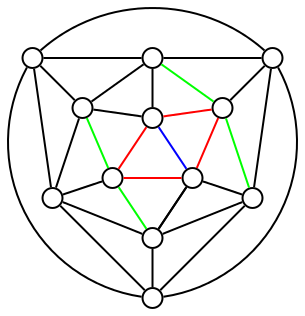
Is it possible, using (at most) four colors, to color the edges of an icosahedron in such a way that each edge's colors are different from those of its adjacent and opposite edges?
In the attached images, red edges are adjacent to the blue one (i.e. edges on the same triangle), and green ones are opposite the blue one (i.e. opposite on a quadrilateral made of two adjacent triangles).
|
| « Last Edit: Mar 24th, 2017, 1:25am by towr » |
 IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
rloginunix
Uberpuzzler
Posts: 1029
|
 |
Re: Coloring the edges of an icosahedron
« Reply #1 on: Mar 27th, 2017, 8:11am » |
 Quote  Modify
|
After an unsuccessful first attempt, I've constructed an isomorphic graph on straight edges only, to make the constraints compilation easier. Much size-reduced, not for detailed study but just to get an idea (image shows work in progress):
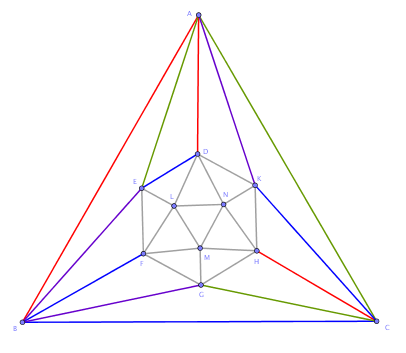
I'm taking that the solid is regular convex. Hence, each edge belongs to two (equilateral) triangles. Each triangle has two adjacent ones that carry one meaningful opposite edge each, for a total of 4 opposite edge constraints plus two sides of the same triangle constraints per triangle - another 4 constraints. For example, the edge on LN belongs to  LND, with opposite edges on DE and on DK, and to LNM, with opposite edges on MF and on MH: LN - {DE, DK, MF, MH}. The meaning of each item in the set - LN can *not* be assigned any of the colors currently set for DE, DK, MF, MH. Plus the edge on LN can not have the same color with the edges on LD, ND, LM, NM.
We pick 3 arbitrary (distinct) colors for any (initial) triangle and for the remaining edges we eliminate the impossible choices: if multiple colors for an edge are possible - we iterate (fork), if a possible color is unique then we set it and move on to the next edge, if no colors are possible then it's a dead end - we walk back up to the nearest fork, unsetting the colors along the way, and then repeat. That way, if we manage to assign a (legal) color to the 30-th edge then we are guaranteed a solution.
In my first attempt I have started with the innermost triangle and worked outward while in the second attempt I have started with 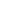ABC and worked inward, clockwise. For example, for my initial choice of color assignments the edge on AK (my starting edge) can be of only two colors: Red or Violet. However, I never managed to reach the 30-th edge: my best was something like 26/27 edges.
Neat idea. If it doesn't work out may be it's worth varying the solid or the constraints.
|
|
IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: Coloring the edges of an icosahedron
« Reply #2 on: Mar 27th, 2017, 10:54pm » |
Quote Modify
|
What I'd really hoped for, was that I could build an object like
without any of the elements its build from touching each other if they have the same color.
A single element looks like
And they assemble like
The actual constraint is a bit more relaxed than I posed here. You only need to exclude two of the "opposite" edges (either lefts, or rights, depending how you look at it)
Unfortunately, that doesn't seem to make it solvable either.
Unless, of course, I've translated the problem incorrectly.
|
| « Last Edit: Mar 28th, 2017, 8:55am by towr » |
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
dudiobugtron
Uberpuzzler
Posts: 735
|
|
Re: Coloring the edges of an icosahedron
« Reply #3 on: Mar 28th, 2017, 12:37am » |
Quote Modify
|
Just some initial musings:
Any suitable 4-colouring will need to have one colour on at least 8 edges, since there are 30 edges. (30/4 = 7.5) So I think a good approach to start with is to try to find 8 edges that aren't adjacent or opposite to each other; or to prove that it's impossible.
I see rloginunix has a cool S-shape strategy to get 7 edges, so it's getting pretty close!
|
| « Last Edit: Mar 28th, 2017, 1:24am by dudiobugtron » |
IP Logged |
|
|
|
rloginunix
Uberpuzzler
Posts: 1029
|
|
Re: Coloring the edges of an icosahedron
« Reply #4 on: Mar 28th, 2017, 8:22am » |
Quote Modify
|
I think that towr's translation is perfectly fine - most likely the origami folks are being loose with the instructions language which may be fine in an everyday sense but is not tight enough mathematically (even in some hard science textbooks we occasionally find the "this page intentionally left blank" pearls).
In any case, I am afraid that I am the bearer of bad news: finished the brute force enumeration - no cigar with the original 4+4 constraints requirement (unless I made some silly mistake).
|
|
IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: Coloring the edges of an icosahedron
« Reply #5 on: Mar 28th, 2017, 8:55am » |
Quote Modify
|
It's a shame I don't have a fifth color. Then it would be easy, and I could have equal numbers of each color.
|
|
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
rloginunix
Uberpuzzler
Posts: 1029
|
|
Re: Coloring the edges of an icosahedron
« Reply #6 on: Mar 28th, 2017, 11:35am » |
Quote Modify
|
What prevents you from introducing the fifth color?
|
|
IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: Coloring the edges of an icosahedron
« Reply #7 on: Mar 28th, 2017, 12:34pm » |
Quote Modify
|
Literally, physically not having it.
I only have 4 colors of quality paper that go well together. And I haven't even been able to find more of those recently, let alone other colors.
I like using constructions like this as gift-wrapping, so not just any colored paper will do.
(On the other hand, I've never had any complaints about elements of the same color touching, so that's really just for my own peace of mind.)
|
| « Last Edit: Mar 28th, 2017, 1:13pm by towr » |
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 7526
|
|
Re: Coloring the edges of an icosahedron
« Reply #9 on: May 7th, 2017, 6:53am » |
Quote Modify
|
Anyway, I wrote a program to search a solution with the relaxed rule (colors are excluded within any "Z" pattern).
What came out is that you need to allow 2 exceptions to the rule to complete the star.
Actually, if you look at a single color, you can color at most 7 edges without creating a conflict. So with 4 colors you can color up to 28 edges without a conflict. But you have 30 edges.
It is a pitty you don't have 5 colors, you could do a perfectly symmetrical configuration. But you probably know that.
|
| « Last Edit: May 7th, 2017, 1:39pm by Grimbal » |
IP Logged |
|
|
|
Arne
Newbie
Welcome
Gender:
Posts: 6
|
|
Re: Coloring the edges of an icosahedron
« Reply #10 on: Jun 13th, 2017, 10:54am » |
Quote Modify
|
I might be missing something completely obvious but here has to be a way to color it right? If you would convert the edges to nodes & notes to edges this would be covered by the four color theorem https://en.wikipedia.org/wiki/Four_color_theorem. And my gut feeling is that the conversion of nodes to edges and back again after coloring it would be "legal" creating valid graphs.
|
|
IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: Coloring the edges of an icosahedron
« Reply #11 on: Jun 13th, 2017, 12:51pm » |
Quote Modify
|
The four color theorem doesn't apply. The problem is that this isn't like a simple map of contiguous regions/countries. But each country has enclaves that need to have the same color as the parent country. That additional constraint makes it that the four color theorem doesn't work.
|
|
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print