 Author
Author |
Topic: n prisoners and a k-state switch (Read 7032 times) |
|
Hippo
Uberpuzzler
    

Gender: 
Posts: 919
|
 |
n prisoners and a k-state switch
« on: Apr 26th, 2007, 3:40am » |
 Quote Quote  Modify Modify
|
This is generalisation of 5 prisoners and a light bulb and 100 prisoners and two bulb riddle:
There are n prisoners in the prison, once warden defines rules, the prisoners can discuss their strategy and when done, they are sent to their solitary cells. They cannot receive any information when they are on their cells.
The warden takes a prisoner with probability 1/n into its office. The prisoner can see the state of the communication switch and left the switch in an arbitrary state, than the prisoner is put back into his cell. Warden cleans the office so no more info can be left in the office. At some time, a prisoner can declare he has a proof all of them were in the cell.
He describes the communication strategy and that his observations can be fulfilled only if all prisoners were there, providing they followed the strategy.
Warden compares the order of choosing prisoners and their behaviour and if it corresponds to the strategy, all prisoners are made free.
There are 3 variants of the problem:
A) The prisoners are provided with visit count (one per day visit).
B) No visit count but initial state of the switch is known.
C) No visit count, initial state of the switch is unknown.
Of course k>1.
The strategy is measured by average number of visits required to declare proof.
The goal is to find the strategy with the average as small as possible.
100A2 is the 100 prisoners and a light bulb problem.
5A2 is the 5 prisoners and a light bulb problem.
100C4 is the 100 prisoners and two light bulb problem.
What I am interested in are questions like
for which n the optimal algorithm for nA2 problem is the one counter method with 2-3day hooked snowball prephase? Or better which of known algorithms for 100A2 problems are best for other n in nA2 algorithm.
There is a lot of other interesting questions here.
|
| « Last Edit: Feb 20th, 2009, 5:50am by Hippo » |
 IP Logged IP Logged |
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 7527
|
 |
Re: n prisoners and a k-state switch
« Reply #1 on: Apr 26th, 2007, 7:21am » |
 Quote Quote  Modify Modify
|
For a starter, k>=n is not very hard. Even if the initial state is unknown.
|
|
 IP Logged IP Logged |
|
|
|
Hippo
Uberpuzzler
    

Gender: 
Posts: 919
|
 |
Re: n prisoners and a k-state switch
« Reply #2 on: Apr 27th, 2007, 1:18am » |
 Quote Quote  Modify Modify
|
Grimbal: You are right  , but please follow these conventions: , but please follow these conventions:
nAk: for k>=n is easy ...
nBk: for k>=n is easy ...
nCk: for k>=n is easy ...
Please give details for nCk case ... it does not seem to be so trivial to me (to use optimal algorithm).
|
| « Last Edit: Apr 27th, 2007, 1:22am by Hippo » |
 IP Logged IP Logged |
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 7527
|
 |
Re: n prisoners and a k-state switch
« Reply #3 on: Apr 27th, 2007, 1:45am » |
 Quote Quote  Modify Modify
|
OK, the trick for nCk, k>=n (which covers A and B) is as follows:
Number the switch states from 0 to k-1.
On the first visit, a prisoner remembers the switch state as s0 and moves the switch to state s0+1 (mod k).
After that, as soon as he sees the switch in state s0+n (mod k), he knows everybody was there.
|
|
 IP Logged IP Logged |
|
|
|
Hippo
Uberpuzzler
    

Gender: 
Posts: 919
|
 |
Re: n prisoners and a k-state switch
« Reply #4 on: Apr 27th, 2007, 3:31am » |
 Quote Quote  Modify Modify
|
OK for nAk,nBk where it is trivial, for the nCk case:
Well done for k=n or slightly greater. But neednot be optimal for k>>n.
If the first prisoner returns to office before all other, it may be valuable to left the message here so the win condition can be declared by the second prisoner ...
Win condition can be declared by someone who entered office before and all other prisoners were there after that visit. For huge k, this can be detected on the first such occassion. How huge the k should be? What is minimal such k?
|
| « Last Edit: Apr 27th, 2007, 4:33am by Hippo » |
 IP Logged IP Logged |
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 7527
|
 |
Re: n prisoners and a k-state switch
« Reply #5 on: Apr 27th, 2007, 6:00am » |
 Quote Quote  Modify Modify
|
If there is no visit count and the initial state isn't known, there is no way for a prisoner who enters for the first time to know if anybody has been here before. A win can only be detected by someone who enters for the second time, and based on the difference between how he left the switch and how he finds it.
If k = an, they can express k in base a to get n digits. Each prisoner can change his own digit every time he visits the room, and remember which other digits changed. When someone has seen all digits change, he knows everyone was in.
|
|
 IP Logged IP Logged |
|
|
|
Hippo
Uberpuzzler
    

Gender: 
Posts: 919
|
 |
Re: n prisoners and a k-state switch
« Reply #6 on: Apr 27th, 2007, 6:33am » |
 Quote Quote  Modify Modify
|
Well done, it seemed to be optimal solution and it also shows no such huge k exists to be able to guarantee the optimal time.
The difference of its average time and average optimal time will be very very small.
So we can concentrate to cases with k<n 
OK I should correct it a bit ... I am not sure ... for what a and n this algorithm is faster in average than original one?
So ... let us continue with nCk case when k>=n2n. Take maximum a such that k>=nan. And work with the vector n x a x a x a x ... x a.
When prisoner enters first time, he increments first coordinate (mod n) and allocates corresponding coordinate (say p) for himself and sets his knowledge to k=p. He may also increment p-th coordinate (mod a). Following visits he only increments p-th coordinate (mod a). Except playing with switch a prisoner p improves his knowledge k ... he remembers switch state from the first visit. Surely there vere prisoners from k to current first coordinate. But if another coordinate outside this range was changed, he knows corresponding prisoner p' was near the swith before him and decreases k=p' (mod n). If k equals first switch coordinate, we are done.
Of course switch state outside of communication range, means this is the first visit so the prisoner can turn the switch into arbitrary position in comunication range and start pretending he enters with the switch in this position.
|
| « Last Edit: May 7th, 2007, 1:08am by Hippo » |
 IP Logged IP Logged |
|
|
|
Hippo
Uberpuzzler
    

Gender: 
Posts: 919
|
 |
Re: n prisoners and a k-state switch
« Reply #7 on: May 7th, 2007, 1:59am » |
 Quote Quote  Modify Modify
|
So for the start with small k: (all nAk,nBk,nCk cases).
Start with nBk case:
Even if we don't use phases (the difference between nAk and nBk) the tokens/badges signalling can be used if we use k-1 kinds of signals. Prisorer each time chooses which kind of token to pass or not to pass any of them.
I guess passing allways the token of minimal value is the best choice.
This leads to k-1 level hierarchy choosing r=(k-1) th root of n as a base. Tokens represent 1,r,r2,r3,...
Of course there are rounding errors so one should adopt this scheme a little bit. (I prefere rounding to have bigger goals when the number of counters is bigger.) ... to be thought about
If we want to use binary signalling for top levels and n>2k-1, we should decrease number of signals for level signalling therefore increase r. I am not sure how valuable it will be.
Let us consider case nBk for n<2k-1 in other posts.
There are problems with snowball prephases as each day the signal meaning differ, so snawballs are probably not usable in the nBk, nCk cases (for small k). On the contrary for the nAk case the snowballs are very useful. We can increase number of possible signals as we know the visit count in the A case. The most clear method is to use "phases" in the nAk case. Than the problems with propper timing for phase switching arises....
For the nCk case the nBk method can be adopted with the following hook: Whenever we create one token in the nBk case, we create two tokens now.
Total goal on each level should be twice the original goal. This mades the one possible additional starting token of any level not to be suitable to cause premature end.
|
| « Last Edit: May 9th, 2007, 2:42pm by Hippo » |
 IP Logged IP Logged |
|
|
|
Hippo
Uberpuzzler
    

Gender: 
Posts: 919
|
 |
Re: n prisoners and a k-state switch
« Reply #8 on: May 9th, 2007, 2:20pm » |
 Quote Quote  Modify Modify
|
snowball signalling:
nBk for 1+log2n<=k case, leads to binary signalling. There are k-(1+log2n) unused switch positions. They can be used for "snowball" signalling.
It seems to me, that good set of signals is passing 1,2,3,4,...,2b-1,2b,2b+1,...2c-1 tokens where c is minimal such 2c>n.
(There are distributed 2c tokens at the beginning).
If the number of tokens you have mod 2b is nonzero, send this modulo. Otherwise use "minimal possible signalling".
for nCk case snowball signalling seems to be impossible at all (but for k>n resp. k>nan we have seen simillar method).
For nAk case the snowball signalling can be modified by k-switch, too. Switch position can denote the number of missed tokens ...
|
| « Last Edit: May 9th, 2007, 2:24pm by Hippo » |
 IP Logged IP Logged |
|
|
|
Hippo
Uberpuzzler
    

Gender: 
Posts: 919
|
 |
Re: n prisoners and a k-state switch
« Reply #9 on: May 9th, 2007, 2:35pm » |
 Quote Quote  Modify Modify
|
What remain to discuss?
It seems to me that mainly nAk cases and phase switching problems.
After initial snowball phases ... for how big n for given k using phase switching improves the average time ...
BTW: Observers method usefull for nA2 case is probably unusable for nAk case for k>2 (at least when we are sending the smallest possible binary signal).
|
| « Last Edit: May 9th, 2007, 2:41pm by Hippo » |
 IP Logged IP Logged |
|
|
|
Hippo
Uberpuzzler
    

Gender: 
Posts: 919
|
 |
Re: n prisoners and a k-state switch
« Reply #10 on: Nov 13th, 2008, 1:59pm » |
 Quote Quote  Modify Modify
|
Currently I am working on nA2 case for small n.
It seemed two level counting (one counter level and one binary level with "binary observers") gets almost the same average for n around 19 or 20. For smaller n one counter with snowroll is faster, for higher n two level counting is better.
[edit]
Even for 18A2 case 2 counters with binary observers are faster than single counter.
(5:0:10,4:1:8|201,214||126| gets around 293 days compared to 299.46 got by 8:0:18| ) )
Even for 17A2 case 2 counters with binary observers are faster than single counter.
(5:0:9,3:1:8|182,173||96| gets around 256 days compared to one counter with snowroll and 2/3 day hook 267.26 got by 8:0:17| ) . Current generation average is 258.89 and whole simulation average 262.23. ) . Current generation average is 258.89 and whole simulation average 262.23.
[/edit]
|
| « Last Edit: Nov 20th, 2008, 2:52am by Hippo » |
 IP Logged IP Logged |
|
|
|
Hippo
Uberpuzzler
    

Gender: 
Posts: 919
|
 |
Re: n prisoners and a k-state switch
« Reply #11 on: Jan 12th, 2009, 1:22am » |
 Quote Quote  Modify Modify
|
Current state of the simulations for n2A case:
Days for so far best algorithms:
1A2:1 
2A2:3 (=binary/ignore first)
3A2:5.5 (=binary, ignore first)
4A2:12.3 (=ternary, ignore first)
Following results are rounded (what covers I hope unary observers improvements ... actually not calculated)
5A2: 23.26 (3:0:5|* single counter with 3 nights snowball and first possible fail hook)
6A2: 33.76 (4:0:6|*)
7A2: 45.90 (4:0:7|*)
8A2: 60.01 (5:0:8|*)
9A2: 75.72 (5:0:9|*)
10A2: 93.39 (5:0:10|*)
11A2: 112.76 (6:0:11|*)
12A2: 133.97 (6:0:12|*)
13A2: 157.05 (7:0:13|*)
14A2: 181.82 (7:0:14|*)
15A2: 208.52 (7:0:15|*)
Following results are experimental so only aproximate values (I hope it's upper bound) and even the parameters neednot be the best ones:
16A2: 233 (6:0:9,3:1:7|166,193||82| two counters with binary "observers" (and first fail hook and careful snowball restarting) ... actually observres does not improve 2 counters case and one counter algorithm (8:0:16|*) gets 236.99.)
17A2: 257.6 (5:0:9,3:1:8|182,173||96|)
18A2: 292.7 (5:0:10,4:1:8|201,214||126|)
19A2: 307.9 (5:0:10,5:1:9|229,196||100|)
20A2: 341.7 (5:0:10,4:1:10|251,242||125|)
21A2: ?
22A2: ?
23A2: 425.34 (7:0:12,5:1:11|307,255||119|)
(Two counters beats 4 counters by around 13 days.)
24A2: 455.81 (5:0:7,4:0:6,4:1:6,2:1:5|299,243|136|134|114 four counters with binary /\// observers (and first fail hook and careful snowball restarting) beats two counters by around 8 days)
I didn't experiment with 3 counters and ternary top phase, or with two counting layers.
|
| « Last Edit: Jan 12th, 2009, 1:26am by Hippo » |
 IP Logged IP Logged |
|
|
|
Hippo
Uberpuzzler
    

Gender: 
Posts: 919
|
 |
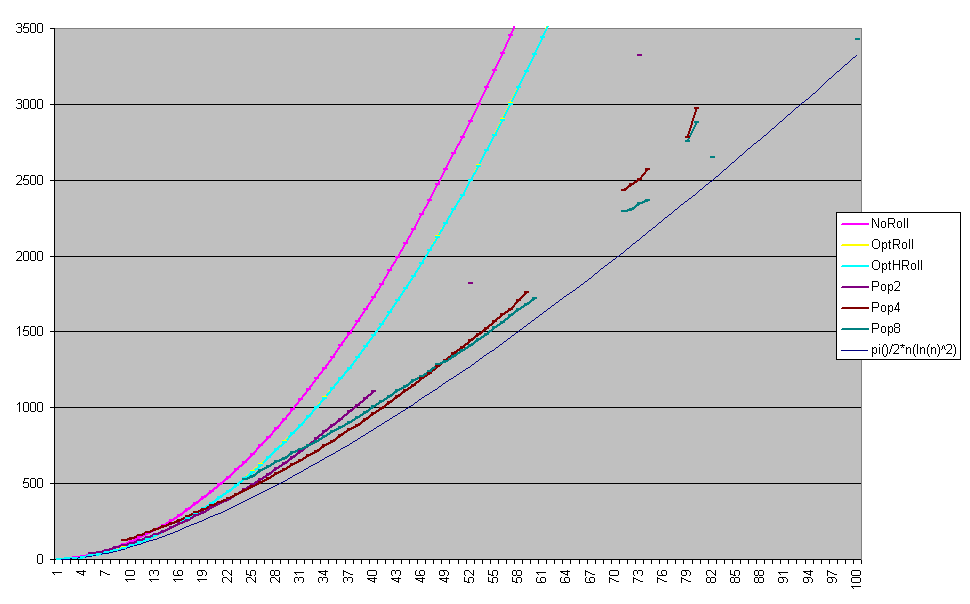
Re: n prisoners and a k-state switch  nA2.PNG nA2.PNG
« Reply #12 on: Jan 27th, 2009, 10:35am » |
 Quote Quote  Modify Modify
|
I have improved the initialisation (scaling so far best results from problems with different n)
and changed mutation algorithm to "sexy" genetic one and run few generations for several cases.
Here is the graph of averages of all runs (of all gen's) of the algorithms.
To be updated later according to simulation progress.
(At least two level counting scheme with different number of counters should be tested for n above 20, three counters with ternary counting for small n should be tested as well).
|
| « Last Edit: Jan 27th, 2009, 10:44am by Hippo » |
 IP Logged IP Logged |
|
|
|
Hippo
Uberpuzzler
    

Gender: 
Posts: 919
|
 |
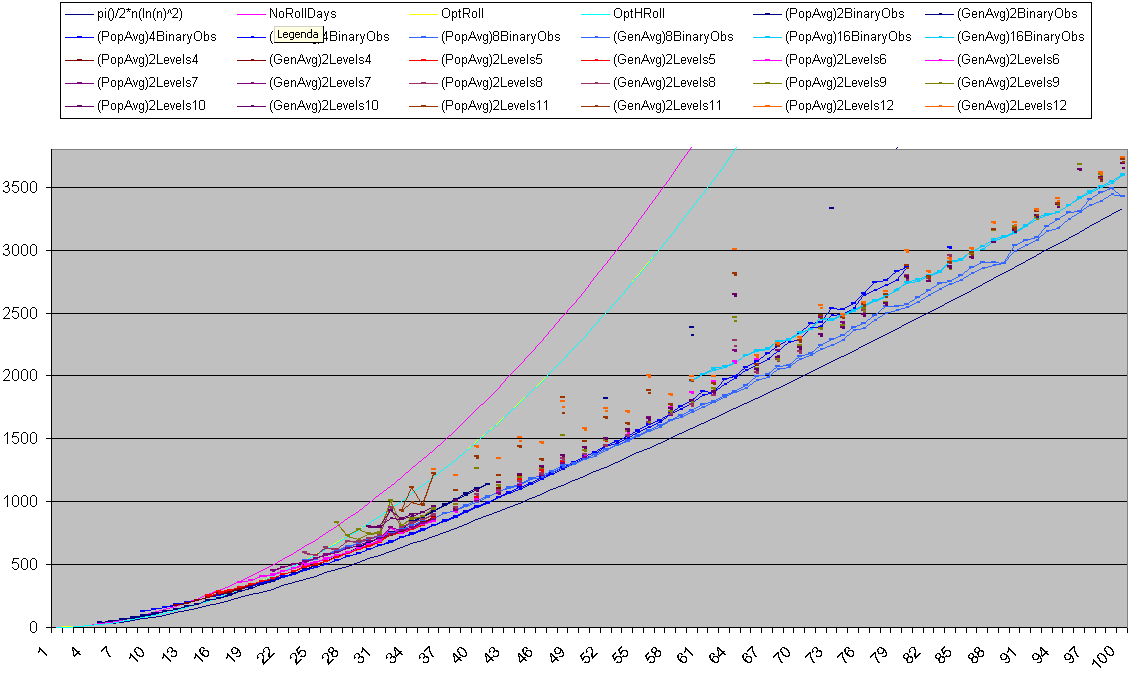
Re: n prisoners and a k-state switch  nA2c.png nA2c.png
« Reply #13 on: Feb 5th, 2009, 12:58am » |
 Quote Quote  Modify Modify
|
I have an actualisation of simulation results. Ternary counting not implemented yet. The binary observers seems to beat two level counting.
|
|
 IP Logged IP Logged |
|
|
|
Hippo
Uberpuzzler
    

Gender: 
Posts: 919
|
 |
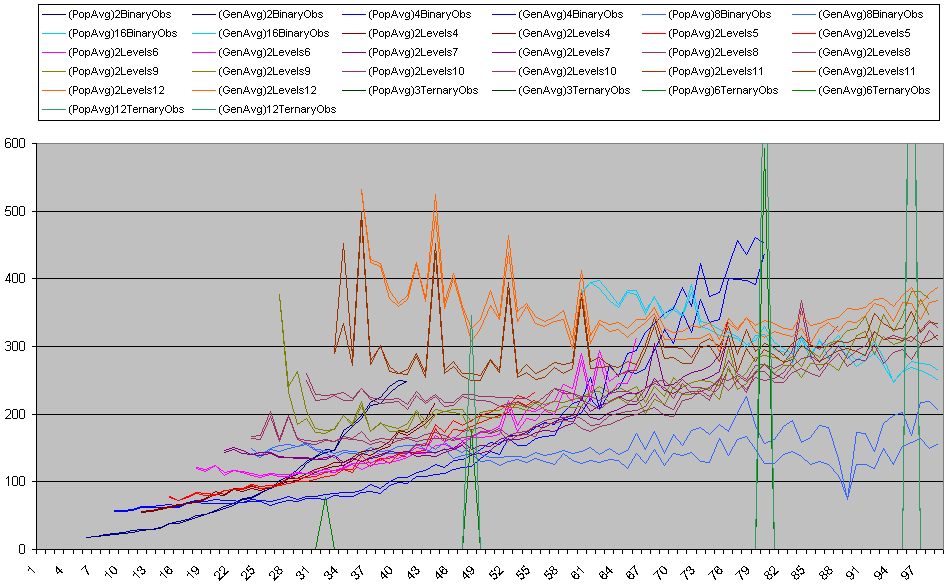
Re: n prisoners and a k-state switch  NA2d.PNG NA2d.PNG
« Reply #14 on: Feb 10th, 2009, 1:55am » |
 Quote Quote  Modify Modify
|
New results in different view: function ( /2)n ln2 n subtracted. /2)n ln2 n subtracted.
I have started simulation for binary observers with ternary top phase.
Wow, after removing bugs from ternary top simulation, it seems ternary top with observers is even better than binary!
I didn't expected so as the information is not spread as well in the ternary top case, but saving one phase is important.
It behaves well even for 12 counters!
Experiments in progress.
There is one thing surprising about the snowball prephases (in ternary cases).
Best gens have either format 5:0:10,5:0:9,5:0:8,5:0:8,5:0:8,5:0:8,5:0:7,5:0:7,5:0:7,5:0:7,5:0:7,5:0:7 with "long snowballs" and no double badge prevention at all
or format 3:0:8,3:1:8,3:1:8,3:1:8,3:1:8,3:1:8,3:1:8,3:1:8,3:1:8,3:1:8,3:1:7,3:1:7 with short snawballs and maximal double badge prevention.
May be its due to short genetic process, but there were gen's with mixed prephases and all of them were beaten.
|
| « Last Edit: Feb 20th, 2009, 5:00am by Hippo » |
 IP Logged IP Logged |
|
|
|
Hippo
Uberpuzzler
    

Gender: 
Posts: 919
|
 |
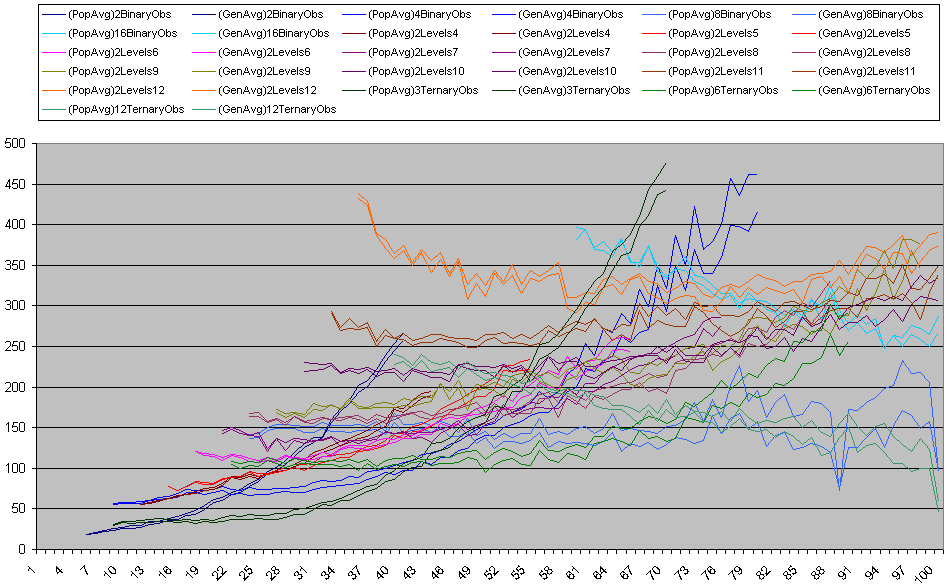
Re: n prisoners and a k-state switch  na2d2.PNG na2d2.PNG
« Reply #15 on: Feb 20th, 2009, 5:13am » |
 Quote Quote  Modify Modify
|
P.S.: You can see exceptional behaviour for 8binary and n=89, 8binary and 12ternary and n=100 (actually not on the previous graph) and 16binary and n=94. Its due to simulation of these for longer time than the others.
You can see what the longer simulation does ... the last generation average becomes almost equal to all population average and it is less than for short simulation (roughly the difference between population average and last generation average should be subtracted). This is actually above the best gen averages, but they are affected by small number of simulations as well.
|
| « Last Edit: Feb 20th, 2009, 5:17am by Hippo » |
 IP Logged IP Logged |
|
|
|
Hippo
Uberpuzzler
    

Gender: 
Posts: 919
|
 |
Re: n prisoners and a k-state switch
« Reply #16 on: Aug 3rd, 2010, 11:45pm » |
 Quote Quote  Modify Modify
|
For the nC2 case I continue with the ideas from http://www.ocf.berkeley.edu/~wwu/cgi-bin/yabb/YaBB.cgi?board=riddles_har d;action=display;num=1203963868 thread:
Only counter can declare end so he can calculate probabilities of information spread among other prisoners:
Let n.. be number of drones never being in the cell, n+. number of drones being in cell only with switch on, n.- number of drones being in cell only with switch off, n+- active prisoners wiling to turn on and nd number of drones whose job is already done.
As n..+n+.+n.-+n+-+nd+1=n, nd could be deduced from others.
When counter is in the room, unknown state of the system can be described by vector (n..,n+.,n.-,n+-).
Counter knows his visit history switch states on entrance and switch states when he leaves.
So counter can for each history calculate probabilities of possible unknown states.
For optimising counter strategy we are not concerned on the number of drones visits, but only on number of counter visits. So our task is to go from either (1/n)(n-k-1,k,0,0) + or (1/n)(n-k-1,0,k,0) - to (0,0,0,0) h with as short history h as possible (on average).
With switch on it goes from (n..,n+.,n.-,n+-) to
(n..-k.,n+.+k.,n.--k-,n+-+k[sub ]-[/sub]) (and switch on) with probability 1/(1+n..+n.-)*Choose (n.. over k.)*Choose (n.- over k-)/Choose (n..+n.- over k.+k-).
With switch off the situation is a bit more complicated.
Seems I must change notation to x for n.., m for n.-, p for n+. and b for n+-.
With switch on it goes from (x,p,m,b) to
(x-k,p+k,m-l,b+l) (and switch on) with probability 1/(1+x+m)*Cxk*Cml/Cx+mk+l.
Similarly with switch off knowing nobody switched on:
It goes from (x,p,m,b) to
(x-k,p-l,m+k,b+l) with probability 1/(1+x+p)*Cxk*Cpl/Cx+pk+l.
So the most complicated case when some drone switch on remains ...
Oops p and b acts equally when switch is off. It would be easier, the last formula has no sense for l>0.
|
| « Last Edit: Aug 8th, 2010, 12:55am by Hippo » |
 IP Logged IP Logged |
|
|
|
Hippo
Uberpuzzler
    

Gender: 
Posts: 919
|
 |
Re: n prisoners and a k-state switch
« Reply #17 on: Aug 4th, 2010, 4:58am » |
 Quote Quote  Modify Modify
|
So once again nC2 formalism:
Unknown state for the counter is (i,a,d) where i+a+d+1=n; i is number of drones never seeing switch on, a is number of drones whose have seen switch on, but which didn't switch it and d are drones which already manipulated the switch.
With switch on (i,a) wents to (i-k,a+k) with probability 1/(i+1), and with switch off it goes with proability 1/(a+1) to switch off and conditional transition probablity of (i,a) is 1, and with probability a/(a+1) switch changes to on and in that case conditional transition probabilities to (i-k,a+k-1) become 1/(i+1).
So with this base we can study the shortest counter history in avereage problem...
((Starting either in (n-1,0) off state or in (n-1-k,k) on state with probability 1/n) and going to (0,0)).
OOOOPS, the shortest counter history average is interesting on its own, but as the probabilities are not independent to lengths among counter visits it would not guarantee optimal strategy for n2C problem 
Never mind ... let us continue ...
with d known to counter i=n-1-d-a so just (a) suffices to describe the unknown state.
Let pa be probability the unknown state is (n-1-d-a,a) or shortly (a). \suma pa=1.
If the counter left room with switch off the total probability switch remain off is \suma pa/(a+1) so knowing switch remain off rebalances our probabilities to p'a=(pa/(a+1))/\sumb(pb/(b+1)).
Similarly for switch changed to on rebalances original probabilities to p'a=apa/(a+1)/sumb(bpb/(b+1)).
So the resulting probabilities of (n-1-(d+1)-a,a) are p''a=\sumb\le a+1p'b/(n-d-b)=\sumb\le a+1bpb/((b+1)(n-d-b)\sumccpc/(c+1)).
Leaving counter in on state results in counter in on state next visit, but probabilities p'a are changed to \sumb\le apb/(n-d-b).
|
| « Last Edit: Aug 8th, 2010, 12:56am by Hippo » |
 IP Logged IP Logged |
|
|
|
Hippo
Uberpuzzler
    

Gender: 
Posts: 919
|
 |
Re: n prisoners and a k-state switch
« Reply #18 on: Aug 8th, 2010, 12:54am » |
 Quote Quote  Modify Modify
|
So for nC2 case (n>2 as 2C2 was already solved by Grimbal) I am not sure the following algorithm is optimal, but it's my favorite:
Select one counter everyone else is drone.
Dron does nothing until he has seen switch-on what activates him. Active drone waits until he enters with switch-off. In that case he switches to on and enters "done" state. In done state drone ignores the switch at all.
Counter algorithm is much more sophisticated. He estimates the probability there are a drones active by the formulas mentioned on previous post.
Counter remembers switch state he left in the room and counts changes on return so he has perfect information about drones in "done" state. Until half drones are in "done" state, he lefts switch off whenever probability some drone switches it on is at least 1/2. After half drones are in "done" state, he lefts the switch off when probability no drone is active is less than 1/2.
Suppose counter does not use exact arithmetics, there is problem with rounding errors. If the tiny probability no drone is active is rounded to 0, the algorithm would never terminate. So one must take care to prevent this rounding.
|
| « Last Edit: Nov 30th, 2010, 5:53am by Hippo » |
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register