Author |
Topic: (71-1)(71+1) = 71 (Read 13229 times) |
|
Grimbal
wu::riddles Moderator
Uberpuzzler
Gender: 
Posts: 7526
|
Here is an equation: (71-1)(71+1) = 71
The astute reader will notice it is not true.
How can you make it a valid identity by adding
(a) a single dot
or (b) two dots
or (c) a single straight line.
Notes
1. For this problem, the 1 is a straight line, the 7 are 2 straight lines.
2. I want an IDENTITY. Adding / on = is not an option.
[edit: change equation to identity]
|
| « Last Edit: Aug 1st, 2004, 7:32am by Grimbal » |
 IP Logged |
|
|
|
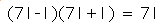
honkyboy
Junior Member
Gender:
Posts: 101
|
 |
Re: (71-1)(71+1) = 71
« Reply #1 on: Jul 31st, 2004, 4:06pm » |
 Quote  Modify
|
for a single dot (a)
(71-1)(71+1)=7!
A redundant dot could be added for two (not the intended answer I'm sure)
(71-1).(71+1)=7!
|
|
IP Logged |
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 7526
|
|
Re: (71-1)(71+1) = 71
« Reply #2 on: Jul 31st, 2004, 4:26pm » |
Quote Modify
|
So fast? Too bad.
Even though I asked only one option, and this was the intended slution, on another forum we foud a solution for all 3 cases.
So keep searching.
|
|
IP Logged |
|
|
|
Sir Col
Uberpuzzler
impudens simia et macrologus profundus fabulae
Gender:
Posts: 1825
|
|
Re: (71-1)(71+1) = 71
« Reply #3 on: Aug 1st, 2004, 3:55am » |
Quote Modify
|
If we don't have to state the base (4969), we could write (71-1)(71+1)[equiv]71? 
It may just be semantics, but 3+4=7 is an identity, not an equation. An identity is true for all values, whereas an equation must contain a variable and is true for some, or none, of the values. For example, x=3, is an equation, because x need not always be 3; 3x+4x=7x is an identity, because it is true for all values of x.
So how about the equation... (71-L)(71+1)=71?
|
|
IP Logged |
mathschallenge.net / projecteuler.net
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 7526
|
|
Re: (71-1)(71+1) = 71
« Reply #4 on: Aug 1st, 2004, 7:30am » |
Quote Modify
|
OK, ok,  I want an identity, then.
|
|
IP Logged |
|
|
|
Sir Col
Uberpuzzler
impudens simia et macrologus profundus fabulae
Gender:
Posts: 1825
|
|
Re: (71-1)(71+1) = 71
« Reply #5 on: Aug 1st, 2004, 8:00am » |
Quote Modify
|
Sorry, I wasn't criticising.
I realised my "answer" wasn't what you were after, but I've been working on the single line part and I am still having difficulties. I don't suppose you would accept an inequality either... (71-1)(71+1)[ge]71? 
|
|
IP Logged |
mathschallenge.net / projecteuler.net
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 7526
|
|
Re: (71-1)(71+1) = 71
« Reply #6 on: Aug 1st, 2004, 2:15pm » |
Quote Modify
|
EQUALITY! That is what I meant by equation.
So, no inequality either.
|
|
IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
|
Re: (71-1)(71+1) = 71
« Reply #7 on: Aug 3rd, 2004, 9:32pm » |
Quote Modify
|
on Aug 1st, 2004, 3:55am, Sir Col wrote:| 3+4=7 is an identity, not an equation ... an equation must contain a variable |
|
What? By the definitions I've always used, an equation is a statement of the form "A = B", where A and B are any valid expressions. 3+4=7 most certainly IS an equation, as is 3+4=89. The latter is false, but it is still an equation. There is no requirement that a variable be present. All that is required is that the statement equate two things.
|
|
IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: (71-1)(71+1) = 71
« Reply #8 on: Aug 4th, 2004, 12:21am » |
Quote Modify
|
Quote:
|
| « Last Edit: Aug 4th, 2004, 12:22am by towr » |
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Sir Col
Uberpuzzler
impudens simia et macrologus profundus fabulae
Gender:
Posts: 1825
|
|
Re: (71-1)(71+1) = 71
« Reply #9 on: Aug 4th, 2004, 3:25am » |
Quote Modify
|
I got all excited when I saw that someone had posted here, thinking they had found a solution to Grimbal's last question.
We've been down this road before, but... 
Quote: http://en.wikipedia.org/wiki/Equation
In mathematics, one often (not quite always) distinguishes between an identity, which is an assertion that two expressions are equal regardless of the values of any variables that occur within them, and an equation, which may be true for only some (or none) of the values of any such variables. In equations, the values of the variables for which the equation is true are called solutions. |
|
However, I checked in my (Collins) Mathematical Dictionary and it makes an interesting distinction...
Quote:| Equation, n a formula that asserts that two expressions have the same value; it is either an identical equation (usually called an IDENTITY), which is true for any values of the variables, or a conditional equation, which is only true for certain values of the variables (the ROOTS of the equation). For example, x2-1=(x+1)(x-1) is an identity, and x2-1=3 is a conditional equation, with roots [pm]2. |
|
In light of this, I concede that my original objection was a little pedantic. However, I've learned something new; and I don't mean that I am pedantic. (I already knew that!)
|
|
IP Logged |
mathschallenge.net / projecteuler.net
|
|
|
honkyboy
Junior Member
Gender:
Posts: 101
|
|
Re: (71-1)(71+1) = 71
« Reply #10 on: Aug 4th, 2004, 11:17am » |
Quote Modify
|
I am stumped on the single straight line. How about this solution for four dots:(71-1)::(71+1)=71
|
| « Last Edit: Aug 4th, 2004, 11:18am by honkyboy » |
IP Logged |
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 7526
|
|
Re: (71-1)(71+1) = 71
« Reply #11 on: Aug 4th, 2004, 12:24pm » |
Quote Modify
|
A hint:
->The 2-dot solution is most likely to be found by a physicist...
The straight-line one more by ... well ... a typographer.
<-
|
|
IP Logged |
|
|
|
Leo Broukhis
Senior Riddler
Gender:
Posts: 459
|
|
Re: (71-1)(71+1) = 71
« Reply #12 on: Aug 4th, 2004, 7:32pm » |
Quote Modify
|
on Aug 4th, 2004, 11:17am, honkyboy wrote:| I am stumped on the single straight line. How about this solution for four dots:(71-1)::(71+1)=71 |
|
I am not familiar with this notation. What do 4 dots mean? A missing element of a sequence?
|
|
IP Logged |
|
|
|
Leo Broukhis
Senior Riddler
Gender:
Posts: 459
|
|
Re: (71-1)(71+1) = 71
« Reply #13 on: Aug 4th, 2004, 7:33pm » |
Quote Modify
|
Grimbal, are you implying an overbar?
|
|
IP Logged |
|
|
|
honkyboy
Junior Member
Gender:
Posts: 101
|
|
Re: (71-1)(71+1) = 71
« Reply #14 on: Aug 4th, 2004, 7:37pm » |
Quote Modify
|
Four dot is for arithmetic mean.
4::6=5. the average of four and six is five.
|
|
IP Logged |
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 7526
|
|
Re: (71-1)(71+1) = 71
« Reply #15 on: Aug 14th, 2004, 4:41pm » |
Quote Modify
|
Ok, here are my answers.
(a) (71-1)(71+1) = 7!
(b) put a dot over the first 1 and over the second 71.
A dot is a derivation relative to time d/dt. For constants, it is zero.
(c) (71-1)(71+1) = 71
or (71-1)(71+1) = 71
|
| « Last Edit: Aug 14th, 2004, 4:43pm by Grimbal » |
IP Logged |
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print