Author |
Topic: Area Of a Circle (Read 8618 times) |
|
Obob
Senior Riddler
Gender: 
Posts: 489
|
 |
Re: Area Of a Circle
« Reply #25 on: Sep 11th, 2007, 3:25pm » |
 Quote  Modify
|
Well you can do differentiation of polynomials without knowing about limits. You can't prove your answer is correct (not that you even know what correct means, since you can't define derivative), but at least you can differentiate them.
Strangely enough, differentiation of polynomials is actually an important concept in algebraic geometry, which is a field of math where you can talk about curves and stuff over number systems other than the real or complex numbers, where there is no notion of limits. You simply define the derivative of the polynomial to be what you would expect it to be in the real or complex case.
|
|
 IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
|
Re: Area Of a Circle
« Reply #26 on: Sep 12th, 2007, 1:51am » |
Quote Modify
|
Here is an example of how differentiation can be useful, even though limits make no sense.
You may know that a polynomial f(x) has repeated roots (over 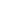 , say) if and only if f(x) and f'(x) have a common (non-constant) factor. That is, by applying polynomial division with remainder, you can perform the Euclidean algorithm to compute gcd(f, f'). If you get a constant, then f has distinct roots (f is separable).
But in fact, this result holds with polynomials over any field F, if we compute the derivative formally. That is, if f(x) =  akxk, define f'(x) = k akxk-1. The proof only uses that F is a field.
One reason this result is useful is that one can show certain fields F are "perfect", which means any irreducible polynomial over F has no repeated roots, or that any algebraic field extension of F is "separable", which is an important concept in field theory.
In fact, this is almost immediate if F has characteristic 0 (that is, it contains a copy of  ): if f is a non-constant polynomial, then f' is non-zero, and has smaller degree than f. If f is irreducible then, it can't have a common factor with f', and so f has distinct roots.
But suppose F=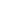 p is the finite field with p elements, also known as " mod p", or /(p) = {0,1,...,p-1}. Then there are non-constant polynomials whose derivative is 0. For example, if g(x)=xp-1, then g'(x) = pxp-1 = 0, even though g(x) is non-constant (even as a function on F). On the other hand, if h(x)=xp-x+1, say, then h(a)=1 for all a  F, so is "constant" in that sense, even though h'(x) = -1.
Now, since g'=0, g and g' share a common factor (namely g itself), so g has repeated roots. In fact, g(x) = xp-1 = (x-1)p. But if we were to view g as a polynomial over , it would be separable.
On the other hand, since h'(x)=-1, it is relatively prime to h, so h has no repeated roots over F.
The ability for f' to be 0 even when f is non-constant makes characteristic p fields more interesting. Finite fields are still perfect, but many infinite fields aren't.
Derivatives can be generalized even more, to any algebra A over a field F. An F-linear map d:A->A is called a derivation if d(uv)=d(u)v + ud(v). For example, if A=F[x], then d is uniquely determined by d(x); if d(x)=1, then d is the usual derivative. But in general, the set of all derivations on A is itself a vector space over F. This comes up in differential geometry, Lie algebras, and stuff. Ramble ramble.
|
|
IP Logged |
|
|
|
mikedagr8
Uberpuzzler
A rich man is one who is content; not wealthy.
Gender:
Posts: 1105
|
|
Re: Area Of a Circle
« Reply #27 on: Oct 23rd, 2007, 4:29am » |
Quote Modify
|
Officially started calculus, and have learnt a few things inc. limits as you guys said. And a few forms of the notation. Also the basics of derivatives.
|
|
IP Logged |
"It's not that I'm correct, it's that you're just not correct, and so; I am right." - M.P.E.
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print