 Author
Author |
Topic: (tanA)(tanB)(tanC) (Read 10022 times) |
|
ThudnBlunder
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
(tanA)(tanB)(tanC)
« on: May 17th, 2008, 12:09pm » |
 Quote Quote  Modify Modify
|
Prove that for any acute triangle (tanA)(tanB)(tanC) 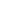 3 3 3 3
|
| « Last Edit: May 17th, 2008, 9:00pm by ThudnBlunder » |
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
Benny
Uberpuzzler
    

Gender: 
Posts: 1024
|
 |
Re: (tanA)(tanB)(tanC)
« Reply #1 on: May 17th, 2008, 12:40pm » |
 Quote Quote  Modify Modify
|
A+B+C = pi
C = pi - (A+B)
tanC = -tan(A+B)
tanC = -(tanA + tanB)/(1 - tanA tanB)
tanA + tanB + tanC
= tanA + tanB - (tanA + tanB)/(1 - tanA tanB)
= {tanA(1 - tanA tanB) + tanB(1 - tanA tanB) - tanA - tanB}/(1 - tanA tanB)
= {tanA - tanA*tanA*tanB + tanB - tanA*tanB*tanB - tanA - tanB}/(1 - tanA tanB)
= -tanA*tanB(tanA + tanB)/(1 - tanA tanB)
= tanA * tanB * tanC
So we have
tanA + tanB + tanC = tanA * tanB * tanC
or by dividing by tanA tanB tanC
cotB cotC + cotA cotC + cotA cotB = 1.
By squaring both sides of S = cotA + cotB + cotC we find
S^2 = (cotA)^2 + (cotB)^2 + (cotC)^2 + 2.
Now we know that
(cotA - cotB)^2 + (cotB - cotC)^2 + (cotC - cotA)^2 >= 0
and thus
2((cotA)^2 + (cotB)^2 + (cotC)^2)
- 2(cotB cotC + cotA cotC + cotA cotB) >=0
or
2(S^2 - 2) - 2 >= 0
2S^2 - 6 >= 0
S^2 - 3 >= 0
and we find that S>= sqrt(3) (as it must be positive), which is exactly what you were looking for.
|
|
 IP Logged IP Logged |
If we want to understand our world — or how to change it — we must first understand the rational choices that shape it.
|
|
|
ThudnBlunder
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Re: (tanA)(tanB)(tanC)
« Reply #2 on: May 17th, 2008, 1:07pm » |
 Quote Quote  Modify Modify
|
on May 17th, 2008, 12:40pm, BenVitale wrote:
So we have
tanA + tanB + tanC = tanA * tanB * tanC
<snipped>
and we find that S>= sqrt(3) (as it must be positive), which is exactly what you were looking for.
|
|
Looks good, except  3 is not exactly what I was looking for. That would be 3 3 is not exactly what I was looking for. That would be 3 3 3 
HINT:Once you have proved tanA + tanB + tanC = tanA * tanB * tanC you can use a well-known inequality for the rest.
|
| « Last Edit: May 17th, 2008, 1:16pm by ThudnBlunder » |
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
william wu
wu::riddles Administrator
    


Gender: 
Posts: 1291
|
 |
Re: (tanA)(tanB)(tanC)
« Reply #3 on: May 20th, 2008, 2:28pm » |
 Quote Quote  Modify Modify
|
For notational brevity, let a = tan A, b = tan B, and c = tan C.
Applying the AM-GM inequality yields
(a + b + c)/3  (abc)1/3. (abc)1/3.
As Ben showed, a b c = a + b + c in this case. Substituting this relation into the left hand side yields abc/3  (abc)1/3, which, after some algebra, yields abc >= 3 (abc)1/3, which, after some algebra, yields abc >= 3  {3}. {3}.
Hence, a + b + c = abc  3 3  {3}. {3}.
|
| « Last Edit: May 20th, 2008, 2:29pm by william wu » |
 IP Logged IP Logged |
[ wu ] : http://wuriddles.com / http://forums.wuriddles.com
|
|
|
l4z3r
Newbie


Posts: 10
|
 |
Re: (tanA)(tanB)(tanC)
« Reply #4 on: Aug 30th, 2008, 6:05am » |
 Quote Quote  Modify Modify
|
on May 17th, 2008, 1:07pm, ThudanBlunder wrote:
HINT:well-known inequality for the rest. |
|
Jensen's Inequality?
When A+B+C=n  then then  (tan A) = (tan A) = 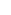 (tan A). (tan A).
Let f(x)=tan x. 0<x< /2 /2
The second differential of f(x) is always positive between o and  /2. Hence, the function is convex. (It would have sufficed if the graph of tan x was observed, actually). /2. Hence, the function is convex. (It would have sufficed if the graph of tan x was observed, actually).
Jensen's inequality gives us:
(tan A + tan B + tan C)/3  tan ((A+B+C)/3) tan ((A+B+C)/3)
A + B + C =  . .
Hence Proved  WOOT! WOOT!
my first solution on this site, i think.
|
|
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register