Author |
Topic: A Beastly Number (Read 1813 times) |
|
ThudnBlunder
Uberpuzzler
The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
A Beastly Number
« on: Nov 26th, 2008, 9:05am » |
 Quote  Modify
|
a) Find the first 6 digits of (10666)!
b) How many trailing zeros does the above number have?
|
| « Last Edit: Nov 26th, 2008, 1:12pm by ThudnBlunder » |
 IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: A Beastly Number
« Reply #1 on: Dec 2nd, 2008, 10:32am » |
Quote Modify
|
For an easier part b), I get: 2664(5667 - 1)
|
|
IP Logged |
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: A Beastly Number
« Reply #2 on: Dec 3rd, 2008, 12:31am » |
Quote Modify
|
According to the following article, solving part a) may require calculation of a certain logarithm to a precision of more than 670 decimal digits!
|
|
IP Logged |
|
|
|
ThudnBlunder
Uberpuzzler
The dewdrop slides into the shining Sea
Gender:
Posts: 4489
|
|
Re: A Beastly Number
« Reply #3 on: Dec 4th, 2008, 6:56pm » |
Quote Modify
|
on Dec 2nd, 2008, 10:32am, Barukh wrote:| For an easier part b), I get: 2664(5667 - 1) |
|
If we take n/4 as an estimate for the number of trailing zeros, we get 2.5*10665
Your number is 5 times this.
|
|
IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: A Beastly Number
« Reply #4 on: Dec 5th, 2008, 12:15pm » |
Quote Modify
|
on Dec 4th, 2008, 6:56pm, ThudanBlunder wrote:
Your number is 5 times this. |
|
Yes, I should've written 5666 instead. But now I realized the answer is incorrect anyway (doesn't take into account fractions).
To write the answer in a "compact form" may be as difficult as part a) then...
|
|
IP Logged |
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 2084
|
|
Re: A Beastly Number
« Reply #5 on: Dec 5th, 2008, 12:32pm » |
Quote Modify
|
2)   10666/5n
n=1
Where in practice the upper bound can be reduced to 666 log 10 / log 5 = 952
Edit:
|
= 26665666 / 4 +
| 286
n=1 |
2666/5n
|
Edit2: all of which I think I can safely assume anyone hanging around in Putnam already knew (and is clearly the driver for Barukh's answer), but since this thread has only seen a little action I thought I'd put it out there anyway. 
--SMQ
|
| « Last Edit: Dec 5th, 2008, 1:19pm by SMQ » |
IP Logged |
--SMQ
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: A Beastly Number
« Reply #6 on: Dec 6th, 2008, 9:52am » |
Quote Modify
|
SMQ, you are right. My answer is wrong, since it doesn't take into account the second term in your formula - the sum which is challenging to evaluate.
After working it out, I get the following answer to b): 26645666 - 143. 
I will supply details later, after I find the answer to the first question.
|
|
IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
|
Re: A Beastly Number
« Reply #7 on: Dec 6th, 2008, 12:25pm » |
Quote Modify
|
on Dec 6th, 2008, 9:52am, Barukh wrote:After working it out, I get the following answer to b): 26645666 - 143.
|
|
So is there a clever way to compute the sum of the digits of 2666 = 34004...233245?
Actually, the approximation 333*log5(2) is pretty good here.
|
|
IP Logged |
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
on Dec 6th, 2008, 12:25pm, Eigenray wrote:
So is there a clever way to compute the sum of the digits of 2666 = 34004...233245? |
|
I don't know. I used high-precision software (MPFR) to compute the number (I still want to get a confirmation it's correct).
Quote:| Actually, the approximation 333*log5(2) is pretty good here. |
|
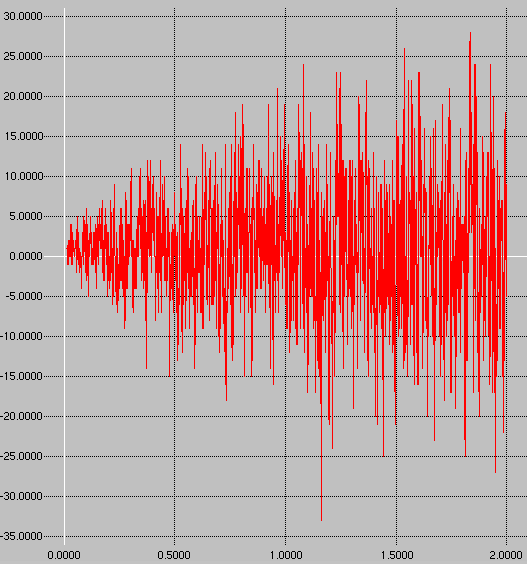
Yes, but it may be quite inaccurate for other exponents. In the attached graph, I plotted the discrepancies between your approximation and actual number for all cases 10n with 10 < n < 2000.
Again, if my calculations are correct.
|
|
IP Logged |
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: A Beastly Number
« Reply #9 on: Dec 7th, 2008, 11:21pm » |
Quote Modify
|
I get the following answer to part a):
13407273847...
|
|
IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
|
Re: A Beastly Number
« Reply #10 on: Dec 8th, 2008, 7:57am » |
Quote Modify
|
on Dec 7th, 2008, 11:21pm, Barukh wrote:I get the following answer to part a):
13407273847... |
|
Are you sure it's not 134072738469787? But the first 6 digits are correct 
And the 143 is correct, as the following short (but rather inefficient) program shows:
Code:
#include<stdio.h>
int A[300];
int main() {
int n,i,c;
A[0]=1;
for(n=0;n<666;n++) for(c=i=0;i<300;i++) {
c+=2*A[i];
A[i]=c%5;
c/=5;
}
for(c=i=0;i<300;i++) c+=A[i];
printf("%i\n",c/4);
} |
|
|
| « Last Edit: Dec 8th, 2008, 8:21am by Eigenray » |
IP Logged |
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: A Beastly Number
« Reply #11 on: Dec 8th, 2008, 10:19am » |
Quote Modify
|
on Dec 8th, 2008, 7:57am, Eigenray wrote:
Are you sure it's not 134072738469787?
|
|
Hmm... I did calculate the logarithm with very high precision, so at least 15 digits should be accurate. Then, I did exponentiation with a double precision. Could it be I lost 5 digits of accuracy there? 
What's your method?
|
|
IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
|
Re: A Beastly Number
« Reply #12 on: Dec 8th, 2008, 12:44pm » |
Quote Modify
|
Code:
In[1]:= u=1-FractionalPart[ N[10^666 Log[10,E], 686] ]
Out[1]= 0.72825054586682085824
In[2]:= v=N[Log[10,Sqrt[2 Pi]], 20]
Out[2]= 0.39908993417905752478
In[3]:= 10^(u+v)
Out[3]= 13.407273846978712508
|
|
What do you get?
Edit: And here it is with MPFR:
Code:#include<stdlib.h>
#include<stdio.h>
#include<gmp.h>
#include<mpfr.h>
int main() {
mpfr_t u,v;
mpfr_set_default_prec(10000);
mpfr_init_set_ui(v,10,GMP_RNDN);
mpfr_pow_ui(v,v,666,GMP_RNDN); //v=10^666
mpfr_init_set_ui(u,1,GMP_RNDN);
mpfr_exp(u,u,GMP_RNDN);
mpfr_log10(u,u,GMP_RNDN); //u=log_10 e
mpfr_mul(u,u,v,GMP_RNDN);
mpfr_frac(u,u,GMP_RNDN); //u=frac[10^666 log_10 e]
mpfr_set_si(v,-1,GMP_RNDN);
mpfr_acos(v,v,GMP_RNDN);
mpfr_mul_ui(v,v,2,GMP_RNDN); //v=2pi
mpfr_log10(v,v,GMP_RNDN);
mpfr_div_ui(v,v,2,GMP_RNDN); //v=log(sqrt(2pi))
mpfr_sub(v,v,u,GMP_RNDN);
mpfr_ui_pow(v,10,v,GMP_RNDN); //10^(v-u)
mpfr_out_str(stdout,10,20,v,GMP_RNDN);
printf("\n");
} |
|
Gives 1.3407273846978712508
(I already had GMP but apparently it doesn't do logs. So I downloaded the MPFR sources and started ./configure; make. Then I realized I could install it through Cygwin, and wrote the above before it finished compiling.)
|
| « Last Edit: Dec 8th, 2008, 2:00pm by Eigenray » |
IP Logged |
|
|
|
ThudnBlunder
Uberpuzzler
The dewdrop slides into the shining Sea
Gender:
Posts: 4489
|
|
Re: A Beastly Number
« Reply #13 on: Dec 9th, 2008, 4:03pm » |
Quote Modify
|
My source for this problem got yet a different answer, 1.340727397...
|
| « Last Edit: Dec 9th, 2008, 4:06pm by ThudnBlunder » |
IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
|
Re: A Beastly Number
« Reply #14 on: Dec 9th, 2008, 5:32pm » |
Quote Modify
|
The funny thing is that he did compute the fractional part of 10666/log(10) correctly to 14 digits. But he decided to round it to 8 digits before exponentiating, and then claim 10 digits of accuracy in the result:
Quote: {2 } x 10-0.27174945 = 1.340727397, |
|
which is silly.
|
|
IP Logged |
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print