 Author
Author |
Topic: Combinatorial Sum (Read 1611 times) |
|
ThudnBlunder
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Combinatorial Sum
« on: Jan 20th, 2009, 5:09am » |
 Quote Quote  Modify Modify
|
49
Evaluate  (-1)k (-1)k  99 99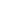 2k 2k = =  99 99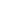 0 0 - -  99 99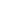 2 2 + +  99 99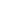 4 4 - ....... - - ....... -  99 99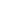 98 98
k=0
|
|
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: Combinatorial Sum
« Reply #1 on: Jan 20th, 2009, 7:50am » |
 Quote Quote  Modify Modify
|
1/2 sumn=0..99 C(99, n) in 1(99-n) + 1/2 sumn=0..99 C(99, n) (-i)n 1(99-n)
((1+i)99+(1-i)99)/2
[sqrt(2)99 exp(99 * 2pi * 1/8 i) + sqrt(2)99 exp(99 * 2pi * 7/8 i)]/2
248.5 [exp(6*pi/8 i) + exp(10*pi/8 i)]
248.5 * -sqrt(2)
-249
|
| « Last Edit: Jan 20th, 2009, 7:52am by towr » |
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
pex
Uberpuzzler
    

Gender: 
Posts: 880
|
 |
Re: Combinatorial Sum
« Reply #2 on: Jan 20th, 2009, 8:45am » |
 Quote Quote  Modify Modify
|
So, more generally, sumk=0..floor(n/2) (-1)k nC2k =| hidden: | 2n/2 ......... if n = 0 mod 8
2(n-1)/2 ... if n = +- 1 mod 8
0 ............. if n = +- 2 mod 8
- 2(n-1)/2 ... if n = +- 3 mod 8
- 2n/2 ........ if n = 4 mod 8. |
Interesting!
|
|
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register