FRACTALS
an introduction to fractals. topics discussed include fractals in nature and industry, and the basic mathematics behind generating several classic structures, including the mandelbrot set and sierpinski triangle. also included is a gallery of choice fractal art, including a few pieces made by myself.
|
 |
|
|
|
A Short And Entertaining Introduction to Fractals

|
|
a fractal is a geometric shape that can subdivided into parts, each of which is a reduced-size copy of the whole. the term was coined in the 1960s by benoit mandelbrot, a mathematician at IBM who adapted it from the latin adjective fractus, meaning "fragmented." to get a feel for what a fractal is, imagine inspecting a long, craggly, leafless tree branch on a frosty winter day. as your eyes scan the branch from its base to its tips, you notice that many sub-branches are generated along the way, and each sub-branch has a structure symmetric to the original, but smaller in scale. these sub-branches in turn fork off self-symmetric branches of their own. in the purest sense of a fractal, we imagine this branching process as never ending. you could compare it to the effect produced when two mirrors are faced toward each other, producing a claustrophobic, tunnel-like view of infinite imitation at smaller and smaller scales. a nice example of this is seen in the mandelbrot fractal at left, designed by Paul deCelle.
|
|
|
|
usually one's first response to fractals is simply this: they are beautiful! indeed, they are visually arresting, and there are many reasons why. perhaps one reason is that they exhibit extreme levels of symmetry, a property we have gravitated toward throughout human history, whether it be in our architectural designs, in our scientific theories, in our religions, or even in the facial structures of the opposite sex. another reason could be that the same self-replicative patterns can be found strewn throughout our natural universe, in vapor trails, snail shells, evergreens, cauliflowers, and snowflakes ... just to name a few. but perhaps most enticing is a reason most people would never guess -- mathematical brevity. many of these stunning patterns are governed by very simple-looking equations consisting of only a few symbols! it is impressive that just a few lines of math can so well capture such intricate aspects of our natural world. the philosophical implications of this are fun to think about. in accordance with occam's razor, does this suggest that nature truly prefers simplicity? or as mathematician stephen wolfram conjectures, could the underlying rules of the universe be governed by just three or four lines of code?
|
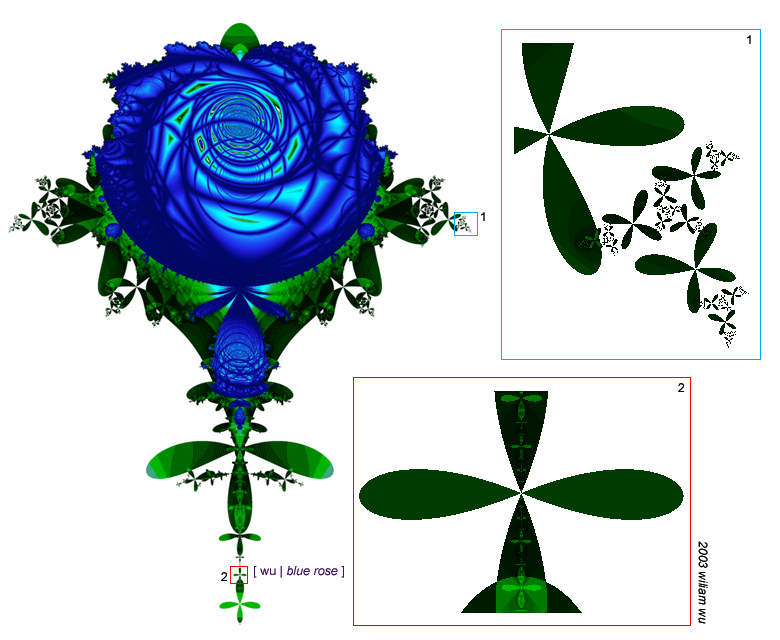
with so much intrinsic beauty, it isn't surprising that fractals now have their own artistic genre. powerful modern-day computers and graphics software have allowed everyday people to easily generate breathtaking high-detail fractals and embellish them with their own designs. the skeletal shape of a fractal is concocted with recursive equations, mixing various kinds of functions and parameters. afterwards, they apply whatever creative tweaks they can imagine, such as coloring schemes, lighting effects, or even superimposing several layers of fractals together! as an example, to the left is a piece i made, in which i contorted a mandelbrot fractal into the shape of a blue rose. self-symmetries can be found throughout the rose, particularly at the rose's center, at the petal rims, and in the green leaves, as the zoom-ins illustrate.
|
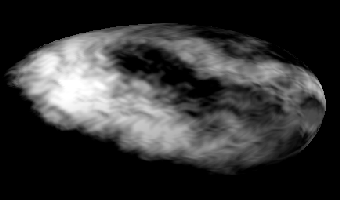 |
aside from just being attractive and confusing, fractals also have many practical applications due to their elegant connections with the natural world. they can be used by mapmakers to measure the lengths of coastlines, and by aeronautical engineers to simulate turbulence. they are involved in the construction of scalable fonts -- fonts that can be enlarged or shrunk while still preserving the aesthetic properties of brush written characters, such as those found in chinese calligraphy. and they are often used to produce snazzy computer graphics effects, such as the digital cloud to the left.
|
|
fractals can even be used to make music! if you think of music as a sequence of amplitudes values over time, one could imagine constructing a sequence such that its amplitudes result from the repeated application of some algorithm to previous amplitude values, thereby exhibiting the self-similarity property of fractals. the results are rather interesting. for an example of fractal music, click on the musical notes to the right. believe it or not, you're listening to the difference equation x[n+1] = x[n]*b*(1-x[n]), as manipulated by artist Martin Guertner. the value x[n] is mapped to various musical parameters such as pitch and duration.
|
 |
this concludes my introductory comments about fractals. i hope you now have a general idea of what a fractal is, why they are fascinating, and how they are being used today.
the rest of the site is devoted to two objectives. the first is: 1) to showcase sexy fractals, which is something i'm sure everyone can appreciate! to meet this objective, i point you to the fractal gallery, a collection of art pieces that i find quite nice. most of them are by Paul deCelle, who kindly let me show some of his great work on this site. the gallery also contains some pieces by me that i'm proud of, in my own amateurish way.
the second objective is: 2) to clearly explain the basic mathematics governing some standard fractals, such as the Mandelbrot and Julia sets, the Sierpinski triangle, and the Lorenz attractor. while it is easy to see how fractals exhibit self-symmetry and resemblances to natural phenomena, some explanation is needed to see how tiny equations can generate such awesome images. the math is actually not complicated at all, and i hope it will come across this way. this is still work in progress; even the existing pages on the mandelbrot and sierpinski fractals need to be completely redone.
 |
| W. Wu, 2000-2005 ©. |
|