| computer science |
| ROTATED SORTED LIST SEARCH |
An element in a sorted array can be found in O(log n) time via binary search. But suppose I rotate the sorted array at some pivot unknown to you beforehand. So for instance, 1 2 3 4 5 might become 3 4 5 1 2. Now devise a way to find an element in the rotated array in O(log n) time.
|
| ASCII TO INT |
int atoi(char* pStr)
Write the definition for the atoi (ASCII to integer) function without using any built-in functions. If pStr is null, return 0. If pStr contains non-numeric characters, either return 0 (ok) or return the number derived so far (better) (e.g. if its "123A", then return 123). Assume all numbers are positive. Plus or minus signs can be considered non-numeric characters.
|
| LINKED LIST LOOP |
Using a constant amount of memory, find a loop in a singly-linked list in O(n) time. You cannot modify the list in any way.
Note: "Constant memory" = the memory required for the solution cannot be a function of n.
|
| PALINDROME TEST |
Write a little program that accepts as input a string, and outputs a boolean value telling whether or not the input is a palindrome. (As always, there are both smart and stupid ways to do this ...)
|
| REPEATED NUMBER |
You are given a sequence S of numbers whose values range from 1 to n-1. One of these numbers repeats itself once in the sequence. (Examples: {1 2 3 4 5 6 3}, {4 2 1 2 3 6 5}). Write a program that finds this repeating number using a constant amount of memory. Now what if there are two repeating numbers (and the same memory constraint)?
Note: "Constant memory" = the memory required for the solution cannot be a function of n.
|
| XOR FROM NAND |
Make an XOR gate using only NAND gates.
|
| QUICKSORT |
Write quicksort.
|
| MALLOC |
Implement malloc.
|
| STRING PERMUTATIONS |
Write a function to print all of the permutations of a string.
|
I/O COMPLETION PORTS
>=P |
I/O completion ports are communications ports which take handles to files, sockets, or any other I/O. When a Read or Write is submitted to them, they cache the data (if necessary), and attempt to take the request to completion. Upon error or completion, they call a user-supplied function to let the users application know that that particular request has completed. They work asynchronously, and can process an unlimited number of simultaneous requests. Design the implementation and thread models for I/O completion ports. Remember to take into account multi-processor machines.
Note: Argh, I should know how to do this after taking CS162.
|
| BINARY TREE PRINT |
How would you print out the data in a binary tree, level by level, starting at the top?
|
| BASE N |
Demonstrate addition in some base n, where n is not 2, 8, 10, or 16. Now try n = -2.
|
| STRING REVERSAL |
Reverse the words in a sentence, i.e. "My name is Chris" becomes "Chris is name My." Optimize for speed. Optimize for space.
|
| STORAGE ALGORITHM |
Given that you are receiving samples from an instrument at a constant rate, and you have constant storage space, how would you design a storage algorithm that would allow you to get a representative readout of data, no matter when you looked at it? In other words, representative of the behavior of the system to date.
Update: Got several dozens of answers for this one, thanks /.
|
| SORTING ALGO COMPARISON |
Describe the various standard sorting algorithms (the ones you learned in school), and discuss advantages and disadvantages. When would you use one over another; why?
|
| MULTIPLY WITHOUT MULTIPLYING |
Multiply by 8 without using multiplication or addition. Now do the same with 7.
|
| STRING COMPARISON |
Compare two strings using O(n) time with constant space.
|
| LINKED LIST VS. ARRAY |
What's the difference between a linked list and an array?
|
| DYNAMIC PROGRAMMING |
A burglar breaks into an electronics store. He has a bag of volume V, and he sees N different gadgets, each with its own price value. He wants to choose gadgets that maximize the value of his steal, while maintaining his volume constraint. Write a dynamic programming algorithm that calculates which objects should be chosen, and the value of the optimal steal.
|
| SUBSTRING SEARCH |
Given two strings A and B, write a program that determines if A is a substring of B. Optimize for speed. Optimize for space.
|
| STRING INTERSECTION |
Given two strings A and B, write a program that returns the intersection of A and B (could be null). Now speed it up. Now test it.
|
| NUMBER SPIRAL |
Write a program that will display a "spiral" of NxN numbers, using constant space (no arrays allowed). For example, here's what the spiral looks like for N=10:
99 98 97 96 95 94 93 92 91 90
64 63 62 61 60 59 58 57 56 89
65 36 35 34 33 32 31 30 55 88
66 37 16 15 14 13 12 29 54 87
67 38 17 4 3 2 11 28 53 86
68 39 18 5 0 1 10 27 52 85
69 40 19 6 7 8 9 26 51 84
70 41 20 21 22 23 24 25 50 83
71 42 43 44 45 46 47 48 49 82
72 73 74 75 76 77 78 79 80 81
Note: many thanks to hordes of /.'ers for pointing out an error in the readout
|
| ONES IN A REGISTER |
How can you determine the number of ones in an n-bit register only using i iterations, where i is the number of ones in the register?
Update 7/24/2002 2:58AM: Received many solutions for this problem now thanks to /. I promise to eventually credit all the people who sent me stuff.
|
| REGISTER VALUE SWAP |
In constant time, without using any extra memory, exchange the values of two equally sized variables (e.g. 32 Bit Ints,
but infinitely long also works, giving it a more theoretical touch).
|
| VARIABLE RENAMER |
You are writing a parser that reads a C program and translates all the variable names into new names of the form "VAR######", where ###### is an integer incremented for each unique variable name. Discuss what is needed for the case where the C program already contains a variable of the form "VAR######".
|
| ROBOT COLLISION PROGRAMMING |
Two robots are to be parachuted onto random locations on an infinite line. When they land, their parachutes detach and remain where they are. The robots may be programmed from the following instruction set:
- Go left one unit
- Go right one unit
- Skip next instruction unless there is a parachute here
- Go to label
Each instruction takes one cycle to execute. Program the robots to collide.
Note: From Microsoft. How cool!
|
| ADD ONE WITHOUT USING + OR - |
Write a C/C++ program that takes an unsigned integer and adds 1 to it without using the plus or minus signs. Don't worry about overflow issues. It is cheating to use assembly commands, or to write a preprocessor that uses ASCII codes to insert the plus or minus sign. There are many solutions, some more elegant than others.
Note: From Atari Games!
|
| ARRAY ROTATION |
You are given an array with n elements { x1, x2 ... xk ... xn }. You are also given an array location k.
Using constant space and O(n) time, rotate the array such that it contains { xk, xk+1 ... xn, x1, x2 ... xk-1 }.
|
| DATING POSSIBILITIES |
E is a set of boys and girls. P is a set of unordered pairs (x,y) of those boys and girls. If two people are in a pair, then they would be willing to go on a romantic date. List out all the possible dating combinations that could occur in one night, such that no person dates more than one other person that night. (Technically: Generate all subsets of P such that no person is used more than once per subset.)
Example:
E = { Alice, Bob, Cole, Doris }
P = { (Alice,Bob) (Alice,Cole) (Bob,Doris) (Cole,Doris) }
A maximal number of dating scenarios that could occur in one night, such that no one dates more than one person in the same night:
{(Alice,Bob)}
{(Alice,Cole)}
{(Bob,Doris)}
{(Cole,Doris)}
{(Alice,Bob),(Cole,Doris)}
{(Alice,Cole),(Bob,Doris)}
|
| FOR LOOP TWEAKS |
How well do you know C "for" loops?
Find three ways to make the program below to print 20 copies of the dash character '-' by changing/adding only one character:
int i, n=20;
for (i=0; i < n; i--) {printf("-");};
|
| NTH FROM END |
Find the nth element from the end of a linked list (where n < size of list).
Note: asked at m$ interviews.
|
| TRIANGLE INTERIOR |
I give you three points on a Cartesian plane which define the vertices of a triangle. Now I give you a fourth point. Write up an algorithm that can determine if the fourth point is within the interior of the given triangle.
Note: From topcoder.com via Yosen Lin. Topcoder is an online competition arena where people try to code correct solutions to problems as quickly as possible, for prize money. Speed is a big deal. If you're writing a nasty solution for this problem that involves solving several simultaneous equations, you're taking the standard route. There is a more clever way that is very snappy and elegant.
|
| OBFUSCATED PI |
Explain exactly how this code works. Particularly, every character in the first three lines.
#define _ F-->00 || F-OO--;
long F=00,OO=00;
main(){F_OO();printf("%1.3f\n", 4.*-F/OO/OO);}F_OO()
{
_-_-_-_
_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_
_-_-_-_
}
Note: From the Obfuscated C code contest. Click here for more wacky 1337 code.
|
| PUNCHOUT CARDS |
You have a box and N cards. Each card is blue on one side, white on the other. Because of the asymmetric shapes of the cards, which exactly match the shape of the hole in the box, each card will fit in the box in only two possible ways (gray-side-up or white-side-up). Each card contains 2R circles lined up in two columns and R rows, each of which may be punched out (so it is a hole) or not. Your puzzle is to see if you can place all the cards in the box (each one either gray-side-up or white-side-up) so as to completely cover the bottom of the box, i.e. each of the 2R circle positions is covered by at least one card that has no hole punched out there.
Example: In the cards for Puzzle 1 (left example below), with 2 cards each with 2 rows, it is not possible to put them in the box to cover each circle, but with Puzzle 2 (right example below), with 2 cards each with 3 rows, it is possible. (Punched-out-circles are shown in black).
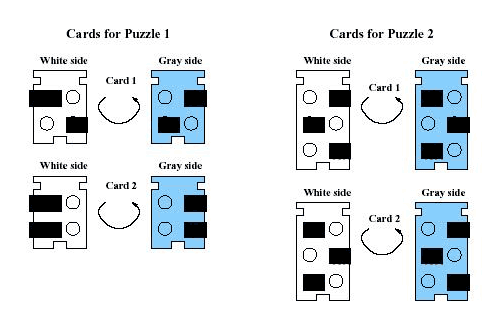
Show that this problem (deciding if the cards can be put in the box to cover each circle position) is NP-complete.
|
| STEINER TREE |
INSTANCE: G = (V,E) is an undirected graph. R is a subset of vertices V. k is a positive integer.
QUESTION: Does there exist a subtree of G that includes all vertices of R and contains at most k edges?
Example: The graph G below, with R = { 1, 2, 3, 4, 5, 6, 10 } and k = 8, is a "yes" instance.
Prove that this problem is NP-complete.
|
| P ?= NP |
Suppose next week someone announced and provides a conclusive proof that P != NP. In a paragraph, explain what impact you believe such a result would have on the field of computer science and on society at large.
(alternatively) Suppose next week someone announced and provides a conclusive proof that P = NP. In a paragraph, explain what impact you believe such a result would have on the field of computer science and on society at large.
Note: Part a. was an extra credit problem on the CS172 Spring 2001 Final Exam at UC Berkeley.
|
| NONCONSTRUCTIVE P = NP |
You've made the breakthrough every theorist dreams of: you've solved P vs NP. Surprisingly enough, you've shown that P=NP, but sadly your proof was non-constructive. Design a poly-time program to solve SAT.
|
| KNIGHT TOURS |
-
For a chessboard of standard 8X8 size, write a program devise a path for a Knight using standard Knight moves to visit all squares once and only once. The square the Knight starts on is counted as visited.
(FYI, a knight can move following this rule: 2 squares across and 1 square down or 2 squares down and 1 square across.)
- NO BRUTE FORCE approaches. Optimize code for speed.
- Do not hard code the starting square. Make it a parameter.
If that is too easy, here is another restriction: The problem described above is known as a Knights Tour. You can modify your code to do a Complete Knights Tour, where the final square visited by the Knight is directly adjacent (not diagonal) to the square the Knight started on.
If you think all of that is too easy, use recursion.
|
| SUPER-VILLAIN TRANSPARENCIES |
You're a super-villain and you want to prepare a transparency (the kind that goes on an overhead projector) with the key points of your plan for world domination so you can present them to the hero/superagent before you attempt to kill him in some ridiculously novel way. You don't want this information to fall into the wrong hands before you're ready. Smart villain that you are, you know you can share the information across several slides so that if the enemy agents capture any 2 of your slides, they won't learn even the tiniest bit of information about your plan. How?
Note: Awfully cool riddle, isn't it :) Thanks to Alex Harris.
|
| BST TO LL |
You are given a binary search tree with nodes of the following form:
struct node {
struct node *left;
struct node *right;
}
Write a simple function that converts the tree to an ordered doubly linked list by changing the links in the existing tree. Your function should have the following form:
void bst2ll(struct node *root, struct node *first, struct node *last);
where first and last are return values.
|
| THREE INVERTERS FROM TWO |
Construct a circuit which takes three binary inputs, a, b, c, and creates as outputs their complements, a', b', c', (NOT a, NOT b, NOT c) with the restriction that you may only use two inverters (NOT gates), and all the AND gates and OR gates that you wish.
Now generalize. How many inverters do you need to compute the complements of N inputs?
|
| LONGEST TERMINATING PROGRAM |
Given a computer with 8k bytes of memory (RAM), and an execution speed of 1 billion (10**9) instructions per second, what is the longest terminating program (in terms of execution time) which can run on the machine? "Terminating" means that the program is guaranteed to execute some HALT instruction.
The desired solution is simply a "back of the envelope" estimate. The exact answer, of course, depends on details such as exactly what the instruction set looks like, and so forth. Feel free to make reasonable assumptions, where necessary.
|
| 2-SAT TO 2-COL |
Reduce 2-SAT to 2-COLORABILITY.
|
| SINGLE-INSTRUCTION COMPUTER |
Consider the Single Instruction Computer (SIC). It has only one operation, and no registers, taking everything from memory. The only operation is called sbn, for Subtract and Branch if Negative. It takes three operands, all of which are memory addresses. It works like this:
- Take the instruction sbn a, b, c.
- Let the value at address a equal the value at address a minus the value at address b.
(In C language, that would be *a = *a - *b;)
- If new value at a is less than 0, jump to memory address c and do instructions from there. Else go to next instruction.
(c is usually interpreted as a label.)
Despite its tininess, this instruction set is still capable of doing many things, perhaps more than you would expect.
| EASY |
Implement left shift. Given an address a, shift the value in a one bit to the left. Bring in zeroes on the right. (Hint: Remember that left shift is the same as multiply by two...now...how can we do that...?)
Implement unconditional jump. Make an unconditional jump, that will always jump to to the label at c. Use a temporary variable. (Big Hint: This takes me two instructions. Here's my answer: sbn temp, temp ; sbn temp, one, LABEL.)
Implement multiplication. Given two addresses, a and b, set another address c equal to a times b. Assume that the values of a and b are nonnegative, and you can change them. Work on figuring out how to do a loop, too. (Then, do it so that you can't assume they're nonnegative, and do it without changing them. That's a bit harder.)
Implement sign checking. Given an address a, set another address b to equal true if the value in a is negative, or set b to false if it is nonnegative. You might want to take this opportunity to find good values to represent true and false with. (Hint: This will come in handy in some of the rotate and shift commands...do you know why?)
|
| MEDIUM |
Implement compare-to-zero. Given an address a, set another address b to equal true if the value at a is equal to 0, and false if the value at a is not equal to 0. Do not change the value in a.
Implement left rotate. Given an address a, rotate it one bit to the left, bringing in the bit from the left on the right side.
|
| HARD |
Implement right rotate. Given an address a, rotate the value in the address a one bit to the right, bringing in the bit from the right on the left side.
|
Note 1: Assume that values at the addresses are standard 8-bit signed integers in two's complement form. You can also assume there is an address called ONE that always starts out with the value one. Use ONE to make incrementation and decrementation easier, and for making boolean values. Also you can use the notation .+1 to show that c equals the next instruction's address, so that even if a < 0, the program goes to the next instruction anyway, as in sbn a, b, .+1
Note 2: To help you get started, here's how you would implement addition:
sbn temp, temp
sbn temp, b
sbn a, temp
// Line-by-line explanation:
Line 1: Since we don't know what was in temp before, it's uninitialized. But doing this will initialize it and set it to zero, since temp - temp = 0. c is blank, so program flow will always go to the next instruction.
Line 2: temp = temp - b; since temp is zero, temp is now equal to -b. Since c is empty, even if -b is less than 0, program flow still goes to the next instruction
Line 3: a = a - temp; since temp = -b, this is a - (-b), which is a + b
Note 3: From the textbook "Computer Organization and Design: The Hardware/Software Interface" 2nd edition, by David A. Patterson and John L. Henessey, Morgan Kaufmann Publishers, San Francisco, California.
Note 4: What other operations can you think of that would make good puzzles? E-mail wwu at ocf.berkeley.edu.
|
| MISSING INTEGER IN ARRAY |
You have a 99 cell array. In each cell you put an integer belonging to the set {1,2,...,100}. No two cells contain the same integer. Thus when the array filling is complete, one of the integers from 1 to 100 is not present in the array. Determine which integer is missing from the array. (The lower the running time of your algorithm, the better.)
|
| HAL 9000 SHUTDOWN |
Aboard the spaceship Discovery, the HAL 9000 has gone rogue and needs to be shut down as quickly as possible! The computer has M microprocessors working in parallel, each of which is located in a different area of the ship. If any N of these processors is destroyed, the HAL 9000 will become inoperational. Using your trusty hammer, you plan to do exactly that. You have a map of the spaceship, which looks like a K by K maze grid with walls here and there. Coordinates (1,1) correspond to the corner square on the bottom-left of the map. The map shows the locations of all M processors. You are currently standing at coordinates (X,Y).
Having taken CS courses before, you realize that a computer program could help you out here. Although the on-board computers can't be trusted, you have an uncorrupted PDA that could do the job. Write an algorithm for finding the shortest route from where you are standing right now that allow you to bash N processors along the way. Assume that you can only move up, down, left, and right.
Note 1: All aforementioned variables are positive integers. M >= N. K >= X. K >= Y.
Note 2: Problem adapted from topcoder.com. Storyline by me =)
|
| EXCEL SIMULATOR |
Write a function which converts a number into an Excel spreadsheet column name.
0 = A
...
25 = Z
26 = AA
...
701 = ZZ
702 = AAA
Note: [from Misha Kruk] This one is easy, but a little bit tricky (in the "I guarantee that your first solution will fail" way).
|
| PERFECT POWERS |
Write a fast program that prints perfect powers (integers of the form mn, with m, n > 1) in increasing numerical order. So the first few outputs should be 4, 8, 9, 16, 25, 27, 32, ...
"Fast" is intentionally fuzzy. The original contest rules were that the programs had to be in a standard dialect of Basic and fit on one page, and the contest organizers would type them in and time them on their system, with the winner being the fastest one to print all perfect powers less than N = 10,000,000. A different rule might be that your algorithm has to work for unlimited N, and the algorithm that has the least time complexity (in the O(f(N)) sense) wins. Can you think of an algorithm that would win under the original rules but would be disqualified under the later rules?
Note: From a 1977 high school programming contest (Tim Mann).
|
| SELF-PRINTING PROGRAM |
Write a program that prints itself!
|
| PEG SOLITAIRE |
(Using topcoder.com problem statement format. You have an 8 second program execution limit on a 700 MHz Pentium III.)
PROBLEM STATEMENT
In the game of Peg Solitaire, you are given a arrangement of pegs that fit into a line of equally-spaced holes. In order to win the game, you must reduce the number of pegs to one, by using a series of jumps. Each jump occurs according to the following rules:
- A peg may only jump over those immediately adjacent to it on the left or right.
- A jumping peg must jump exactly one other peg, no more, no less.
- Once the jump is completed, the peg that was jumped over is removed.
For example, given the configuration of pegs and holes
...1234.5....
where a period represents an empty hole, and where a digit represents a peg, the only two legal moves are as follows:
...12..35.... [peg 3 jumped over peg 4, which was then removed]
..2..34.5.... [peg 2 jumped over peg 1, which was then removed]
A position is defined as "winnable" if, through a series of jumps, it can be reduced to one peg. For example, the above position is winnable, since it can be reduced to one peg by the following set of jumps:
...1234.5.... [initial]
...12..35.... [peg 3 jumped over peg 4]
.....1.35.... [peg 1 jumped over peg 2]
.....15...... [peg 5 jumped over peg 3]
....5........ [peg 5 jumped over peg 1]
Given a number N of pegs, write a method that returns the number of winnable positions that consist of N pegs.
NOTES
- When considering whether two positions are identical, disregard excess empty holes on the left and right side.
- Note that there is no "edge" of the playing field; there are essentially infinitely many empty holes.
- An input is valid if the following criterion is met: size will be an integer between 2 and 35, inclusive
TEST CASES
Input: 2
Output: 1
There is only one winnable case with 2 pegs; when they are adjacent.
Input: 4
Output: 3
The patterns containing 4 pegs are:
..12.3.4..
..12..34..
..1.2.34..
Input: 8
Output: 23
Note: A problem set from topcoder.com, written by Matt Lahut.
|
| MAXIMAL SUM IN INTEGER ARRAY |
Consider an array of integers a[1] ... a[n]. Design an O(n) algorithm that finds the pair I,J (with I <= J) such that the sum
is maximized. (Note that integers can be both positive and negative.)
Note: Source - UCB CS170 (Algorithms) Spring 2002, Homework 1.
|
| SECOND SMALLEST |
Find the second smallest integer in an array of n integers. Runtime restraint: n + O(log n) comparisons. Tricky!
Note: Source - UCB CS170 (Algorithms) Spring 2003, Homework 1.
|
| DFA DESIGN I |
1/31/2003 1:38AM
Imagine a world where multiplication over the symbols a, b, and c is defined as follows:
a b c
------------------------------
a | a a c
b | c a b
c | b c a
(interpret this table as saying a*a = a, b*c = b, and so on)
Given a string S = "s1s2 ... sn" composed of symbols a, b, and c, define the LR-Product of S as follows:
LR-Product(S) = ( ... (((s1 * s2) * s3) * s4) ... )
This essentially says multiply the first two digits, then take that product and multiply it by the third digit, then take [i]that[/i] product and multiply it by the fourth digit, and so on, processing the string in this fashion from left to right. Similarly, define the RL-Product of S as follows
RL-Product(S) = ( ... (((sn-1 * sn) * sn-2) * sn-3) ... )
This does the same thing, but moving from right to left.
Problem: Design a deterministic finite automaton (finite state machine) that accepts all strings
over the alphabet {a,b,c} whose LR-Product and RL-Product are identical.
Note 1: From Ranjit Jhala, GSI for CS172 (Computability and Complexity) at UCB, and my former CS170 GSI. Taken from discussion 1/29/2003.
Note 2: Note that the desired language is not quite a language of palindromes. There is no DFA which can accept palindromes.
Note 3: If you are unfamiliar with the terminology, feel free to ask. Or you can google search for lecture notes.
|
| BITONIC TOURS |
1/31/2003 1:38AM
The euclidean traveling-salesman problem is the problem of determining the shortest closed tour that connects a given set of n points in the plane. Figure (a) shows the solution to a 7-point problem.
In this problem, we consider a variation, the bitonic euclidean traveling-salesman problem. We consider only bitonic tours, that is, tours that start at the leftmost point, go strictly left to right to the rightmost point, and then go strictly right to left back to the starting point.
Describe an O(n2)-time dynamic programming algorithm for determining an optimal bitonic tour. You may
assume that no two points have the same x-coordinate. A full solution should include the following:
- Specify the dimensions of the data structure used in your DP algorithm, and explain how to retrieve the answer after the structure is filled.
- Specify which entries can be filled from the start (base case), and give a recursive formula for acquiring the other entries.
- Estimate the time needed to fill one entry, and give the total time needed to fill the whole matrix and find the answer to the problem.
Hint: What you need to do is divide
each point into two groups. We traverse the first group in left-to-right order, followed by
the second group in right-to-left order. There's an obvious algorithm which just tries every
possibility, but it is exponential. We'd like a dynamic programming solution that solves
subproblems from left to right, dealing with just the first i points in each case.)
Note: Source - UC Berkeley CS170 (algorithms), Spring 2002. Classmates and I stared at it forever in office hours.
|
| RegEx: ab, ba |
Write a regular expression (or equivalently, construct a deterministic finite automaton) that accepts strings over the alphabet { a, b } in which the number of occurrences of 'ab' = number of occurrences of 'ba'.
Note 1: What's a regular expression? Basically, it matches character strings that fit a certain pattern. You are restricted to the operators OR, CONCATENATE, and Kleene Star. And you can use all the parentheses you want. google(regular+expressions)
Note 2: This problem often trips people up because regular expressions are not supposed to have unbounded counting ability. There's a one-to-one correspondence between a regular expression and finite state machines, and the ability to count arbitrarily high requires an unbounded amount of state space. It follows that you cannot make a regular expression that matches all 0-1 strings of the form 0n1n, where n is an integer, and the notation 0n refers to the string of n consecutive zeroes. However, in this case there's something slightly cunning you can observe which will allow you to realize a Regular Expression.
|
| RegEx: half(L) |
A very hard problem. Let L be a regular language. Show that the following language is regular.
half(L) = { x : there exists a y such that xy is in L, and |x| = |y|}
Hint 1: It will be probably be too difficult to construct a RegEx for this. Try making a nondeterministic finite automaton. If you're not aware of it, there's a one-to-one correspondence between deterministic finite automata (DFA), and nondeterministic finite automata (NFA). This is surprising because one would expect nondeterminism to give us much added power, but it ends up being no better than a DFA.
Hint 2: Think about cross products. If you've ever seen the product construction based proof that regular languages are closed under intersection, that style of approach should be helpful for this problem.
|
| RegEx: divisible by 3 |
Construct a finite state machine (or equivalently, write a regular expression) which accepts all strings over the alphabet {0,1} which are divisible by 3 when interpreted in binary.
Note 1: There is a one-to-one correspondence between Regular Expressions and Finite State Machines. If you think you can solve the problem more easily by writing a regular expression, go ahead. However, a state machine approach will probably be more intuitive, and the solution will be more understandable.
Note 2: When scanned from left to right, the string is interpreted as moving from most significant bit to least significant, as expected.
|
| STACK INDEXING |
You are given a computer that can compile and execute C programs. Write a program in C to determine if the heap grows down and the stack grows up on this machine, or vice versa.
Note: From an Amazon.com interview.
|
| SWEETHEART MIX TAPE |
4/7/2003 12:17AM
Willywutang is organizing a mix tape for his overseas sweetheart, April Underwood. The tape will have her top N songs of all time. Willy was going to determine the order of these songs on his own, but then April found out about his little project. Being an obnoxiously demanding woman, she has now given Willy a price function f which takes a pair of songs [si,sj] as input, and returns a real number that quantifies exactly how good song sj sounds after song si, in her opinion. (Note that f([si,sj]) may not be equal to f([sj,si]).)
Write an O(n22n) algorithm for Willywutang that will determine a song order which maximizes the total transition goodness of the mix tape. (If the maximum is not achieved, Willy will be dumped.)
Note 1: Adapted from UC Berkeley, Spring 2001 Final Exam for CS170 (Efficient Algorithms and Intractable Problems). Approximate time you would get for this problem: 30 mins. Storyline by me :)
Note 2: This problem is pretty hard.
|
| CLOSEST POINT |
4/7/2003 12:17AM
You are given coordinates for a set of N points on a 2D plane. After preprocessing those points in some manner of your own discretion, you are given a new point v = (x,y). Now your task is to determine which of the original N points is closest in Euclidean distance to v. Devise the best algorithm (lowest big-Oh runtime) you can to accomplish this task.
Note 1: From a Mojave Networks tech-interview.
Note 2: Exactly how much time you can spend preprocessing is not specified, but I think it's reasonable to say it shouldn't be exponential. After preprocessing, the interviewer did give a runtime that your algorithm should meet for determining the point closest to v. However, I won't give that away, because it could be too much of a hint; furthermore, I am uncertain if an even better runtime does not exist.
|
| LINKED LIST DELETE |
4/10/2003 2:29PM
You are given a pointer to the middle node of a singly linked list. Delete that node.
Note: From a Mojave Networks tech-interview.
|
| ORACLE QUERIES |
5/27/2003 3:21PM
You are given n programs p1 ... pn, each of which take an ASCII string as input. Each program will either output an ACCEPT signal, or a REJECT signal, or will loop forever. You are also given n strings s1 ... sn, each affiliated with a respective program. Your task is to write a meta-program that determines which of the N program-string pairs output an ACCEPT. To assist you in this task, your meta-program is allowed to query an oracle, a black box that takes a program and a string as inputs, and immediately tells you if the computation ACCEPTs, REJECTs, or loops forever. However, you can only query the oracle log n times.
|
| QUIZ TEAM SCHEDULING |
5/27/2003 3:15PM
Consider the following problem, called Quiz Team Scheduling (QTS). You are given a set of N college students, each of which has expertise in certain academic subjects (e.g., Entomology, Cinematography, Biology, etc.). There are a total of S possible subjects. Knowing what each student is good at, you want to partition the set of students into two teams (not necessarily the same size) such that each team spans all N subjects. In other words, for any given subject, there exists at least one guy in each team which knows that subject.
So for example, the following is a YES-instance of QTS; X marks mean the student in that row knows the subject in that column:
| Entomology | Furballogy | Geology | Histology |
| Alice | X | | | X |
| Bob | | X | X | X |
| Carol | X | X | | |
| Dick | | X | X | |
Simply choose Alice and Dick for one team, and Bob and Carol for the other team.
It's easy to show that the QTS problem is in NP. By reduction from 3-SAT (yes 3-SAT specifically), show that the QTS problem is also NP-hard, and thus NP-complete.
Source: UC Berkeley CS172 (Computability and Complexity Theory) Final Exam, Spring 2003. Professor Allistair Sinclair.
|
| UNRECOGNIZABLE LANGUAGE |
5/27/2003 3:21PM
Consider the following language L:
L = { | for every input string w, M will halt within 1000|w|2 steps }
Show that this language is not recognizable. (Reduce from ~A[sub]TM[/sub].)
Note 1. denotes an encoding of a Turing machine M. So L consists of all Turing machines that satisfy the property described above.
Note 2. |w| denotes the length of the string w.
Note 3. ~A[sub]TM[/sub] = { | M is a Turing Machine that does NOT accept the string w }. So it could reject or loop forever.
Note 4. A language L is [i]recognizable[/i] if there exists a Turing Machine M such that for all strings w in L, running M on w will ACCEPT. When M is run on a string not in L, it will either REJECT or loop forever. Contrast this to a decidable language L', in which there exists a Turing Machine that will ACCEPT for strings in L', and REJECT for strings not in L'. In summary, deciders must halt, and recognizers only need to halt for strings in the language.
Source: UC Berkeley CS172 (Computablity and Complexity) Final Exam, Spring 2003
|
| C OR C++ |
5/27/2003 3:21PM
Write a program that will print "C" if compiled as an (ANSI) C program, and "C++" if compiled as a C++ program.
|
|