Author |
Topic: Series for pi (Read 879 times) |
|
Sir Col
Uberpuzzler
impudens simia et macrologus profundus fabulae
Gender: 
Posts: 1825
|
 |
Series for pi
« on: May 9th, 2007, 1:40am » |
 Quote  Modify
|
I am probably showing my ignorance here, but I was wondering if someone could shed some light on a query I have relating to the following well known infinite series for pi?
pi/4 = 1 - 1/3 + 1/5 - 1/7 + 1/9 - ...
It is usually derived using the following infinite geometric series:
S = 1 - x2 + x4 - x6 + ...
x2S = x2 - x4 + x6 - ...
S(x2+1) = 1
S = 1/(x2+1)
That is, 1/(x2+1) = 1 - x2 + x4 - x6 + ...
Integrating both sides from 0 to x gives:
arctan(x) = x - x3/3 + x5/5 - ...
And if x = 1 then we get the desired result, arctan(1) = pi/4 = 1 - 1/3 + 1/5 - 1/7 + ...
However, my query relates to the validity of allowing x to be equal to 1. Surely the infinite geometric series, from which the arctan(x) series is derived, is only valid for |x| < 1? I appreciate that this relates to the limit as x tends towards one, but it seems somewhat naļve to assume that the limit of arctan(x) and its series necessarily tend towards the desired result as x tends towards one. Is there a formal demonstration of this, or am I missing something really obvious? After all the geometric series tends towards an undefined state as x tends towards one.
|
| « Last Edit: May 9th, 2007, 1:48am by Sir Col » |
 IP Logged |
mathschallenge.net / projecteuler.net
|
|
|
Aryabhatta
Uberpuzzler
Gender:
Posts: 1321
|
|
Re: Series for pi
« Reply #1 on: May 9th, 2007, 7:54am » |
Quote Modify
|
It follows from Abel's limit theorem:
if f(x) = sum anxn (n = 1 to infinity) for |x| < r
and if sum anrn is convergent to L, then
Limit x->r- f(x) = L
|
|
IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
|
Re: Series for pi
« Reply #2 on: May 9th, 2007, 3:22pm » |
Quote Modify
|
Yes. The radius of convergence of a power series guarantees convergence in the interior, and divergence on the exterior. On the boundary the series may converge or diverge.
However, the function defined by the power series is continuous wherever the power series converges, both in the interior, and on the boundary. Since this power series is equal to arctan(x) on the interior, continuity requires they have the same value at all boundary points for which the series converges.
|
|
IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Sir Col
Uberpuzzler
impudens simia et macrologus profundus fabulae
Gender:
Posts: 1825
|
|
Re: Series for pi
« Reply #3 on: May 9th, 2007, 3:37pm » |
Quote Modify
|
That was a real "eureka" moment; I'd never properly grasped the significance of that result until now. Thanks guys.
|
|
IP Logged |
mathschallenge.net / projecteuler.net
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
|
Re: Series for pi
« Reply #4 on: May 9th, 2007, 5:04pm » |
Quote Modify
|
Of course, since it is at the very verge of divergence, you can be sure that any such series will converge slowly. Thus
 /4 = 1 - 1/3 + 1/5 - 1/7 + ...
is a very poor choice for calculating .
|
|
IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
SWF
Uberpuzzler
Posts: 879
|
|
Re: Series for pi
« Reply #5 on: May 9th, 2007, 9:11pm » |
Quote Modify
|
Although getting the right answer is tough to argue with, the ends don't justify the means. You also switched the order of integration and summation of an infinte series when it was not uniformly convergent.
You can get the series for atan(x) by expanding in a Taylor series about x=0. For a faster converging series that is not difficult to find pi, arcsin(1/2) is pretty good, but not nearly as good as some of the other methods.
|
|
IP Logged |
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
The dewdrop slides into the shining Sea
Gender:
Posts: 4489
|
|
Re: Series for pi
« Reply #6 on: May 10th, 2007, 4:34am » |
Quote Modify
|
on May 9th, 2007, 9:11pm, SWF wrote:Although getting the right answer is tough to argue with...
|
|
Can you argue with this? 
 ex = ex
ex(1 - ) = 0
ex = (1 - )-1 * 0
= ( 1 + + 2 + 3 + 4 + .......) * 0
= (1 + + + + + .......) * 0
And
0 = 1
1 = x
x = x2/2!
x2/2! = x3/3!
etc.
Hence ex = 0 + 1 + x + x2/2! + x3/3! + .......
|
| « Last Edit: May 11th, 2007, 2:35pm by ThudnBlunder » |
IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
rmsgrey
Uberpuzzler
    
Gender:
Posts: 2873
|
|
Re: Series for pi
« Reply #7 on: May 10th, 2007, 6:59am » |
Quote Modify
|
16/64
cancel the sixes...
|
|
IP Logged |
|
|
|
Aryabhatta
Uberpuzzler
Gender:
Posts: 1321
|
|
Re: Series for pi
« Reply #8 on: May 10th, 2007, 11:01am » |
Quote Modify
|
on May 9th, 2007, 9:11pm, SWF wrote:Although getting the right answer is tough to argue with, the ends don't justify the means. You also switched the order of integration and summation of an infinte series when it was not uniformly convergent.
You can get the series for atan(x) by expanding in a Taylor series about x=0. For a faster converging series that is not difficult to find pi, arcsin(1/2) is pretty good, but not nearly as good as some of the other methods.
|
|
It is not uniformly convergent in (-1,1), but isn't it the case that for any 0 < r < 1, the series is uniformly convergent in [-r,r] ?
|
|
IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
|
Re: Series for pi
« Reply #9 on: May 10th, 2007, 7:56pm » |
Quote Modify
|
on May 10th, 2007, 4:34am, ThudanBlunder wrote:
Can you argue with this?
ex = ex
(1 - )ex = 0
ex = [1/(1 - )] * 0
= ( 1 + + 2 + 3 + 4 + .......) * 0
= (1 + + + + + .......) * 0
And
0 = 1
1 = x
x = x2/2
x2 = x3/3
etc.
Hence ex = 0 + 1 + x + x2/2 + x3/3 + .......
|
|
With the corrections that you need
ex = (1 - )-1 * 0
and
x2/2 = x3/3!
etc.
and have conclusion ex = 0 + 1 + x + x2/2! + x3/3! + .......,
it can all be justified - if you define it just right.
|
| « Last Edit: May 10th, 2007, 8:34pm by Icarus » |
IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
|
Re: Series for pi
« Reply #10 on: May 10th, 2007, 11:07pm » |
Quote Modify
|
on May 10th, 2007, 4:34am, ThudanBlunder wrote:
Can you argue with this? |
|
It would make more sense to do the following: Define a linear operator T by
(Tf)(x) = 0x f(t)dt,
and let
Un = I + T + T2 + ... + Tn.
If 1 is the function given by 1(x) = 1 for all x, then
(I - T)Un1 = (I - Tn+1)1 = 1 - xn+1/(n+1)!,
which converges to 1, say in L1(0,1), or C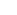 (0,1), or uniformly on compacta, or some such. In other words, letting A be the operator I-T, and fn = Un1, then
Afn  1 = A(ex),
and we want to conclude fn ex. That is, is A-1 continuous?
Note that, in L1 norm,  Tf < f for all f 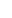 0, so A is one-to-one. But in fact Tn = 1 for all n, so Un does not converge in operator norm, although Un1 does converge. For which f does Unf converge?
|
| « Last Edit: May 10th, 2007, 11:14pm by Eigenray » |
IP Logged |
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
The dewdrop slides into the shining Sea
Gender:
Posts: 4489
|
|
Re: Series for pi
« Reply #11 on: May 11th, 2007, 2:04pm » |
Quote Modify
|
on May 10th, 2007, 7:56pm, Icarus wrote:
With the corrections that you need
ex = (1 - )-1 * 0
and
x2/2 = x3/3!
etc.
and have conclusion ex = 0 + 1 + x + x2/2! + x3/3! + .......,
it can all be justified - if you define it just right.
|
|
Yes, how careless of me! Now corrected. (I was a little drunk at the time.) 
Also, I remember from when I studied elementary differential equations that differential operators can also be manipulated as though they are linear operators.
|
| « Last Edit: May 11th, 2007, 2:39pm by ThudnBlunder » |
IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
The dewdrop slides into the shining Sea
Gender:
Posts: 4489
|
|
Re: Series for pi
« Reply #12 on: May 11th, 2007, 3:34pm » |
Quote Modify
|
on May 10th, 2007, 11:07pm, Eigenray wrote:
It would make more sense to do the following: Define a linear operator T by
(Tf)(x) = 0x f(t)dt,
and let
Un = I + T + T2 + ... + Tn.
If 1 is the function given by 1(x) = 1 for all x, then
(I - T)Un1 = (I - Tn+1)1 = 1 - xn+1/(n+1)!,
which converges to 1, say in L1(0,1), or C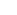(0,1), or uniformly on compacta, or some such. In other words, letting A be the operator I-T, and fn = Un1, then
Afn 1 = A(ex),
and we want to conclude fn ex. That is, is A-1 continuous?
Note that, in L1 norm, Tf < f for all f 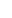0, so A is one-to-one. But in fact Tn = 1 for all n, so Un does not converge in operator norm, although Un1 does converge. For which f does Unf converge? |
|
Are these Banach spaces?
|
|
IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
|
Re: Series for pi
« Reply #13 on: May 11th, 2007, 6:18pm » |
Quote Modify
|
on May 11th, 2007, 2:04pm, ThudanBlunder wrote:| Also, I remember from when I studied elementary differential equations that differential operators can also be manipulated as though they are linear operators. |
|
They are linear operators. Unfortunately they tend to be unbounded, and not everywhere defined.
on May 11th, 2007, 3:34pm, ThudanBlunder wrote:
L1(0,1) and C(0,1) are Banach, but the normed space C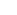(0,1) isn't (a uniform limit of smooth functions need not be smooth). And the topology of compact convergence doesn't even come from a norm.
|
|
IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
|
Re: Series for pi
« Reply #14 on: May 11th, 2007, 6:53pm » |
Quote Modify
|
You can make C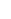 a Banach space too, but you have to use a Sobolev norm.
And while the topology of compact convergence doesn't come from a norm, it still makes C0 a complete topological vector space - so the essentials of a Banach space are still there.
|
| « Last Edit: May 11th, 2007, 6:56pm by Icarus » |
IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print