Author |
Topic: Differential Equations on a Torus (Read 6751 times) |
|
Deedlit
Senior Riddler
Posts: 476
|
 |
Re: Differential Equations on a Torus
« Reply #25 on: May 14th, 2005, 12:00am » |
 Quote  Modify
|
on May 13th, 2005, 7:56pm, Michael_Dagg wrote:
I bet your instructor was disappointed.
The solution is a space curve in R3 and with some work you can produce it. |
|
Hmmm... it looks to me like a family of surfaces. At each point, the tangent space is restricted to a plane.
|
|
 IP Logged |
|
|
|
Deedlit
Senior Riddler
Posts: 476
|
|
Re: Differential Equations on a Torus
« Reply #26 on: May 14th, 2005, 12:13am » |
Quote Modify
|
on May 13th, 2005, 7:19am, Michael_Dagg wrote:
One of the more interesting that comes to mind is a Lie group. |
|
Lie groups are by far the most well-known and studied of such groups, so I bet that's what he had in mind.
For everyone else, a Lie group is a group with the structure of an analytic manifold, such that the group operations are analytic. (that is, xy and x-1 are analytic - but we can just assume the first, and the second comes for free.) The most common examples are linear transformations of vector spaces, like GLn(C), Spn(R), etc. The study if Lie groups is surprisingly deep and connected. A related neat category are the Lie algebras - the tangent spaces to a Lie group at the identity.
Another interesting "hybrid" class of groups are the topological groups - groups with a topological structure, such that the group operations are continuous.
|
|
IP Logged |
|
|
|
Michael Dagg
Senior Riddler
Gender: 
Posts: 500
|
|
Re: Differential Equations on a Torus
« Reply #27 on: May 14th, 2005, 8:51am » |
Quote Modify
|
on May 14th, 2005, 12:00am, Deedlit wrote:
Hmmm... it looks to me like a family of surfaces. At each point, the tangent space is restricted to a plane.
|
|
p(x,y,z) = (x^2 + y^2)/(z(x + y)) = c
or
x^2 + y^2 - c(x + y)z = 0
or
z = (c^-1)(x^2 + y^2)/(x + y)
|
|
IP Logged |
Regards,
Michael Dagg
|
|
|
skydiver
Guest
|
|
Re: Differential Equations on a Torus
« Reply #28 on: May 14th, 2005, 11:42am » |
Quote Modify
 Remove
|
on May 14th, 2005, 8:51am, Michael_Dagg wrote:
p(x,y,z) = (x^2 + y^2)/(z(x + y)) = c
|
|
That solution works! I would be very appreciative to get the details on how you solved it. I see that you can look at it as either a family of surfaces or just a single curve since every curve that makes the surface is also a solution.
|
|
IP Logged |
|
|
|
Michael Dagg
Senior Riddler
Gender:
Posts: 500
|
|
Re: Differential Equations on a Torus
« Reply #29 on: May 15th, 2005, 2:06pm » |
Quote Modify
|
You will appreciate a method of solution much more if you derive it yourself. It is not that difficult. You are looking for a solution of the form p(x,y,z) =c.
Hint: Try to eliminate one of the differentials to reduce it to the form M(u,v)du + N(u,v)dv = 0 and then integrate it.
What book did you use for this class?
|
|
IP Logged |
Regards,
Michael Dagg
|
|
|
skydiver
Guest
|
|
Re: Differential Equations on a Torus
« Reply #30 on: May 16th, 2005, 8:26am » |
Quote Modify
Remove
|
The book we used is Diff Equations by Nagle, Saff, Snyder. The problem did not come from the book. It was on the final.
I tried endlessly to reduce it to an equation that contained only two diffs. Most of the time I would get an equation more complex than it and if I remember I did manage to eliminate z a fews ways but could never eliminate dz.
|
|
IP Logged |
|
|
|
Ken Wiley
Guest
|
|
Re: Differential Equations on a Torus
« Reply #31 on: May 16th, 2005, 4:15pm » |
Quote Modify
Remove
|
Humm... I tried a few things and too and the equation just got bigger instead of getting reduced. I suppose the magic is in the right substituion. If the two polys on the dx and dy terms were factorable then perhaps one or more factors could be divided out but they aren't over the real numbers. I am not sure that I can see how to get z to vanish since it is a multiplier for the dx and dy terms.
|
|
IP Logged |
|
|
|
StonedAgain
Guest
|
|
Re: Differential Equations on a Torus
« Reply #32 on: May 16th, 2005, 5:18pm » |
Quote Modify
Remove
|
on May 16th, 2005, 4:15pm, Ken Wiley wrote:| I suppose the magic is in the right substituion. |
|
I agree and it is like they pop up with a substitution out of nowhere and it works.
|
|
IP Logged |
|
|
|
Michael Dagg
Senior Riddler
Gender:
Posts: 500
|
|
Re: Differential Equations on a Torus
« Reply #33 on: May 16th, 2005, 11:01pm » |
Quote Modify
|
You form substitutions based on what you are given, which of course are expressions upon which they are to be applied.
As for magic substitutions, they are only magic for those who know not.
The N,S,S diferential equations text is fairly widely used and is a good one to study from. The latter two authors publish a complex analysis text that is in my opinon a very good book if you want to learn complex analysis right after the calculus sequence. It was actually wrote for that purpose but it does not require hardly any linear algebra or differential equations.
Regarding the differential equations problem at present, you can eliminate both z and dz from the TDE if you substitute x = uz and y = vz. You will arrive at a TDE that is of the form I mentioned, Mdx + Ndy = 0, such that you can integrate for the solution in terms of u and v, but note that since you introduced the substitution you must convert it back to the original several variables equation in x,y,z.
|
| « Last Edit: May 17th, 2005, 8:29am by Michael Dagg » |
IP Logged |
Regards,
Michael Dagg
|
|
|
skydiver
Guest
|
|
Re: Differential Equations on a Torus
« Reply #34 on: May 19th, 2005, 8:12am » |
Quote Modify
Remove
|
Still doesn't reduce with x = uz and y = vz. What am doing wrong?
|
|
IP Logged |
|
|
|
Michael Dagg
Senior Riddler
Gender:
Posts: 500
|
|
Re: Differential Equations on a Torus
« Reply #35 on: May 20th, 2005, 3:05pm » |
Quote Modify
|
on May 19th, 2005, 8:12am, skydiver wrote:| Still doesn't reduce with x = uz and y = vz. What am doing wrong? |
|
There is no way for us to know what you are doing wrong since you did not write anything.
Check your algebra and confirm you differentiated the substitutions correctly. That is, given x = uz and y = vz, then dx = udz + zdu and dy = vdz + zdv.
|
|
IP Logged |
Regards,
Michael Dagg
|
|
|
Michael Dagg
Senior Riddler
Gender:
Posts: 500
|
|
Re: Differential Equations on a Torus
« Reply #36 on: Jun 17th, 2005, 6:54pm » |
Quote Modify
|
Skydiver I take it that you have given up on this differential equation?
|
|
IP Logged |
Regards,
Michael Dagg
|
|
|
Skydiver
Guest
|
|
Re: Differential Equations on a Torus
« Reply #37 on: Jul 3rd, 2005, 8:44am » |
Quote Modify
Remove
|
I did manage to finally eliminate z and dz and came up with a DE in terms of u and v that was easy to integrate. It wasn't all that easy though - a lot of algebra was needed for the elimination.
|
|
IP Logged |
|
|
|
Michael Dagg
Senior Riddler
Gender:
Posts: 500
|
|
Re: Differential Equations on a Torus
« Reply #38 on: Jul 7th, 2005, 8:47pm » |
Quote Modify
|
What does the reduction look like?
|
|
IP Logged |
Regards,
Michael Dagg
|
|
|
Skydiver
Guest
|
|
Re: Differential Equations on a Torus
« Reply #39 on: Jul 9th, 2005, 9:13am » |
Quote Modify
Remove
|
Here is it abbreviated
M(u,v) dx + N(u,v) dy = 0
with
M(u,v) = a/b
N(u,v) = g/b
a = u2 + 2uv - v2
b = (u2 + v2)(u + v)
g = v2 + 2uv - u2
Integrating gives
log((u2 + v2)/(u + v))
(u2 + v2)/(u + v) = C
and when you substitute u = x/z and v = y/z you get
(x2 + y2)/(xz + yz) = C
|
|
IP Logged |
|
|
|
Michael Dagg
Senior Riddler
Gender:
Posts: 500
|
|
Re: Differential Equations on a Torus
« Reply #40 on: Jul 10th, 2005, 8:40am » |
Quote Modify
|
Nice work.
|
|
IP Logged |
Regards,
Michael Dagg
|
|
|
uMROD
Guest
|
|
Re: Differential Equations on a Torus
« Reply #41 on: Jul 10th, 2005, 4:01pm » |
Quote Modify
Remove
|
That is an interesting derivation of solution. I was not surprised to see those u,v polynoms in the integrals since there were x,y polynoms in parts of the DE.
Is is possible to pluck out the potential and kinetic energy component of the pendulum:
ma2 Q" + mga sin(Q) = 0, where m=mass, g=gravity, and a = length of swing, and Q is the angle of swing.
|
|
IP Logged |
|
|
|
Ken Wiley
Guest
|
|
Re: Differential Equations on a Torus
« Reply #42 on: Jul 11th, 2005, 9:23am » |
Quote Modify
Remove
|
on Jul 10th, 2005, 4:01pm, uMROD wrote:| Is is possible to pluck out the potential and kinetic energy component of the pendulum: |
|
I am not completely sure, but I think they have to be given numerically since the pendulum solution cannot be given in terms of elementary functions. This is one of the things I vividly remember about the pendulum. I recall from physics that if you can get one of the energies then most of the time you can compute the other.
|
|
IP Logged |
|
|
|
Michael Dagg
Senior Riddler
Gender:
Posts: 500
|
|
Re: Differential Equations on a Torus
« Reply #43 on: Jul 11th, 2005, 11:00am » |
Quote Modify
|
You can deduce expressions for both energies.
Since Q" = Q' (dQ'/dQ),
ma^2 Q" + mga sin(Q) = ma^2 Q' dQ'/dQ + mga sin(Q) = 0.
Integrating with respect to Q we get
ma^2 int[Q' dQ'] + mga int[sin(Q) dQ] = c
and therefore
1/2 ma^2 Q'^2 - mga cos(Q) = c.
The last equation expresses the conservation of energy of the pendulum. The first term is the kinetic energy and the second term is the potential energy. By choosing different values of c we can study any possible motion and compute one energy or the other. As you can see, the sum of the kinetic energy and the potential energy is constant.
Also note that the reduced form (first order equation) is, so to speak, explicitly more nonlinear that the second order form and it too cannot be expressed in terms of elementary functions. The phase portrait of the system plotted in the (Q,Q') plane reveals the behavior of the system and from studying it you can deduce a linear approximation to any given trajectory.
|
|
IP Logged |
Regards,
Michael Dagg
|
|
|
Ken Wiley
Guest
|
|
Re: Differential Equations on a Torus
« Reply #44 on: Jul 12th, 2005, 6:38am » |
Quote Modify
Remove
|
That reduction had me stumped since I sat for quite sometime looking at Q" = Q' (dQ'/dQ) before I decided to try to come up with it, more tricks with differential relationships.
It is interesting that the kinetic energy graph is a parabola but not surprising.
|
|
IP Logged |
|
|
|
Skydiver
Guest
|
|
Re: Differential Equations on a Torus
« Reply #45 on: Jul 12th, 2005, 5:41pm » |
Quote Modify
Remove
|
I plugged the right side of Q" into Matlab but it did not give me Q" back until I specifed a variable to which Q is differentiated with respect to. When it did, it displayed dQ2/dt2 which is the same thing.
|
|
IP Logged |
|
|
|
ConeHead
Guest
|
|
Re: Differential Equations on a Torus
« Reply #46 on: Jul 12th, 2005, 9:03pm » |
Quote Modify
Remove
|
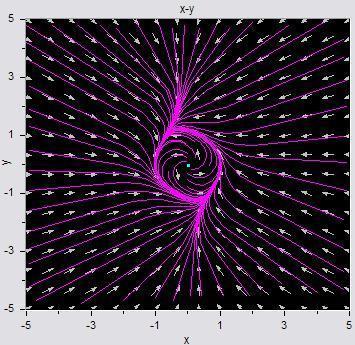
Show that the system has a periodic solution:
x' = x - y - (x2 + 3/2 y2)x
y' = x + y - (x2 + 1/2 y2)y
|
|
IP Logged |
|
|
|
SWF
Uberpuzzler
Posts: 879
|
|
Re: Differential Equations on a Torus
« Reply #47 on: Jul 12th, 2005, 10:32pm » |
Quote Modify
|
on Jul 11th, 2005, 11:00am, Michael_Dagg wrote:
Since Q" = Q' (dQ'/dQ),
...
Integrating with respect to Q we get |
|
You can also multiply the equation by Q' and integrate on time to get the same thing.
Same thing can be done to Newton's 2nd law:
F = m * d2y/d t2
Multiply by dy/dt and integrate to get change in kinetic energy equals work done.
|
|
IP Logged |
|
|
|
Michael Dagg
Senior Riddler
Gender:
Posts: 500
|
|
Re: Differential Equations on a Torus
« Reply #48 on: Jul 15th, 2005, 8:13am » |
Quote Modify
|
on Jul 12th, 2005, 9:03pm, ConeHead wrote:Show that the system has a periodic solution:
|
|
This problem falls in the intermediate level of study. It can be shown that the given system has a periodic solution by various means. But more importantly would be a solution that most everyone would understand and could likely spark a trail of nice discussions.
The first step would be to plot the phase portrait of the system, say, within the bounds (-5,5) x (-5,5) and post the graphic.
|
| « Last Edit: Jul 15th, 2005, 9:03am by Michael Dagg » |
IP Logged |
Regards,
Michael Dagg
|
|
|
Ken_Wiley
Newbie
Gender:
Posts: 22
|
Let me kick it off, here's the plot
Re:
x' = x - y - (x2 + 3/2 y2)x
y' = x + y - (x2 + 1/2 y2)y
|
| « Last Edit: Jul 15th, 2005, 7:18pm by Ken_Wiley » |
IP Logged |
 |
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print