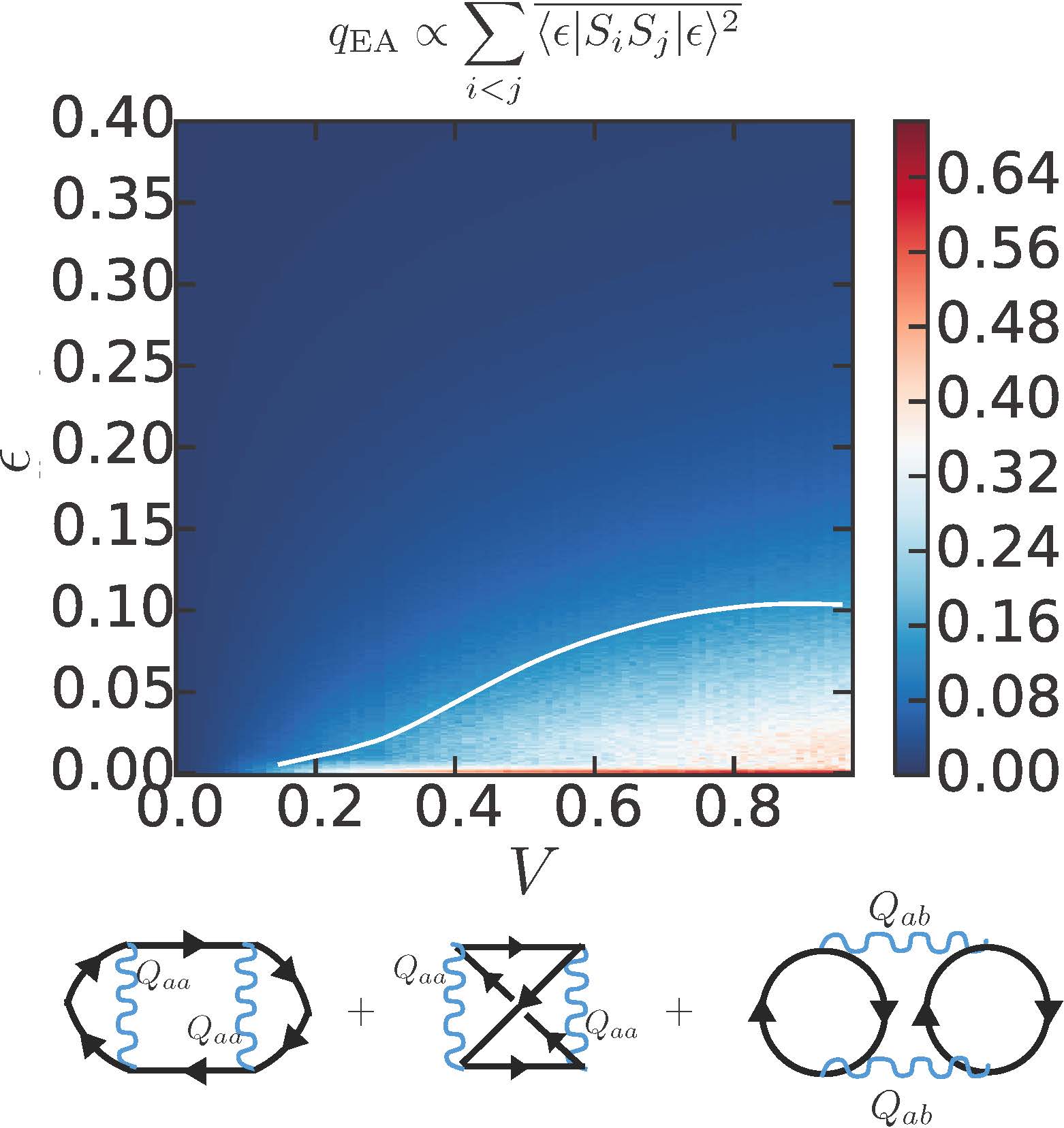Ergodic quantum systems generically exhibit chaotic dynamics and ‘‘scramble’’ quantum information. Recently, very general arguments have been put forth suggesting that there even exist universal bounds on how fast these processes may occur: in particular, it has been proposed that the Lyapunov exponent \(\lambda_L\), which sets a time scale for the growth of chaos, has an upper bound \(\lambda_L \leq 2\pi k_{B}T/\hbar\) at low temperatures \(T\).

The Sachdev-Ye-Kitaev (SYK) model is an analytically solvable model of strongly interacting fermions that saturates this bound on chaos. We extend it by adding random two-site (density-density) interactions of the form \(\sum_{ij} V_{ij} n_i n_j\)—this term is a standard example of a glass, namely the Sherrington-Kirkpatrick model. If sufficiently strong, this term can, in principle, lead to a dynamical quantum phase transition from the ergodic (chaotic) SYK state to a glassy, non-ergodic state.

We investigate this transition both numerically, using exact diagonalization, and analytically, using an expansion in fluctuations around the SYK fixed point. We study the instability toward replica symmetry-breaking (a hallmark signature of glassiness) induced by the two-site interactions and we find that a transition occurs at a temperature \(T_{g} \propto \exp\left(-\alpha J/V\right)\), where \(J/V\) is the relative strength of the ergodic term with respect to the charge glass term.

Figure: Phase diagram in the plane of the strength \(V\) of the charge glass interactions (in units of \(J=1\)) and the energy density \(\epsilon\). The color map corresponds to the value of the glass—Edwards-Anderson—order parameter \(q_{\mathrm{EA}}\). (below) The relevant Feynman diagrams at second order \(\mathcal{O}(V^2)\) in perturbation theory: only the third one contributes to the Edwards-Anderson order parameter.

Work in preparation.

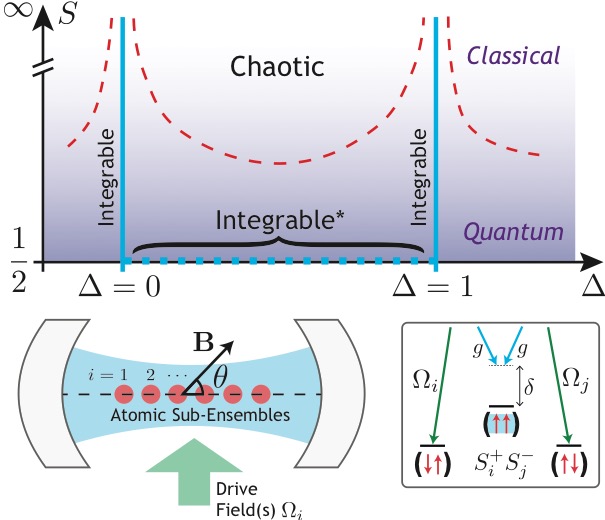In this project, we study a class of spin models with random all-to-all interactions that is akin to the SYK model described above. However, the difference between the two is responsible for an even richer dynamical phase diagram, which includes regions of chaos, integrability, and of a novel form of integrability that we term ‘‘integrable\(^{*}\).’’

First, we show that there exist two special values for a model parameter \(\Delta\) where the system is integrable for any value of the spin size \(S\), as well as in the classical limit: at \(\Delta=0\) and \(\Delta=1\) the model is equivalent to various versions of the Gaudin-Richardson model and it possesses an extensive family of 2-body conserved quantities.

Second, we identify a novel integrable structure at \(0<\Delta<1\) that, crucially, depends on the spin size \(S\): we present numerical evidence that the quantum dynamics is integrable for \(S=1/2\), whereas the classical dynamics is chaotic. We also find that the conserved charges are no longer purely 2-body, but that they develop ‘‘dressing tails'' on higher-body terms, reminiscent of the local integrals of motion in MBL.

Last, we propose an experimental implementation in a system of atomic ensembles trapped in a single-mode optical cavity that would enable the systematic exploration of these various dynamical phases of matter.

This platform therefore represents a new paradigm for studying integrability, chaos, and thermalization under closed many-body quantum dynamics.

Figure: Phase diagram in the plane of the anisotropy \(\Delta\) along the \(z\)-axis and the spin size \(S\). The model has three integrable lines: at \(\Delta=0,1\) for any value of \(S\); and a novel integrable line at intermediate \(0<\Delta<1\) for \(S=1/2\). The classical system (\(S\rightarrow \infty\)) exhibits chaotic dynamics with a non-zero Lyapunov exponent. The conjectured phase boundary between chaos and integrability is schematically depicted by the red dashed lines. (below) The experimental setup in which the model can be implemented.

Reference: G. Bentsen\(^{\dagger}\), IDP\(^{\dagger}\), V. Bulchandani, T. Scaffidi, X. Cao, X.-L. Qi, M. Schleier-Smith, E. Altman, ‘‘Integrable and Chaotic Dynamics of Spins Coupled to an Optical Cavity,’’ Phys. Rev. X 9, 041011.

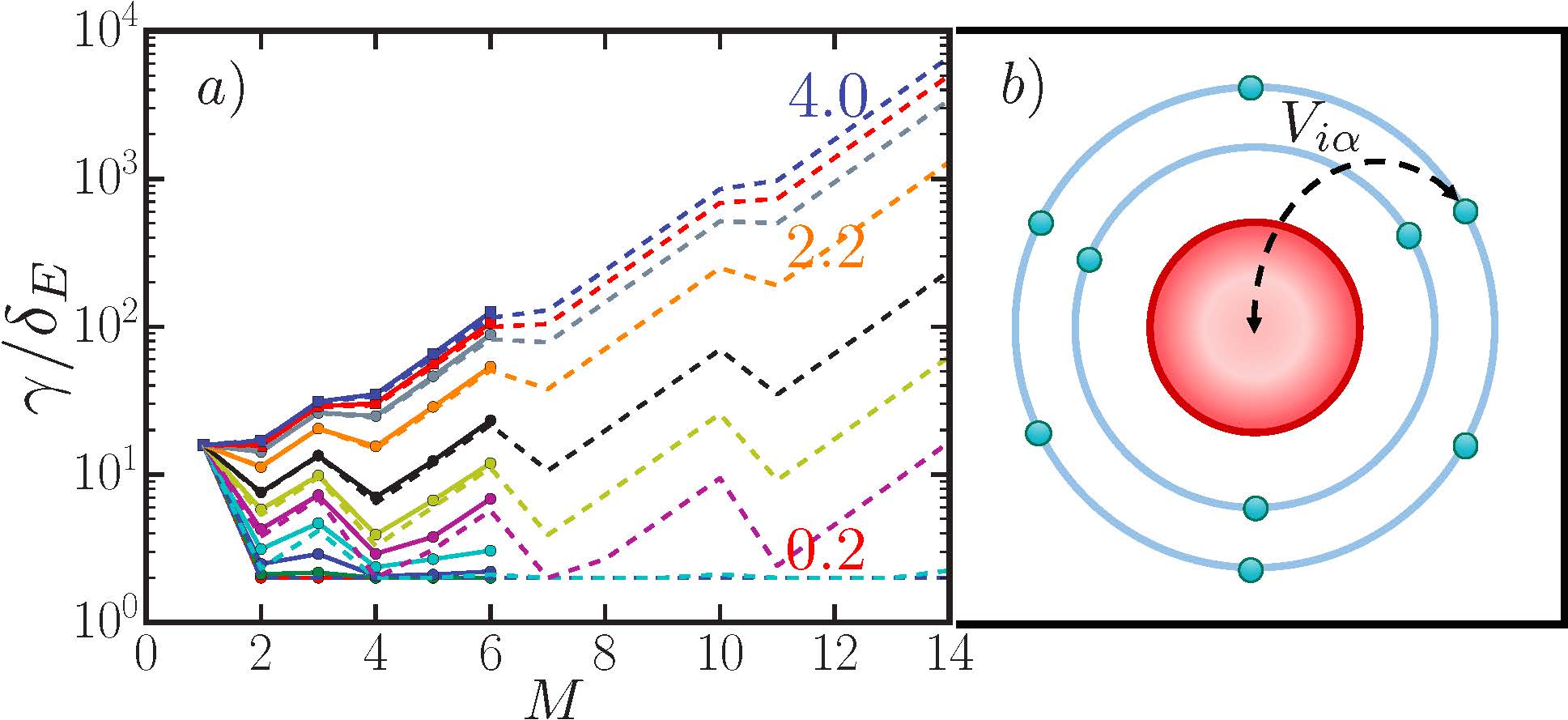Thus far, we have studied two types of non-ergodic dynamics: glassy and integrable, respectively. A third example is the so-called Many-Body Localized (MBL) state, which is a generalization of ...the phenomenon of Anderson localization—P.W. Anderson showed that, depending on the spatial dimension \(d\), an electron hopping on a lattice in the presence of a random potential can become trapped (or localized) at a given site. MBL is an extension of this idea to the more generic and complicated case of many, interacting, and quantum particles.

Similar to single-particle localization, the spatial dimension \(d\) appears to be crucial for MBL. Work by De Roeck et al. [Phys. Rev. B 95, 155129 (2017)] has argued that MBL is unstable in two and higher dimensions due to a thermalization avalanche triggered by rare regions of weak disorder. According to this narrative, such regions, naturally occurring in a 2D material, will thermalize the degrees of freedom in their vicinity, which, in turn, will increase the overall size of the region and lead to the avalanche.

To examine these arguments, we construct several models of a finite ergodic bubble coupled to an electronic insulator. We first describe the ergodic region using a random matrix and perform an exact diagonalization study of small systems. We find excellent agreement with a refined theory of the thermalization avalanche.

We then explore the limit of large system sizes by modeling the ergodic region via a Hubbard model with all-to-all random hopping which gives us an analytic handle. We find that the ergodic region may change dramatically when it is weakly coupled to a large number of degrees of freedom in its vicinity. This emergent effect cannot be predicted by the avalanche paradigm. Moreover, it may even lead to the failure of the avalanche for a given size of the ergodic bubble. Nonetheless, the effect is suppressed and the avalanche can be recovered if the ergodic region is larger.

Figure: (left) The width \(\gamma\) of the spectral function peaks as a function of the number \(M\) of additionally coupled degrees of freedom for different values of the localization length \(\xi\) (different colors). The solid curves are obtained numerically, whereas the dashed curves are obtained analytically using the refined avalanche theory. (right) The \(d=2\) geometry we consider.

Reference: IDP, S. Banerjee, E. Altman, ‘‘Exploration of the stability of many-body localization in \(d>1\),’’ Phys. Rev. B 99, 205149.

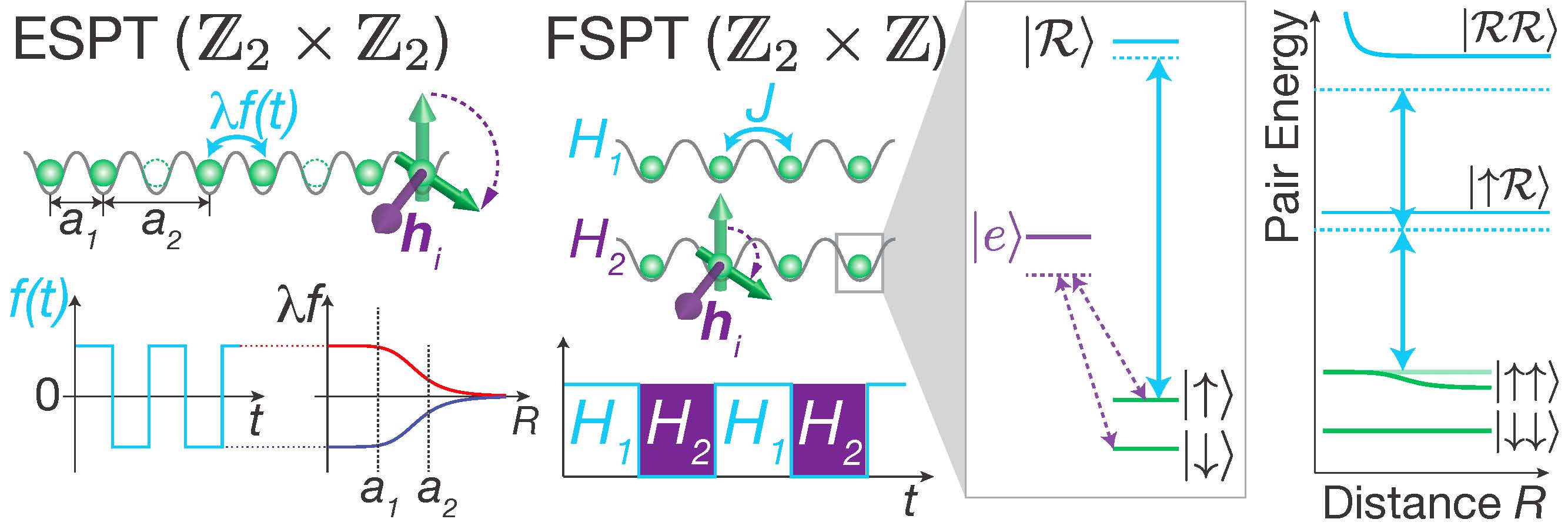Symmetry-protected topological (SPT) order lies outside the conventional Ginzburg-Landau paradigm of classifying phases of matter based on symmetry-breaking. A hallmark ...signature of SPT phases is the existence of edge (boundary) modes that are robust to local perturbations that do not break the symmetry (thus the name). A famous example is the topological insulator. Moreover, the fact that these SPT systems have robust edge modes, capable of coherently storing quantum information indefinitely provided that the symmetry is never broken, makes them a very interesting candidate for quantum computation.

While SPT order has been historically studied as a zero-temperature, \(T=0\), property (namely a property of the ground state), Many-Body Localization enables its generalization to all states of a disordered system.

In this project, we propose and analyze two distinct routes toward realizing interacting SPT phases via periodic driving. First, we demonstrate that a driven transverse-field Ising model can be used to engineer complex interactions which enable the emulation of an equilibrium (undriven) SPT phase. This phase remains stable only within a parametric time scale controlled by the driving frequency, beyond which its topological features break down.

To overcome this issue, we consider an alternate route based upon realizing an intrinsically Floquet SPT phase that does not have any equilibrium analog. In both cases, we show that disorder, leading to MBL, prevents runaway heating and enables the observation of coherent quantum dynamics at high energy densities.

Finally, we propose a unifying implementation in a one-dimensional chain of Rydberg-dressed atoms and show that protected edge modes are observable on realistic experimental time scales.

Figure: Experimental proposal for engineering the two types of SPTs that we analyze: on the left, the emulation of an SPT protected by \(\mathbb{Z}_2\times \mathbb{Z}_2\); on the right, an intrinsically-driven SPT protected by \(\mathbb{Z}_2 \times \mathbb{Z}\) (\(\mathbb{Z}\) corresponds to the discrete time translation symmetry).

Reference: IDP, A. C. Potter, M. Schleier-Smith, A. Vishwanath, N. Y. Yao, ‘‘Floquet symmetry-protected topological phases in cold atomic systems,’’ Phys. Rev. Lett. 119, 123601.

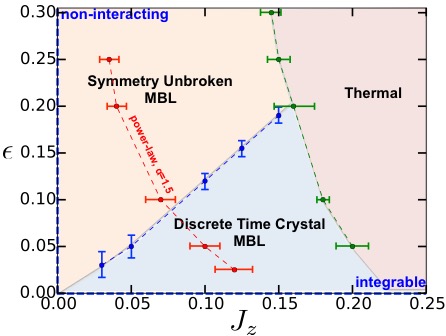As mentioned before, many phases of matter can be understood within the conceptual framework of symmetry-breaking. For instance, a Bose-Einstein Condensate is an exotic \(U(1)\) symmetry-broken phase, whereas a crystal such as ice breaks the translational symmetry observed in liquid water.

A very interesting and natural question is whether it is possible to break time translation symmetry? By analogy with the ‘‘freezing’’ transition of a liquid (spatial symmetry-unbroken) into a crystal (spatial symmetry-broken), this would lead to a phase that can be called a ‘‘time crystal.’’

It has been previously shown that the spontaneous breaking of continuous time translation (\(t \rightarrow t+ \delta t\), where \(\delta t \in \mathbb{R}\)) cannot occur in isolated, interacting, many-body systems at thermal equilibrium. Remarkably, however, it is possible to break the discrete time translation symmetry that occurs in a periodically-driven (Floquet) system. Such a driven, interacting, and many-body quantum system is symmetric under discrete time translations \(t \rightarrow t + T\), where \(T\) is the period of the driving field. In a time crystal, the symmetry is broken down to a smaller subgroup of translations \(t \rightarrow t + nT\), where \(n \in \mathbb{Z}\) and \(n\geq 2\). Notably, this \(nT\) period of the time crystal is caused by a combination of collective synchronization—stabilized by the many-body interactions—and Many-Body Localization, which prevents runaway heating. Moreover, this phase of matter is dual to the Floquet-SPT phase, protected by \(\mathbb{Z}_2\times\mathbb{Z}\), which was discussed in the previous section.

In one project[1], we consider a simple model for realizing a time crystal in a system with one spatial dimension. We present evidence of the crystalline rigidity as the drive field is varied and we describe the dynamical transition wherein the time crystal ‘‘melts'' into a trivial Floquet insulator.

Secondly, we propose an experimental blueprint for realizing this phase and transition in a one dimensional chain of trapped ions. This proposal has been implemented in two different physical systems, including on the trapped ions platform, and the time crystal has been observed for the first time[2].

Figure: Phase diagram in the plane of the interaction strength \(J_z\) and the pulse imperfection \(\epsilon\). The model has three phases: the time crystal (symmetry-broken) phase, the trivial paramagnetic (symmetry-unbroken) phase, and the thermal phase (since the amount of disorder is limited due to the nature of the drive).

[1] Theory: N. Y. Yao, A. C. Potter, IDP, A. Vishwanath, ‘‘Discrete time crystals: rigidity, criticality, and realizations,’’ Phys. Rev. Lett. 118, 030401
[2] Experiment: J. Zhang, P. W. Hess, A. Kyprianidis, P. Becker, A. Lee, J. Smith, G. Pagano, IDP, A. C. Potter, A. Vishwanath, N. Y. Yao, C. Monroe, ‘‘Observation of a Discrete Time Crystal,’’ Nature volume 543, p.217

See also: Physics Viewpoint and Nature News & Views.

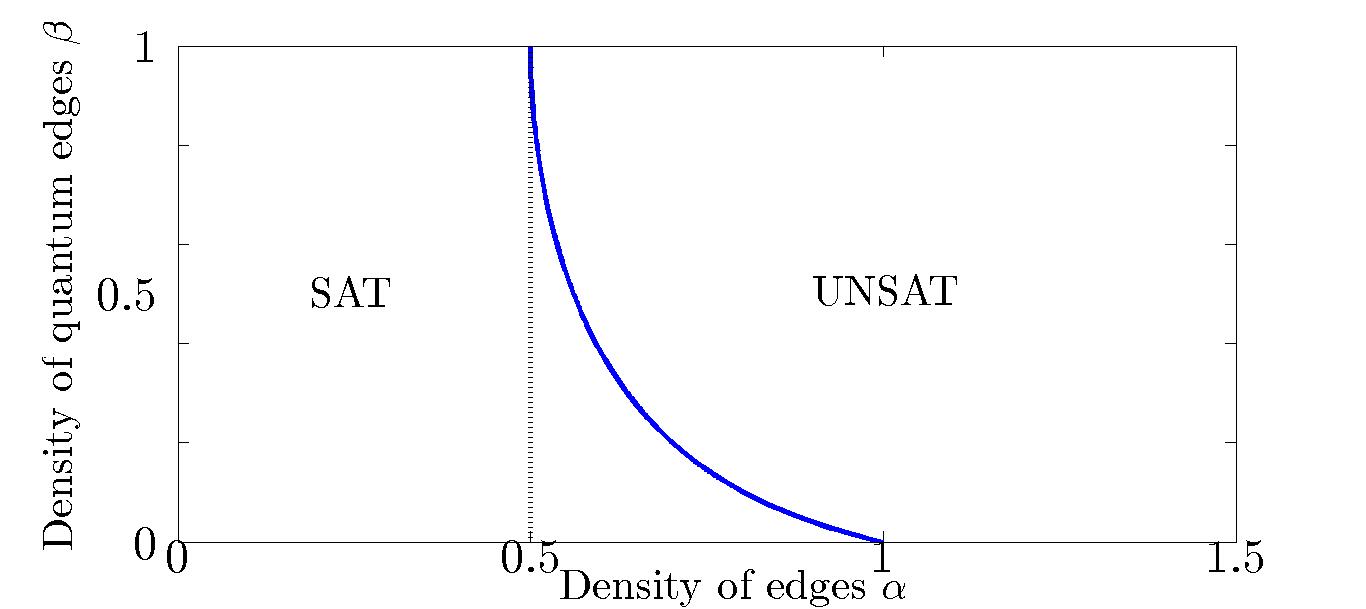The random interactions present in a spin glass create frustration, which, in turn, leads to a very rugged energy landscape of accessible states. The basic intuition behind ‘‘glassy'' dynamics is that, as the system explores ...the phase space, it gets successively trapped in local minima (meta-stable states) and it takes a very long time to find the global minimum. This is reminiscent of the narrative in many optimization problems in the theory of computation—an algorithm can get successively stuck on many sub-optimal solutions for a long time before it finds the optimal one. In fact, Y.-T. Fu and P.W. Anderson have conjectured that there is a deep connection between NP-complete (colloquially ‘‘hard'' optimization) problems and the physics of glasses.

Classical satisfiability (\(k\)-SAT) and quantum satisfiability (\(k\)-QSAT) for \(k>2\) are complete problems for the complexity classes NP and QMA, which are believed to be intractable for classical and quantum computers, respectively. Statistical ensembles of instances of these problems have been studied previously in an attempt to elucidate their typical, as opposed to worst case, behavior.

In this project, we introduce a new statistical ensemble that interpolates between the classical and quantum regimes. For the simplest 2-SAT/2-QSAT ensemble (\(k=2\) SAT and QSAT are in P and BQP, respectively) we find the exact boundary that separates SAT and UNSAT instances. We do so by establishing coincident lower and upper bounds, in the limit of large instances, on the extent of the UNSAT and SAT regions, respectively.

Figure: Phase diagram in the plane of the density of edges \(\alpha = M/N\) (\(M\) is the number of edges in a graph of \(N\) vertices) and the density \(\beta\) of quantum edges (\(1-\beta\) edges are classical). The dashed line at \(\alpha=1/2\) indicates the emergence of a giant component in the random graph (the percolation phase transition). \(\beta = 0\) corresponds to the 2-\(\mathrm{SAT}\) problem and \(\beta = 1\) corresponds to the 2-\(\mathrm{QSAT}\) problem.

Reference: IDP, C. R. Laumann, S. L. Sondhi, ‘‘Classical-Quantum Mixing in the Random 2-Satisfiability Problem,’’ Phys. Rev. A 92, 040301 (Rapid Communication).

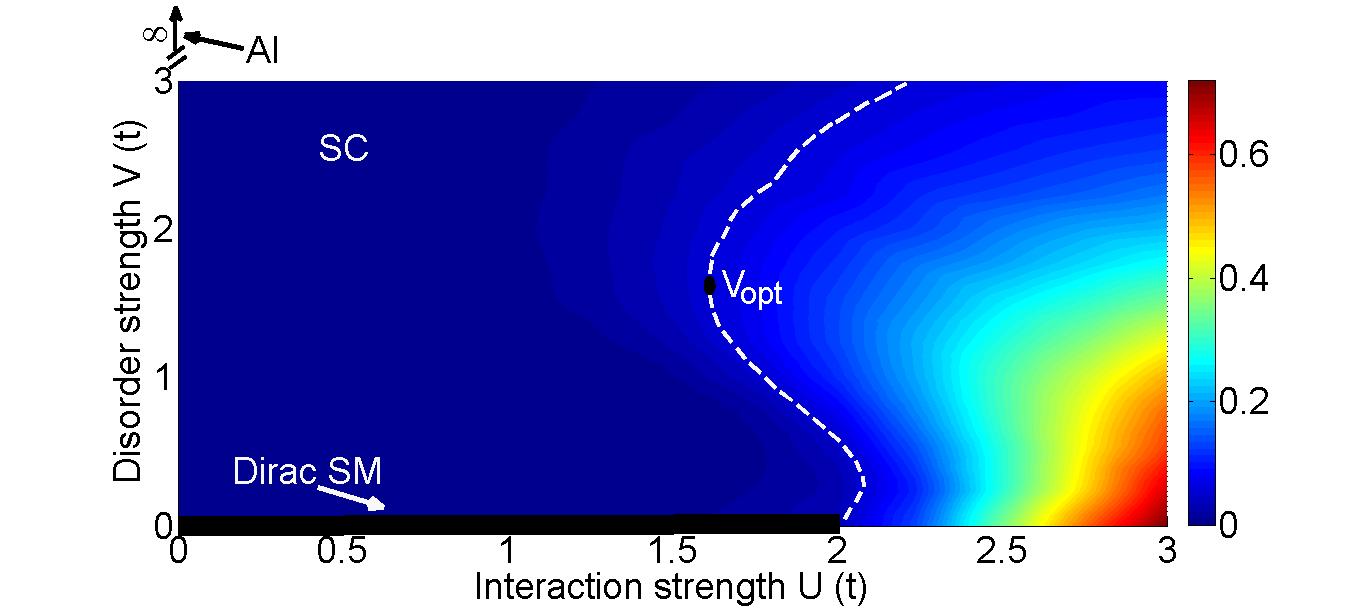We study the interplay between superconductivity and disorder in a sheet of graphene with on-site attractive interactions using a spatially inhomogeneous self-consistent ... approach. In the absence of disorder there are two phases at charge neutrality. Below a critical value \(U_c\) for the attractive interactions there is a Dirac semimetal phase and above it there is a superconducting phase.

The numerical solution of the self-consistency equations suggests that, while in the strong attraction regime (\(U > U_c\)) disorder has the usual effect of suppressing superconductivity, in the weak attraction regime (\(U < U_c\)) weak disorder enhances superconductivity. In the weak attraction regime, disorder that is too strong eventually suppresses superconductivity, i.e. there is an optimal disorder strength that maximizes the critical temperature \(T_c\). Our numerical results also suggest that in the weakly disordered regime, mesoscopic inhomogeneities enhance superconductivity significantly more than what is predicted by a spatially uniform mean-field theory à la Abrikosov-Gorkov. In this regime, superconductivity consists of rare phase-coherent superconducting islands. This rare regions effect—along with the one encountered in the stability of MBL in \(d>1\)—is an example of Griffiths physics.

Lastly, we study the enhancement of the superconducting proximity effect by disorder and mesoscopic inhomogeneities, and obtain results that can be directly compared to scanning tunneling miscroscopy (STM) experiments on proximity-induced superconductivity in graphene.

Figure: The phase diagram in the plane of the interaction strength \(U\) and the disorder strength \(V\). We plot the order parameter (local pairing amplitude) \(\Delta_{\mathrm{op}}\) as a heat map. SC is the superconductor; Dirac SM is the Dirac semimetal; AI is the Anderson insulator; and \(V_{\mathrm{opt}}\) is the optimal disorder. Below the critical coupling (\(U < U_c\)), weak disorder enhances superconductivity, while strong disorder suppresses it. For stronger interactions \(U > U_c\), disorder suppresses superconductivity.

Reference: IDP, J. Maciejko, R. Nandkishore, S. L. Sondhi, ‘‘Superconductivity of disordered Dirac fermions in graphene,’’ Phys. Rev. B 90, 094516.