Tobin Fricke, April 2004.
The Hoshen-Kopelman Algorithm is a simple algorithm for labeling clusters on a grid, where a grid is a regular network of cells, where each cell may be either "occupied" or "unoccupied". The HK algorithm is an efficient means of identifying clusters of contiguous cells.
The algorithm was originally described in "Percolation and cluster distribution. I. Cluster multiple labeling technique and critical concentration algorithm," by J. Hoshen and R. Kopelman and printed in Phys. Rev. B. 1(14):3438-3445 in October 1976. The article is available in PDF from Physical Review Online Archive (subscription required). However, the HK-algorithm is really just a special application of the Union-Find algorithm, well known to computer scientists. The use of the union/find abstraction also makes description of the H-K algorithm far more transparent than without.
The general idea of the H-K algorithm is that we scan through the grid looking for occupied cells. To each occupied cell we wish to assign a label corresponding to the cluster to which the cell belongs. If the cell has zero occupied neighbors, then we assign to it a cluster label we have not yet used (it's a new cluster). If the cell has one occupied neighbor, then we assign to the current cell the same label as the occupied neighbor (they're part of the same cluster). If the cell has more than one occupied neighboring cell, then we choose the lowest-numbered cluster label of the occupied neighbors to use as the label for the current cell. Furthermore, if these neighboring cells have differing labels, we must make a note that these different labels correspond to the same cluster.
The Union-Find algorithm is a simple method for computing equivalence classes. Calling the function union(x,y) specifies that items x and y are members of the same equivalence class. Because equivalence relations are transitive, all items equivalent to x are equivalent to all items equivalent to y. Thus for any item x, there is a set of items which are all equivalent to x; this set is the equivalence class of which x is a member. A second function find(x) returns a representative member of the equivalence class to which x belongs.
It is easy to describe the H-K algorithm in terms of union and find operations, and coding the algorithm with reference to union and find subroutines is more likely to result in a correct program than a more haphazard implementation technique.
The HK algorithm consists of a raster scan of the grid in question. Each time an occupied cell is encountered, a check is done to see whether this cell has any neighboring cells who have already been scanned. If so, first a union operation is performed, to specify that these neighboring cells are in fact members of the same equivalence class. Then a find operation is performed to find a representative member of that equivalence class with which to label the current cell. If, on the other hand, the current cell has no neighbors, it is assigned a new, previously unused, label. The entire grid is processed in this way. The grid can then be raster-scanned a second time, performing only `find' operations at each cell, to re-label the cells with their final assignment of a representative element. This is easy to describe in pseudocode:
largest_label = 0;
for x in 0 to n_columns {
for y in 0 to n_rows {
if occupied[x,y] then
left = occupied[x-1,y];
above = occupied[x,y-1];
if (left == 0) and (above == 0) then /* Neither a label above nor to the left. */
largest_label = largest_label + 1; /* Make a new, as-yet-unused cluster label. */
label[x,y] = largest_label;
else if (left != 0) and (above == 0) then /* One neighbor, to the left. */
label[x,y] = find(left);
else if (left == 0) and (above != 0) then /* One neighbor, above. */
label[x,y] = find(above);
else /* Neighbors BOTH to the left and above. */
union(left,above); /* Link the left and above clusters. */
label[x,y] = find(left);
}
}
}
One application is in the modeling of percolation or electrical conduction. If occupied cells are made of copper and unoccupied cells of glass, then a cluster is a group of electrically connected cells. Cells touch in the four cardinal directions, but not diagonally. Here's an example:
|
In this matrix, 1's represent occupied cells; 0's are unoccupied cells. |
This is the result of applying the Hoshen-Kopelman algorithm to the grid on the left. Contiguous clusters are labeled. |
to do: re-render the above diagrams using CSS; automatically adjust the cell dimensions to be uniform and square
This is a description of an implementation of the Union-Find algorithm. We begin by assuming that there are a maximum of N equivalence classes. Note that this is the maximum number of intermediate equivalence classes, which may be greater than the final number of equivalence classes — an extreme upper bound for the number of equivalence classes is the number of items (grid cells in the case of the HK algorithm) which are being sorted into equivalence classes. (I suppose this is a form of the pigeonhole principle: If you have X things in Y classes, then Y is less than X.)
We maintain an array of N integers, called "labels," whose elements have the following meaning: if labels[a]==b then we know that labels a and b correspond to the same cluster; initially we set labels[x]=x for all x (initially, each element is in its own equivalence class; initially each element is not equivalent to any other). Furthermore we impose the requirement that a >= b. In this way, we can set up chains of equivalent labels. Simple versions of the find and union functions are immediately apparent:
int labels[N]; // initialized to labels[n]=n for all n
int find(int x) { // naive (but correct) implementation of find
while (labels[x] != x)
x = labels[x];
return x;
}
The union function makes two labels equivalent by linking their respective chains of aliases:
void union(int x, int y) {
labels[find(x)] = find(y);
}
Note that the result x = find(x) will have the property label[x] == x, which is the defining property for x to be the representative member of its equivalence class. The correctness of the union function can be gleaned from this fact.
[The original HK algorithm used the convention that negative label[x] values indicated that x was an alias of another label, while a positive value indicated that label[x] was the canonical label. This positive value was incremented every time an element was added to the equivalence class — the result was that the labels array would give not only the structure of the equivalence classes, but the total number of elements in each one as well. It's a good idea, and the implementation given here could easily be modified to do that. However, it's probably simpler to just loop over the final labelled matrix and count the number of sites in each class.]
An improvement is to allow find to collapse the tree of aliases:
int find(int x) {
int y = x;
while (labels[y] != y)
y = labels[y];
while (labels[x] != x) {
int z = labels[x];
labels[x] = y;
x = z;
}
return y;
}
to do: add a diagram showing how the label aliases form a set of trees
Given an implementation of the union-find algorithm in the functions uf_find, uf_union, and uf_makeset, the Hoshen-Kopelman algorithm becomes very simple:
for (int i=0; i<m; i++)
for (int j=0; j<n; j++)
if (matrix[i][j]) { // if occupied ...
int up = (i==0 ? 0 : matrix[i-1][j]); // look up
int left = (j==0 ? 0 : matrix[i][j-1]); // look left
switch (!!up + !!left) {
case 0:
matrix[i][j] = uf_make_set(); // a new cluster
break;
case 1: // part of an existing cluster
matrix[i][j] = max(up,left); // whichever is nonzero is labelled
break;
case 2: // this site binds two clusters
matrix[i][j] = uf_union(up, left);
break;
}
}
It should be obvious how to generalise this for higher dimensions.
A complete implementation in the C language is given here in the file hk.c.
In MATLAB, the image processing toolbox comes with a function bwlabel that does cluster labelling.
I don't have any FORTRAN implementation (as has often been requested). If someone would like to contribute one, I would include the code here.
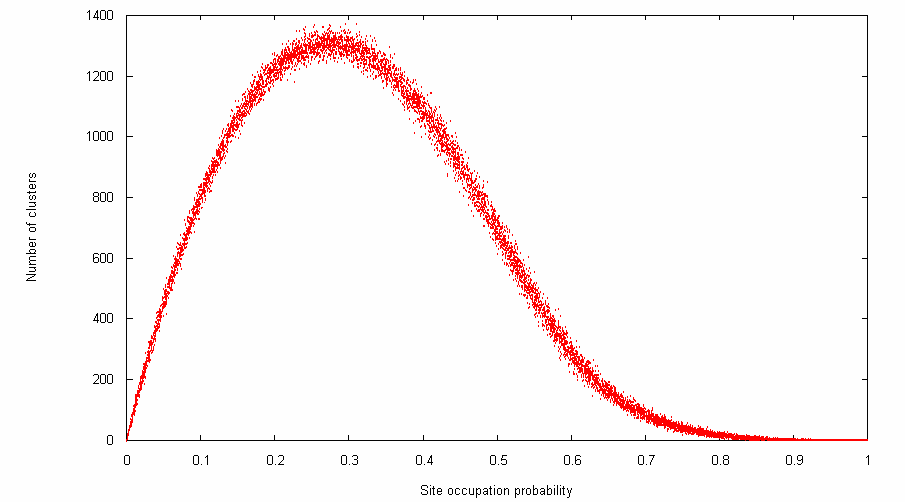
One might be interested in the relationship between site occupation probability and the resulting number of clusters. The following program generates random matricies each with a randomly chosen site occupation probability, and outputs on each line the site occupation probability that was used and the number of clusters in the resulting matrix.
int main(int argc, char **argv) {
int m = 100;
int n = 100;
int n_trials = 10000;
// allocate our matrix
int **matrix = (int **)calloc(m, sizeof(int*));
for (int i=0; i<m; i++)
matrix[i] = (int *)calloc(n, sizeof(int));
for (int trial = 0; trial < n_trials; trial ++) {
float p = rand()/(float)RAND_MAX;
// make a random matrix with site occupancy probability p
for (int i=0; i<m; i++)
for (int j=0; j<n; j++)
matrix[i][j] = (rand() < p*RAND_MAX);
// count the clusters
int clusters = hoshen_kopelman(matrix,m,n);
printf("%f %d\n",p,clusters);
}
return 0;
}
Here's a visualisation of the output, made using gnuplot:

It might also be interesting to plot the size of the largest cluster versus site occupation probability, or the distribution of cluster sizes for a given probability, etc. Another project would be to adapt the HK algorithm to work on a non-square grid (such as a hexagonal grid).
Copyright © 2000 by Tobin Fricke. Last modified 21 April 2004.