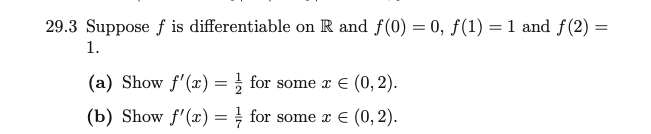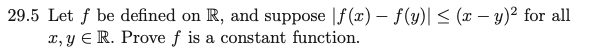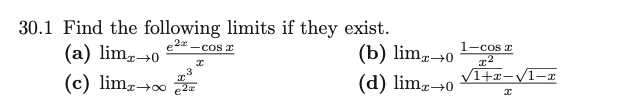Due Monday (Nov 29) 9pm. problem 6 contains a typo, and it is updated now.

1. In class we have seen that a function $f(x)$ may be differentiable everywhere, but the derivative function $f'(x)$ is not continuous. In this problem, we will see that discontinuity is not a removable singularity. Assume $f: \R \to \R$ is differentiable. Assume that $\lim_{x \to 0} f'(x) = 1$. Prove that $f'(0)=1$. (Hint, you can use mean value theorem, and definition of the $f'(0)$. )

2. If $f: [0,1] \to \R$ is a differentiable function such that $f'(0)=f'(1)=0$, is it true that there exists a $c \in (0,1)$, such that $f'( c) = 0$ as well? If not, give a counter-example.

3. Ross Ex 29.3

4. Ross Ex 29.5

5. Ross Ex 30.1

6. Prove that $\lim_{x \to 0^+} x^{-n} e^{-1/x} = 0$. Hint: let $u = 1/x$, and turn the problem into a $u \to \infty$ limit calculation, then Taylor expand $e^u = 1 + u + u^2/2! + \cdots + u^n / n! + \cdots$. (There was a typo in the first version, I wrote $x^{n} e^{-1/x}$ instead. You can either do the wrong problem, or do the corrected ones. )

1. Assume that $\lim_{x \to 0} f'(x) = 1$. Prove that $f'(0)=1$. (Hint, you can use mean value theorem, and definition of the $f'(0)$. )

By mean value theorem for interval $[0,\delta]$, we have $\frac{f(\delta)-f(0)}{\delta - 0} = f'(x_\delta)$ for some $x_\delta \in (0, \delta)$. Thus as $\delta \to 0$, $x_\delta \to 0$, hence $\lim_{\delta \to 0}\frac{f(\delta)-f(0)}{\delta - 0} = \lim_{\delta \to 0} f'(x_\delta) = \lim_{x \to 0} f'(x)1$

2. If $f: [0,1] \to \R$ is a differentiable function such that $f'(0)=f'(1)=0$, is it true that there exists a $c \in (0,1)$, such that $f'( c) = 0$ as well? If not, give a counter-example.

It may not be true. Let $g(x)= e^{-1/x}$ for $x \in (0,1]$ and $g(0)=0$. Then $g'(0)=0$. Let $f(x) = g(x) / (g(x) + g(1-x))$. We can prove that $f(x)$ is strictly monotone in $(0,1)$, and $f(0)=0, f(1)=1$.

3. Ross Ex 29.3

Consider the interval $[0,2]$, the slope of the segment $\frac{f(2)-f(0)}{2-0} = 1/2$, hence there is an $x_1 \in (0,2)$, such that $f'(x_1)=1/2$.

Consider the interval $[1,2]$, by mean value theorem, there is a $x_2 \in (1,2)$, such that $f'(x_2)=0$.

By the intermediate value theorem, since $1/7 \in (0,1/2)$, there is an $x_3 \in (x_1, x_2)$ or $(x_2,x_1)$, such that $f'(x_3) = 1/7$.

4. Ross Ex 29.5

We can prove that $f'(x)=0$ for all $x$, indeed, we have $\lim_{h\to 0} \left| \frac{ f(x+h) - f(x)}{h} \right| \leq \lim_{h\to 0} h = 0.$ Thus, for any $x_1, x_2 \in \R$, we may apply the mean value theorem to get $f(x_1) - f(x_2) = (x_1 - x_2) f'(x_3) = 0$ for some $x_3 \in (x_1, x_2)$.

5. Ross Ex 30.1

(a) Taking derivatives once both upstairs and downstairs, we get $\lim_{x\to 0} \frac{2 e^{2x}+\sin(x)}{1} = 2$

(b) Taking derivatives twice both upstairs and downstairs, we get $\lim_{x\to 0} \frac{\cos(x)}{2} = 1/2$

(c ) Taking derivatives 3 times both upstairs and downstairs, we get $\lim_{x \to \infty} \frac{6}{8 e^{2x}} = 0$

(d) Taking derivative once, we get $\lim_{x \to 0} \frac{1/2}{\sqrt{1+x}} + \frac{1/2}{\sqrt{1-x}} = 1/2+ 1/2=1$

6. Prove that $\lim_{x \to 0^+} x^{-n} e^{-1/x} = 0$.

Let $u = 1/x$, then we are computing $\lim_{u\to \infty} u^n / e^{u}$ We may apply L'Hopital rule n times, and get $\lim_{u\to \infty} u^n / e^{u} = \lim_{u\to \infty} n! e^{-u} = 0.$