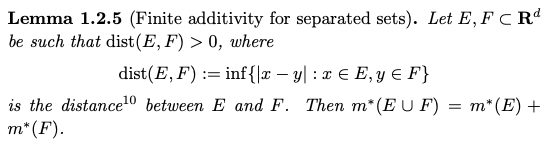HW2
Due on gradescope next Friday 6pm. Please also submit on discord sometime around Wednesday.
So far, we have climbed the 'one face' of the mountain Lebesgue measure, let's climb the other face. 1) Here are some guides. Our goal is to start from the alternative definition of measurability (see Lecture 4, bottom),
Def 2 : A subset $E$ is measurable, if for any $\epsilon>0$, there exists an open set $U\supset E$, such that $m^*(U \RM E) < \epsilon$.
and derive the same set of properties for measurable sets. Note that, all the properties of outer-measure can still be used.
In the following, the measurability is defined using Def 2 above.
Lemma 0
(stolen from Tao's grad measure theory book)
Lemma 1
Let $A$ be any subset of $\R^n$, then $$ m^*(A) = \inf \{ m^*(U) \mid U \supset A, U \text{ is open } \} $$
Lemma 2
If $\{E_i\}$ is a countable collection of measurable set, then $\cup_i E_i$ is measurable.
Lemma 3
Every closed subset $A \In \R^n$ is measurable.
Hint: This is a hard one. First prove that $A$ can be written as countable union of bounded closed subsets, then suffice to prove the claim that any bounded closed (hence compact) subset $A$ is measurable.
Hint 2: Given $A$ a closed bounded subset of $\R^n$, for any $\epsilon>0$, we have some open set $U$ with $m^*(U) < m^*(A) + \epsilon$. Then we just need to show that $m^*(U \RM A) < \epsilon$. Note $U\RM A $ is open. Claim: for any closed subset $K \in U \RM A$, we have $m^*(K) + m^*(A) = m^*(A \cup K) \leq m^*(U)$, hence $m^*(K) < \epsilon$. The key point is to show that there exists an increasing sequence of closed subsets $K_n \In U \RM A$, such that $\lim m^*(K_n) = m^*(U \RM A)$. Try to construct $K_n$ as finite union of almost disjoint closed boxes, e.g., use the dyadic subdivision trick.
What does a closed set look like? Say, the cantor set in $[0,1]$?
Lemma 4
If $E$ is measurable, then $E^c$ is measurable.
Hint: Try to write $E^c$ as a countable union of closed sets, union a set of measure zero, hence is countable.
