Table of Contents
$$\gdef\d\partial$$
2020-02-05 Metric Tensor
Recall that if $V$ is a vector space, then a metric tensor of $V$ is an element $g \in V^* \otimes V^*$, that is symmetric and positive definite, i.e.
- (symmetric) for any $v, w \in V$, $g(v,w) = g(w, v)$.
- (positive definite), for any $v \in V$ and $v \neq 0$, $g(v,v) > 0$.
If we have a basis $\{e_i\}$ for $V$, and corresponding dual basis $\{h^i\}$ for $V^*$, then the metric tensor can be written as $$ g = \sum_{i,j=1}^n g_{ij} h^i \otimes h^j, \quad g_{ij} = g(e_i, e_j). $$ Note: if someone give you a vector space (over $\R$), then by default, it does not come equipped with a metric tensor. The data of a metric tensor is upto your choice.
Recall that for any point $p \in \R^n$, $T_p \R^n$ is the tangent space at $p$. We define a metric tensor at point $p$ to be a metric tensor $g_p$ for the vector space $T_p \R^n$.
Note: that, for two distinct points $p, q \in \R^n$, $T_p \R^n$ and $T_q \R^n$ do not “talk to each other”, and $g_p$ and $g_q$ has nothing to do with each other.
If we have a basis $\{ e_i(p) \}_{i=1}^n$ for the tangent space $T_p \R^n$, then we can write the metric tensor in components. We denote $$ g_{ij}(p) = g_p(e_i(p), e_j(p)). $$ One can think of $g_{ij}(p)$ as an $n$ by $n$ matrix, whose entries depends on $p$.
Example 1: Flat space $\R^3$ in Cartesian coordinate
This is the space that we live in, hence the most important one in some sense.
Let $(x, y, z)$ be the Cartesian coordinate system on $\R^3$. For a point $p \in \R$, we can have a basis $\d_x|_p, \d_y|_p, \d_z|_p$ of $T_p \R^3$. The metric tensor $g_p$ of $T_p \R^3$ is defined by the following rules $$ g_p(\d_x|_p, \d_x|_p) = 1, \quad g_p(\d_y|_p, \d_y|_p) = 1, \quad g_p(\d_z|_p, \d_z|_p) = 1 $$ and all other components are zero, i.e. $$ g_p( \d_x|_p, \d_y|_p) = g_p(\d_x|_p, \d_z|_p) = g_p(\d_y|_p, \d_z|_p) = 0. $$
If we call $e_1(p) = \d_x|_p, e_2(p) = \d_y|_p, e_3(p) = \d_z|_p$, then we have $g_{ij}(p) = \delta_{ij}$. This is a special case that, the components $g_{ij}(p)$ does not depends on $p$.
Notation : I will sometimes omit the dependence of $p$, and write $\d_x$ instead of $\d_x|_p$, $e_i$ instead of $e_i(p)$.
What can a metric tensor do? It can measure the length of a tangent vector. For example, suppose $v = (1,0,2) \in T_p \R^3$, and $w = (2,1,1) \in T_p \R^3$, then we can compute $$ g_p(v, w) = g_p( e_1 + 2 e_3, 2 e_1 + e_2 + e_3) = g_p(e_1, 2 e_1) + g_p(2 e_3, e_3) = 2 + 2 = 4 $$ of course, you can say this gives the same answer as $$ (1,0,2) \cdot (2,1,1) = 1 \cdot 2 + 0 \cdot 1 + 2 \cdot 1 = 2 + 2 = 4. $$
So far, all familar stuff, maybe a bit boring. Let's look at some other examples.
Example 2: Flat space $\R^3$ in Cylindrical coordinate
We use cylindrical coordinate $(r, \theta, z)$. We will first write down the coordinate transformation matrix with the Cartesian coordinate $(x,y,z')$ (To avoid using the $z$ variable twice, we denote this second $z$ as $z'$, just for clarity of notation.)
The transformation rule is $$ r = \sqrt{x^2+y^2}, \quad \theta = \arctan(y/x),\quad z = z' $$ and the transformation rule in the other direction is $$ x = r \cos\theta, \quad y = r \sin \theta, \quad z' = z. $$
Then for a point $p \in \R^3$, we can write down the change of basis rule for $T_p \R^3$, between $\{ \d_r, \d_\theta, \d_z$ and $\d_x, \d_y, d_{z'}$. $$ \d_r = \frac{\d x} {\d r} \d_x + \frac{\d y} {\d r} \d_y + \frac{\d z'} {\d r} \d_{z'} = \cos\theta \d_x + \sin \theta \d_y $$ $$ \d_\theta = \frac{\d x} {\d \theta} \d_x + \frac{\d y} {\d \theta} \d_y + \frac{\d z'} {\d \theta} \d_{z'} = -r\sin\theta \d_x + r \cos \theta \d_y $$ $$ \d_z = \frac{\d x} {\d z} \d_x + \frac{\d y} {\d z} \d_y + \frac{\d z'} {\d z} \d_{z'} = \d_{z'} $$ I wrote all the intermediate step there, just to show that, the formula is quite straightforward, and you just need to take the partial derivatives to get the coefficients in the expansions.
Now, we can write down the various components of the metric tensor $g$ in the new basis $$ g(\d_r, \d_r) = g(\cos\theta \d_x + \sin \theta \d_y, \cos\theta \d_x + \sin \theta \d_y ) = (\cos \theta)^2 + (\sin \theta)^2 = 1 $$ $$ g(\d_r, \d_\theta) = g(\cos\theta \d_x + \sin \theta \d_y, -r\sin\theta \d_x + r \cos \theta \d_y) = \cos\theta \cdot (-r\sin\theta) + \sin \theta \cdot (r \cos \theta) = 0 $$ The computation used bilinearity of $g$ (linear in each slot), and the components of $g$ in $\d_x, \d_y, \d_z$.
And I summarize the rest: $$ g(\d_\theta, \d_\theta) = r^2, \quad g(\d_z, \d_z) = 1, \quad g(\d_r, \d_z) = 0, \quad g(\d_z, \d_\theta)=0. $$
Example 3: flat $\R^3$ in spherical coordinates
Exercise, repeat what we do for the cylindrical coordinate.
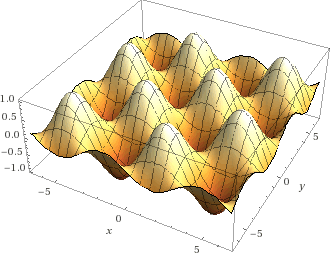
Example 4: A wavy surface
Let $f(x, y) = \sin(x)\sin(y)$, and let $\Gamma_f$ be its graph, that is
$$\Gamma_f = \{(x,y,z) \in \R^3 \mid z = f(x,y) \}. $$
Here is a picture, plotted using Wolfram alpha
Parametrization of $\Gamma_f$ , we will parametrize points on $\Gamma_f$ using its $(x,y)$ coordinates, to be clear, we call them $(u,v)$. That is $$ \phi : \Gamma_f \to \R^2_{u,v}, \quad u(x,y,z)=x, \; v=(x,y,z) = y. $$ And since $\phi$ is 1-to-1, we can have the inverse $$ \phi^{-1}: \R^2_{u,v} \to \Gamma_f, \quad x(u,v) = u, \; y(u,v) = v, \; z(u,v) = \sin(u) \sin(v). $$
We will define a metric on $\R^2_{u,v}$. For a point $p \in \R^2_{u,v}$, and tangent vectors $\d_u$ and $\d_v$, they corresponds to point $P = \phi^{-1}(p) \in \Gamma_f$, and tangent vectors $\phi^{-1}_*(\d_u)$ and $\phi^{-1}_*(\d_v)$ in $T_P \Gamma_f$. The notations are horrible, but hopefully the formulas are not so bad: $$ \phi^{-1}_*(\d_u) = \frac{\d x}{\d u} \d_x + \frac{\d y}{\d u} \d_y + \frac{\d z}{\d u} \d_z = \d_x + \cos(u) \sin(v) \d_z $$ $$ \phi^{-1}_*(\d_v) = \frac{\d x}{\d v} \d_x + \frac{\d y}{\d v} \d_y + \frac{\d z}{\d v} \d_z = \d_y + \sin(u) \cos(v) \d_z $$ Then, we are in business. We can compute the metric tensor $g_p$ on $T_p \R^2$, using the metric tensor $g_P$ of $T_P \Gamma_f$, which is the same as $g_P$ of $T_P \R^3$, since $\Gamma_f$ sits inside $\R^3$.
$$g_p (\d_u, \d_u) = g_P( \phi^{-1}_*(\d_u), \phi^{-1}_*(\d_u)) = g(\d_x + \cos(u) \sin(v) \d_z , \d_x + \cos(u) \sin(v) \d_z ) = 1 + \cos(u)^2 \sin(v)^2 $$ similarly $$g_p (\d_v, \d_v) = 1 + \sin(u)^2 \cos(v)^2 $$ and the “mix term” $$ g_p(\d_u, \d_v) = g(\d_x + \cos(u) \sin(v) \d_z, \d_y + \sin(u) \cos(v) \d_z) = \cos(u)\sin(u)\cos(v)\sin(v). $$

