This week we studied curvature and connections, in particular the Levi-Cevita connection on the tangent bundle. It is important to do some calculation to see that our intuition agrees with the formula and calculationd. Many nice things happens for Lie groups

1. Let $M$ be the unit shpere $S^2$, and let $(\theta, \phi)$ be spherical coordinates on it. For $\theta_0 \in (0, \pi)$, let $\gamma=\gamma^{(\theta_0)}$ be the circle with $\theta = \theta_0$ $\gamma: [0, 1] \to S^2, \quad t \mapsto (\theta_0, 2 \pi t)$ Let $u_0 = \d_\phi \in T_{\gamma(0)}S^2$ be a tangent vector to the curve. What is the resulting tangent vector after parallel transport $u_0$ one round along long $\gamma$?

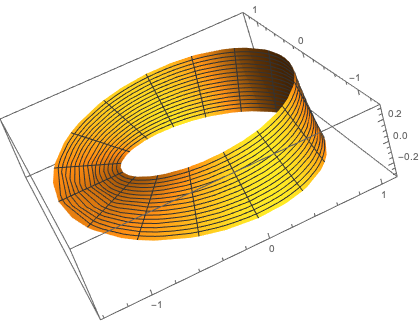
2. Let $M$ be a Mobius band of unit radius and width $2\delta$ in $\R^3$, that is, $M$ is the image of the map $(0, 2\pi] \times (-\delta, \delta) \to \R^3$ where $(\phi, z) \mapsto ((1 + z \sin (\phi/2) ) \cos \phi, (1 + z \sin (\phi/2) ) \sin \phi, z \cos(\phi/2) )$ Question: is the induced metric on $M$ flat?

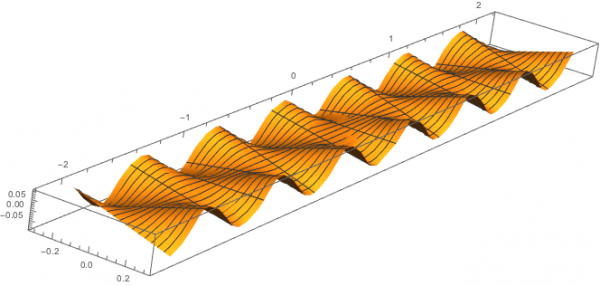
3. (Wiggly band): Let $M$ be a submanifold of $\R^3$ defined by the following embedding $\R \times (-\delta, \delta) \to \R^3$ $(t, z) \mapsto ( z \cos ( \sin t ) , z \sin (\sin t) ), t)$ Prove that the metric is not flat. For example, compute the curvature associated to the Levi-Cevita connection, and show that it is not identically zero.

4. Exercise 4.1.20 in [Ni]. Let $G$ be a Lie group. $X, Y \in T_e G$. Show that the parallel transport of $X$ along $exp(t Y)$ is given by $L_{\exp( (t/2) Y )*} R_{\exp( (t/2) Y )*} X.$

5. Compute the Killing form for $su(2)$ and $sl(2, \R)$.