1. (Geodesics are length extremizing). Recall the following facts

• Consider the space $\R^2$. If we equip $\R^2$ with the flat metric, then it is well-known that every of two points has a unique geodesic connecting them.
• Consider the sphere $S^2$, if we equip $S^2$ with the usual round metric, then every pair of two points (not antipodal pairs) has exactly two geodesics connecting them.

Here comes the question: we will equip $\R^2$ with a metric as following $$ g = \iota^* (g_{\R^3}), \quad \iota: \R^2 \to \R^3, \quad (x,y) \mapsto (x,y, h_r(x,y))$$ where $$h_r(x,y) = r^{-2} e^{ - (x^2+y^2)/r^2}$$ is a Guassian peak with radius $r$ and height $r^{-2}$. Answer the following question without doing computation:

1. Let $p = (-1,0)$, $q = (1,0)$. As $r \to \infty$, how many geodesics are there between $p$ and $q$?
2. As $r \to 0$, how does the amount of geodesics between $p$ and $q$ changes?
3. Is it possible that for any finite $r$, there are only finitely many geodesics between $p$ and $q$?

Here is a picture, and the Mathematica program to make that picture (FYI, you can use Mathematica for free as Berkeley student!) In the program, I fixed the initial point, and varies shooting angle, and the peak height.

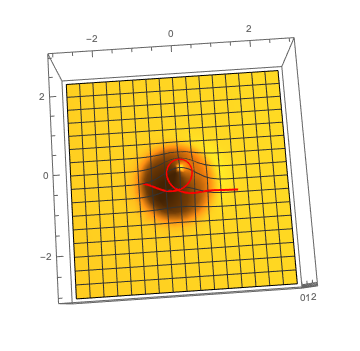
And here is a video:

2. Let $S$ be the submanifold of $\R^3$, that arises as the graph of $x^2 - y^2$. Compute the second fundamental form of $S$ at $x=0, y=0$.

3. Let $G$ be a compact Lie group with a bi-invariant metric $\la -,- \ra$. Let $X, Y, Z$ be left-invariant vector fields. (try to do it yourself before checking Example 4.2.11 in [Ni]). Show that $$ R(X, Y) Z = (-1/4) [ [X, Y], Z] $$

4. (Cartan 3-form). Same setup as 3. There is $3$-form $B$ on $G$, satisfying $$B(X, Y, Z) = \la [X, Y], Z \ra. $$ Show that this form is closed. In the case $G = SU(2) \cong S^3$, can you recognize this $3$-form as something familiar?

Hint: use the invariant formula for exterior derivative, and plug in the left-invariant vector fields.

5. (Normal Coordinate.) Ex 4.1.43. Hint: choose nice coordinate and nice basis.