 Author
Author |
Topic: 0.999... (Read 35941 times) |
|
Michael Dagg
Senior Riddler
   

Gender: 
Posts: 500
|
 |
Re: 0.999...
« Reply #100 on: Dec 15th, 2006, 5:18pm » |
 Quote Quote  Modify Modify
|
on Dec 15th, 2006, 8:35am, A-man wrote:| Last two posts seem to contradict each other. |
|
No they don't (why?).
|
|
 IP Logged IP Logged |
Regards,
Michael Dagg
|
|
|
Marvin
Newbie


Gender: 
Posts: 5
|
 |
Re: 0.999...
« Reply #101 on: Dec 16th, 2006, 7:03am » |
 Quote Quote  Modify Modify
|
Yup, I was wrong, they don't contradict  Michael_Dagg wrote the representation of the number and Eigenray showed that such a number does not exist. Both correct. It was only confusing for A-man, I think. Michael_Dagg wrote the representation of the number and Eigenray showed that such a number does not exist. Both correct. It was only confusing for A-man, I think.
|
|
 IP Logged IP Logged |
|
|
|
rmsgrey
Uberpuzzler
    

    
Gender: 
Posts: 2874
|
 |
Re: 0.999...
« Reply #102 on: Dec 16th, 2006, 12:50pm » |
 Quote Quote  Modify Modify
|
Of course
Sup{x: x<1}
does exist and is 0.999...
(the supremum of a subset being its least upper bound within the parent set)
|
| « Last Edit: Dec 16th, 2006, 12:51pm by rmsgrey » |
 IP Logged IP Logged |
|
|
|
Michael Dagg
Senior Riddler
   

Gender: 
Posts: 500
|
 |
Re: 0.999...
« Reply #103 on: Dec 16th, 2006, 3:47pm » |
 Quote Quote  Modify Modify
|
sup{x: x < 1) exists and is
1 = sup{x: x< 1}.
You need max so-to-speak in this context. This idea is about
context if you ask me.
You can say that there is no largest number less than 1 by
using a set of no elements or some set upon which you assert
some kind of metric that does not exist.
Makes more sense to say max{x: x < 1} than say
something like {x: x = 1/0} or something like that. But, my choice one of many.
Anything wrong with this
sqrt(2) = sup{x in Q: x^2 < 2}.
The sqrt(2) is not even is in that set.
|
| « Last Edit: Dec 16th, 2006, 4:32pm by Michael Dagg » |
 IP Logged IP Logged |
Regards,
Michael Dagg
|
|
|
Marvin
Newbie


Gender: 
Posts: 5
|
 |
Re: 0.999...
« Reply #104 on: Dec 17th, 2006, 5:45am » |
 Quote Quote  Modify Modify
|
This gave me an idea of a proof that 0.999... = 1
Let S={x: x<1}. We will show that 0.999...=sup(S).
We need to show that 0.999...>=x for all x from S
Let epsilon = 10^-n, for an arbitrary natural n
x= 1 - epsilon = 0.99..(n-times)..9 < 0.999...
Now we want to show that for any epsilon>0, there is x in S such that x > 0.999... - epsilon.
We will use the same epsilon...
0.999... - epsilon = 0.99..(n-1-times)..9899... < 0.99..(n-times)..9 which lies in S (it is < 1)
It is obvious that sup(S)=1 :
1 is greater than any x from S trivially (it results from the definition of S)
1 - epsilon = 0.99..(n-times)..9 < 0.99..(n+1-times)..9 which lies in S ( it is < 1)
From the uniqueness of a supremum: 0.999... = 1

I hope I was formally correct...
|
|
 IP Logged IP Logged |
|
|
|
CowsRUs
Full Member
  

Why is it that cats are better then cows? Why not?
Gender: 
Posts: 175
|
 |
Re: 0.999...
« Reply #105 on: Feb 5th, 2007, 7:10pm » |
 Quote Quote  Modify Modify
|
well i may be contradicting Icarus, and i may be repeating sum1 else i dont know at all... Icarus [smiley...] sort of lost me there...
but i think he said this was true or not true
1.000...01 because if it was true then this whole argument is a waste:
.99999.... *10= .999999.....90- .999999... would equal 8.99999999.....91
u get my point?
as for the fractions 1/3 is not equal to .333... meaning. .333..... is short by a tiny bit to 1/3 unless u mean .333... as really 1/3 then 3(.333...) would equal 1
i may be repeating as i said but who really reads through 5 pages of stuff anywayz?
|
|
 IP Logged IP Logged |
"It is very good to have a brother who has a cow. It is also good to have a brother who has two cows. In fact, a brother with a cow is great, except when he has exactly 135 cows and is one of thecow himself."-Unknown
|
|
|
CowsRUs
Full Member
  

Why is it that cats are better then cows? Why not?
Gender: 
Posts: 175
|
 |
Re: 0.999...
« Reply #106 on: Feb 5th, 2007, 7:41pm » |
 Quote Quote  Modify Modify
|
Omg, the subject field wasnt filled out so i have to retype everything... im going to try to summarize it
if there are numbers after infinitives then there can be infinitives after infinitives(why not) if u add .999... to 1 and divide that by two. then u would get .999...945, and then u would do that infinitive times, therefore making it .999...999... infinitively*infinitively FOREVER. .999...999...999... for ... times. thats why infinitives are difficult to work with...
im probably wrong so explain to me why there cannot be numbers after an infinitive because however infinitively small it is, it will be still the difference between a difference of infinitively smallness. That is if we could be infinitively small then if we stand by an infinitively small-marked ruler than we would see the difference between .9999999...91 and .999...92
Prove me wrong...
that also brings me to the meaning of forever, and now that word confuses me since it involves an infinitive...   
|
|
 IP Logged IP Logged |
"It is very good to have a brother who has a cow. It is also good to have a brother who has two cows. In fact, a brother with a cow is great, except when he has exactly 135 cows and is one of thecow himself."-Unknown
|
|
|
Whiskey Tango Foxtrot
Uberpuzzler
    

Sorry Goose, it's time to buzz a tower.

Gender: 
Posts: 1672
|
 |
Re: 0.999...
« Reply #107 on: Feb 5th, 2007, 8:03pm » |
 Quote Quote  Modify Modify
|
Unknown. Firstly, we are not discussing grammar, so infinitives are definitely out. Please don't bring them up again.
Secondly, you demanded that we prove you wrong. Fortunately, several have already done so for us. If you had read the above posts, you would see that you have made something of a classic mistake in your reasoning. To summarize it, 0.999...995, were it to actually make any sense, would still be less than 0.999...
I am infinitively upset by your post 
|
| « Last Edit: Feb 5th, 2007, 8:26pm by Whiskey Tango Foxtrot » |
 IP Logged IP Logged |
"I do not feel obliged to believe that the same God who has endowed us with sense, reason, and intellect has intended us to forgo their use." - Galileo Galilei
|
|
|
BNC
Uberpuzzler
    

Gender: 
Posts: 1732
|
 |
Re: 0.999...
« Reply #108 on: Feb 6th, 2007, 12:23am » |
 Quote Quote  Modify Modify
|
on Feb 5th, 2007, 7:10pm, UNKNOWN wrote:| <snip> who really reads through 5 pages of stuff anywayz? |
|
People who want to understand?
People who want to avoid repeating common errors?
People who respect other people's time and effort in posting those 5 pages?
Short answer: number like 0.999....91 are meaningless. You never "reach" the last spot to write the "1".
PS: Contradicting Icarus is neer wise. And <a-hmm> infinitively more so at math-related issues.
|
|
 IP Logged IP Logged |
How about supercalifragilisticexpialidociouspuzzler [Towr, 2007]
|
|
|
Three Hands
Uberpuzzler
    


Gender: 
Posts: 715
|
 |
Re: 0.999...
« Reply #109 on: Feb 6th, 2007, 1:37am » |
 Quote Quote  Modify Modify
|
on Feb 5th, 2007, 7:10pm, UNKNOWN wrote:
i may be repeating as i said but who really reads through 5 pages of stuff anywayz? |
|
As one who made a similar argument towards the bottom of page one (I was young and foolish then...), I suggest you look at the top of page 2 for a suitable response...
(Granted, this is repeating much of what others have already said, but much of this topic has ended up repeating what others have said...)
|
|
 IP Logged IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
    

Boldly going where even angels fear to tread.
Gender: 
Posts: 4863
|
 |
Re: 0.999...
« Reply #110 on: Feb 6th, 2007, 6:27pm » |
 Quote Quote  Modify Modify
|
Unknown - I am sorry for the somewhat hostile reception, but it really is hard to keep your temper when you have to read through a badly written post several times trying to make any sense out of it. While spelling and grammar mistakes happen, it really is a good idea to make an attempt at clear communication.
As for the issue. It is possible to define notations such as 0.999...95 etc (where here the ... are meant to represent an infinite number of digits). However, simply having such notations does NOT mean they are actual real numbers. The real numbers are NOT decimal notations. They have an existence entirely apart from how we write them down. They are completely and uniquely determined by certain properties they possess. In particular, the real numbers are the minimal topologically complete ordered field (a phrase I defined in that first post - though it is now unreadable unless you use the tricks described in towr's post here).
Decimal notation is not how we define Real numbers. It is simply a scheme for naming them. In ordinary decimal notation, there are NO decimal digits in infinite positions. Every digit has only a finite number of digits to its left (and an infinite number to its right - terminating decimals are those for which the infinite number of digits are all 0) . There is no need for digits in infinite positions, as the ordinary decimal notation yields enough names so that every real number has one. In fact - as this riddle shows - some real numbers actually have two names!
If you decide to introduce decimal notations with with an infinite number of digits to the left of some digits, you are quite free to do so. But there is a caveat: You have to figure out what numbers they are supposed to represent. You need to define which number is to be represented by our new notation. This requires assigning even more names to our already named real numbers, or else introducing a new set of numbers to be represented by your new notations. In either case, your result does not in any gainsay 0.999... = 1, since these are already defined by ordinary decimal notation to be ordinary real numbers, and in that system, the two notations in fact represent the same number.
In order to understand the arguments you have referenced, you have to understand decimal notation. Of course, once you actually understand what infinite decimals mean, this whole problem becomes a no-brainer. Let's look at 0.999.... The definition of this expression is:
0.999... = 9/10 + 9/102 + 9/103 + ...
Now the question comes up: How do you sum up an infinite number of terms? The answer is, you can't. We have to find a means of defining the value that doesn't require that we actually add an infinite number of times. The means of doing this has been known since the time of the Greeks. We can't add up an infinite number of terms, but we can show that there is exactly one number x with the following properties:
(1) No matter how many terms of the sum we add up, the total will always be 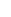 x. x.
(2) For any real number y < x, we can always add up enough of the terms to get a total > y.
We define the value of the infinite sum to the unique x for which this is true. That value is then also the real number named by the decimal expression. (How do we know the number is unique? That is built into the properties: if z is a second number with the same properties, then either z < x or x < z. But if z < x, then property (1) for z contradicts property (2) for x, and vice versa if x < z. Hence there can be only one number which satisfies both properties).
Now let's try to compare 1 to 0.999.... Summing up any finite number of terms is going to give you a number 0.999---9 (where I am using --- to represent a finite number of additional 9s). The meaning of this finite decimal notation is clear to everyone, I hope. The difference between 0.999---9 and 1 is 0.000---1 = 1/10n for some value of n. By choosing enough terms, I can make this expression as small as I like. In particular, if y < 1, then 1-y > 0, and I can choose n large enough so that 1/10n < 1-y. Turning this around gives y < 1 - 1/10n = 0.999---9. So x=1 satisfies property (2). Since 0.999---9 < 1, regardless of how many 9 are there (remember, --- means only a finite number), x=1 also satisfies property (1).
So 1 is the unique number satisfying both property (1) and property (2) for the sum 9/10 + 9/102 + 9/103 + ... . By definition, it is the value of that sum. By definition as well, the value of that sum is the value of 0.999...
That is, 0.999... = 1.
You are mistaken as well in your claim that 0.333... is a little less than 1/3. By the definition, it is exactly 1/3.
|
|
 IP Logged IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
CowsRUs
Full Member
  

Why is it that cats are better then cows? Why not?
Gender: 
Posts: 175
|
 |
Re: 0.999...
« Reply #111 on: Feb 7th, 2007, 5:25pm » |
 Quote Quote  Modify Modify
|
you know whats weird? why this thread has 110 replies and only 189 views when smaller threads have less 
|
|
 IP Logged IP Logged |
"It is very good to have a brother who has a cow. It is also good to have a brother who has two cows. In fact, a brother with a cow is great, except when he has exactly 135 cows and is one of thecow himself."-Unknown
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
    

Boldly going where even angels fear to tread.
Gender: 
Posts: 4863
|
 |
Re: 0.999...
« Reply #112 on: Feb 7th, 2007, 6:25pm » |
 Quote Quote  Modify Modify
|
I would guess that the count was corrupted when the server crashed a couple months ago. They eventually recovered most of the data, but every so often we come across something that got lost. Worst perhaps was that Alien's membership disappeared and he had to start again as Iceman. At least William was able to restore his post count, so he didn't have to wait to become an uberpuzzler all over again.
|
|
 IP Logged IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
CowsRUs
Full Member
  

Why is it that cats are better then cows? Why not?
Gender: 
Posts: 175
|
 |
Re: 0.999...
« Reply #113 on: Feb 7th, 2007, 7:25pm » |
 Quote Quote  Modify Modify
|
Oh, I never knew that!
Dang Nabbit!!!
am i saying that correctly?
|
|
 IP Logged IP Logged |
"It is very good to have a brother who has a cow. It is also good to have a brother who has two cows. In fact, a brother with a cow is great, except when he has exactly 135 cows and is one of thecow himself."-Unknown
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
    

Boldly going where even angels fear to tread.
Gender: 
Posts: 4863
|
 |
Re: 0.999...
« Reply #114 on: Feb 8th, 2007, 4:31pm » |
 Quote Quote  Modify Modify
|
Gol Dang it!, its "Dag Nabbit!", ya crazy young whippersnapper!
|
|
 IP Logged IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
CowsRUs
Full Member
  

Why is it that cats are better then cows? Why not?
Gender: 
Posts: 175
|
 |
Re: 0.999...
« Reply #115 on: Feb 8th, 2007, 4:45pm » |
 Quote Quote  Modify Modify
|
Ima put you old Wheezers into your PLACE!!!   
|
|
 IP Logged IP Logged |
"It is very good to have a brother who has a cow. It is also good to have a brother who has two cows. In fact, a brother with a cow is great, except when he has exactly 135 cows and is one of thecow himself."-Unknown
|
|
|
WakeTFU
Newbie




Gender: 
Posts: 7
|
 |
Re: 0.999...
« Reply #116 on: Feb 10th, 2007, 5:44pm » |
 Quote Quote  Modify Modify
|
For them, to say that 0.999... = 1 is patently ridiculous, since they quite evidently look nothing alike. But in fact, decimal expressions are not the numbers themselves, but are names for those numbers. They are labels which we have attached to underlying ideas to allow us to easily discuss them. 0.999... and 1 are two different names we use for the same concept
Yeah..you contradict yourtself, in case no ones had pointed that out yet...If they are different names for the same thing then it's not rediculous to write .999...=1, because it does.
If they aren't equal I double dog dare you to subtract something from one to get .999...
(if they're different numbers you will ALWAYS beable to subtract from one to get the other, and you can't)
Your best guess would be .000...1 which, if you understand the way infinity works, that number doesn't exist. Not in any usable form at least. THat number is entirely useless when doing math (except in this case, LOL) because it's just a zero.
.999...=1
|
|
 IP Logged IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
    

Boldly going where even angels fear to tread.
Gender: 
Posts: 4863
|
 |
Re: 0.999...
« Reply #117 on: Feb 11th, 2007, 12:19pm » |
 Quote Quote  Modify Modify
|
Would you please be so kind as to point out what I have ever said that contradicts that?
And if I somehow have contradicted myself, why are you arguing the same thing yourself?
|
|
 IP Logged IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
WakeTFU
Newbie




Gender: 
Posts: 7
|
 |
Re: 0.999...
« Reply #118 on: Feb 15th, 2007, 9:56pm » |
 Quote Quote  Modify Modify
|
" For them, to say that 0.999... = 1 is patently ridiculous"
-Icarus
No it isn't, is all I'm saying 
(ridiculous that is, it's not ridiculous)
heh, moving on...
You guys are all really smart...I hope your jobs make use of y'all...
|
|
 IP Logged IP Logged |
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 7527
|
 |
Re: 1
« Reply #119 on: Feb 16th, 2007, 5:08am » |
 Quote Quote  Modify Modify
|
Hey! why isn't this thread simply called "1"? 
|
|
 IP Logged IP Logged |
|
|
|
rmsgrey
Uberpuzzler
    

    
Gender: 
Posts: 2874
|
 |
Re: 1
« Reply #120 on: Feb 16th, 2007, 10:59am » |
 Quote Quote  Modify Modify
|
on Feb 16th, 2007, 5:08am, Grimbal wrote:Hey! why isn't this thread simply called "1"?  |
|
Notational convention 
|
|
 IP Logged IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
    

Boldly going where even angels fear to tread.
Gender: 
Posts: 4863
|
 |
Re: 0.999...
« Reply #121 on: Feb 16th, 2007, 4:41pm » |
 Quote Quote  Modify Modify
|
on Feb 15th, 2007, 9:56pm, WakeTFU wrote:" For them, to say that 0.999... = 1 is patently ridiculous"
-Icarus
No it isn't, is all I'm saying  |
|
You know, if you take something completely out of its context, then you really cannot expect it to make sense.
Why don't we just look at this quote where it belongs:
on May 1st, 2004, 7:19pm, Icarus wrote:| One of the problems that people have with the question of the meaning of 0.999... is a misunderstanding of what real numbers themselves are. In particular, many mistake the decimal expressions we write out as being the numbers themselves. For them, to say that 0.999... = 1 is patently ridiculous, since they quite evidently look nothing alike. But in fact, decimal expressions are not the numbers themselves, but are names for those numbers. They are labels which we have attached to underlying ideas to allow us to easily discuss them. 0.999... and 1 are two different names we use for the same concept. |
|
If you will read that carefully this time, you will notice that I am describing a misconception that is the main cause of people having trouble with this. I never said myself that 0.999... = 1 is ridiculous. Instead I am pointing out that people who have this misconception believe that it is.
Then I immediately point out what that misconception is!
There is no contradiction in this.
|
|
 IP Logged IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
    

Boldly going where even angels fear to tread.
Gender: 
Posts: 4863
|
 |
Re: 0.999...
« Reply #122 on: Feb 16th, 2007, 8:16pm » |
 Quote Quote  Modify Modify
|
Thought I'd play around with SMQ's new math symbols tool, and give a short intro to surreal numbers (a concept I'm fairly new to myself). Most of what is here is standard to the subject. A few aspects are my own interpretation (that is, I didn't get it from any other source - someone else may have done the same thing before me though). In particular, my sources defined surreal numbers with looser rules on the sets used, and as a result end up with many equivalent representations for the same number. The numbers themselves were defined as equivalence classes on the representations. But I saw that there was a "privileged" member in each class, and it made more sense to me to define the surreal number to be this member.
Surreal Numbers
Surreal numbers are amongst those "collections" that cannot be held within an ordinary set without introducing contradictions (cardinal numbers and ordinal numbers likewise suffer this problem). So instead of defining a set that defines all of them, we must define them in smaller increments. The standard method is to define them inductively using an ever increasing collection of sets. If we are going to use induction, then we need a well ordered collection to induct on. For this, we choose the ordinals (which is why the surreals require Russell-Whitehead collections rather than Zermelo-Frankel sets).
This may seem like cheating, since the ordinals already have 0,1,2,... defined, and we are going to want to get these same numbers out of our Surreal construction. However, for our purposes the only property of the ordinals needed is the order. So we don't actually think of ordinal 0,1,2,... etc as numbers.
To build the Surreal numbers, we need the Cut operator: { ... | ... }. If S is a totally ordered set, a cut of S is a pair of subsets A,B of S such that:
(i) A  B = S B = S
(ii) A  B = B = 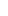
(iii) for all a  A and b A and b  B, a < b. B, a < b.
If A, B are a cut of S, define {A|B} to be the pair (A, B).
A common notational convention used in Surreal numbers is to replace the sets A and B with lists of their members: {a1, a2, ... | b1, b2, ...}. So, for instance {0,1 | 2,3} would represent the pair ({0,1},{2,3}).
(*) We start with the empty set 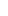 as our un-indexed base. as our un-indexed base.
(0) Next we define 0 = {|} and define the set S0 = {0}.
(1) S0 has exactly 2 cuts: Define -1 = {|0}, 1 = {0|}. Define S1 = {-1, 0, 1}.
(2) S1 has 4 cuts: -2 = {|-1,0,1}, -1/2 = {-1|0,1}, 1/2 = {-1,0|1}, 2 = {-1,0,1|}. Define S2 = {-2, -1, -1/2, 0, 1/2, 1, 2}.
...
Suppose that S has been defined for all has been defined for all 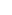 < < 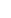 for some ordinal for some ordinal 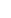 , such that if , such that if 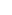 < < 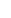 < < 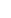 , then S , then S 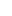 S S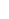 . Further suppose that all the S . Further suppose that all the S are ordered with compatible orders (that is if x, y are ordered with compatible orders (that is if x, y  S S 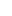 S S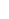 , and x < y in S , and x < y in S , then x < y in S , then x < y in S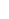 as well). as well).
Define O =   S S . O is ordered by the common ordering inherited from the S . O is ordered by the common ordering inherited from the S . This ordering determines cuts in O. Define N = { {A|B} : {A|B} is a cut of O}, and define S . This ordering determines cuts in O. Define N = { {A|B} : {A|B} is a cut of O}, and define S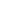 = O = O  N. N.
We must still define the ordering on S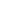 . If x,y are in O, then we inherit the ordering of O. If x . If x,y are in O, then we inherit the ordering of O. If x  O and y O and y  N, Let y = {C|D}. Since y is a cut of O, x N, Let y = {C|D}. Since y is a cut of O, x  C or x C or x  D. If x D. If x  C, define x < y. If x C, define x < y. If x  D, we define y < x. Lastly, if x, y D, we define y < x. Lastly, if x, y  N, then x = {A|B} and y = {C|D}. By the nature of cuts, either A N, then x = {A|B} and y = {C|D}. By the nature of cuts, either A 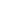 C or C C or C 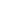 A. In the former case, define x A. In the former case, define x  y, and in the latter case, y y, and in the latter case, y  x. x.
This completes the induction.
|
|
 IP Logged IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
    

Boldly going where even angels fear to tread.
Gender: 
Posts: 4863
|
 |
Re: 0.999...
« Reply #123 on: Feb 16th, 2007, 9:00pm » |
 Quote Quote  Modify Modify
|
Continuing...
Some comments:
(1) In addition to the normal ordering of numbers that develops with this, we also get another relationship: "age". Some numbers are introduced earlier in the process than others. The "birthday" of any particular surreal number x is the lowest ordinal 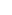 such that x such that x  S S . If the birthday of x is before the birthday of y, then x is said to be "older than" y. If they have the same birthday, then x is "the same age as" y. . If the birthday of x is before the birthday of y, then x is said to be "older than" y. If they have the same birthday, then x is "the same age as" y.
(2) The only numbers with finite birthdays are the integers and fractions of the form n/2m. The entire rest of the real numbers have  (the first infinite ordinal) as their birthday. (the first infinite ordinal) as their birthday.
(3) The age operator allows us to expand the definition of the cut operator: Define "A < B" to mean that for all a  A and b A and b  B, a < b. Then for any pair of sets A, B of surreal numbers, define {A|B} to be the oldest surreal number x such that for all a B, a < b. Then for any pair of sets A, B of surreal numbers, define {A|B} to be the oldest surreal number x such that for all a  A, b A, b  B, a < x < b (by the definition of surreal numbers, such an x must exist and is unique). B, a < x < b (by the definition of surreal numbers, such an x must exist and is unique).
(4) S is not is not 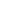 , however. If we define Sf = , however. If we define Sf =  n=0 n=0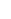 Sn, then some elements of S Sn, then some elements of S not in not in 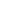 are: - are: -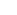 = {|Sf}, = {|Sf}, 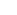 = {Sf|}. Also, consider the somewhat troublesome numbers {{x = {Sf|}. Also, consider the somewhat troublesome numbers {{x  0} | {x > 0} } and { {x < 1} | {x 0} | {x > 0} } and { {x < 1} | {x  1}}. That is, in S 1}}. That is, in S , there IS a smallest number greater than 0, and a largest number less than 1! (However, the surreals do not end with S , there IS a smallest number greater than 0, and a largest number less than 1! (However, the surreals do not end with S - the next iteration drops more numbers in between these.) - the next iteration drops more numbers in between these.)
No collection deserves the title "numbers", however, unless you can add and multiply them. For surreals, these are defined inductively:
On our base set 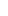 , both operators are defined "vacuously". , both operators are defined "vacuously".
If +, * have been defined for all surreals with birthday < 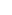 , let x, y , let x, y  S S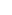 . Then x = {A|B}, y={C|D}. . Then x = {A|B}, y={C|D}. It is easy to see that A + C < B + D. Hence by (3) above we can define x + y = {A+C|B+D}. Unfortunately, the corresponding expression for multiplication is actually quite nasty (because A*C is not less than B*D, finding the right sets is much more complicated).
[edit]My "definition" for addition was written from a poor memory. It breaks down in certain instances. The official version is x + y = {x+C  y+A | x+D y+A | x+D  y+B}.[/edit] y+B}.[/edit]
|
| « Last Edit: Feb 25th, 2007, 7:57pm by Icarus » |
 IP Logged IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 2084
|
 |
Re: 0.999...
« Reply #124 on: Feb 17th, 2007, 5:16am » |
 Quote Quote  Modify Modify
|
What I think is "fun" is that under those definitions, expressions like 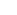 - 1, (technically - 1, (technically  - 1) and - 1) and  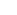 are meaningful and useful numbers! are meaningful and useful numbers!
Now here's a question I haven't found an answer to: the Wikipedia article states (witout proof, although I believe it to be correct) that where the reals are the "smallest topologically complete ordered field", the surreals are the largest ordered field (if we allow fields to be defined over proper classes/collections as well as sets); does that make the complex surreals (A + B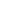 where A and B are surreal numbers and where A and B are surreal numbers and 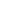 is defined to be is defined to be  -1 as usual) the largest algebraicly closed field? I.e. can all algebraically closed fields be embedded in the complex surreals? -1 as usual) the largest algebraicly closed field? I.e. can all algebraically closed fields be embedded in the complex surreals?
And does 0.999... still equal 1? 
--SMQ
|
|
 IP Logged IP Logged |
--SMQ
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register