 Author
Author |
Topic: Radicals (Read 867 times) |
|
ThudnBlunder
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
Find all positive numbers a such that 3 (3 + (3 +  a) + 3 a) + 3 (3 - (3 -  a) is an integer. a) is an integer.
|
| « Last Edit: Apr 2nd, 2007, 1:52am by ThudnBlunder » |
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
Barukh
Uberpuzzler
    

Gender: 
Posts: 2276
|
 |
Re: Radicals
« Reply #1 on: Apr 2nd, 2007, 3:14am » |
 Quote Quote  Modify Modify
|
Should a be an integer?
|
|
 IP Logged IP Logged |
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 7528
|
 |
Re: Radicals
« Reply #2 on: Apr 2nd, 2007, 4:59am » |
 Quote Quote  Modify Modify
|
That would leave only the numbers 0 to 9 to try. I would say any number.
"Positive" suggests a can not be complex. So any positive real number.
There might be extra solutions if the result can be any Gaussian integer.
|
|
 IP Logged IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: Radicals
« Reply #3 on: Apr 2nd, 2007, 7:41am » |
 Quote Quote  Modify Modify
|
Isn't the answer all positive numbers? Like last time?
For some integer x, and some y we have [x+ sqrt(y)]3=3+sqrt(a) and [x - sqrt(y)]3=3-sqrt(a)
x+ sqrt(y) + x - sqrt(y) = 2 x
|
| « Last Edit: Apr 2nd, 2007, 7:43am by towr » |
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 7528
|
 |
Re: Radicals
« Reply #4 on: Apr 2nd, 2007, 10:03am » |
 Quote Quote  Modify Modify
|
I don't think you can always find such x and y.
Consider a=0.
3 (3+ (3+ a) + 3 a) + 3 (3- (3- a) = 2·3 a) = 2·3 3 and it is not an integer. 3 and it is not an integer.
|
|
 IP Logged IP Logged |
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 2084
|
 |
Re: Radicals
« Reply #5 on: Apr 2nd, 2007, 11:57am » |
 Quote Quote  Modify Modify
|
In fact, since a = 0 gives a value of 23 3 3 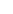 2.88, and the function is monotonic decreasing and always positive, the only integer values it can have are 2 and 1 at the corresponding values of a, right? 2.88, and the function is monotonic decreasing and always positive, the only integer values it can have are 2 and 1 at the corresponding values of a, right?
--SMQ
|
|
 IP Logged IP Logged |
--SMQ
|
|
|
Barukh
Uberpuzzler
    

Gender: 
Posts: 2276
|
 |
Re: Radicals
« Reply #6 on: Apr 2nd, 2007, 12:06pm » |
 Quote Quote  Modify Modify
|
SMQ, I think you are right.
The problem is to find an expression (I think in radicals) for such a.
|
|
 IP Logged IP Logged |
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 2084
|
 |
Re: Radicals
« Reply #7 on: Apr 2nd, 2007, 12:24pm » |
 Quote Quote  Modify Modify
|
For x = 3 (3 + (3 +  a) + 3 a) + 3 (3 - (3 -  a), I get a = 9 - (x3 - 6)3/(3x)3, which gives a = 242/27 at x = 2 and a = 368/27 at x = 1. a), I get a = 9 - (x3 - 6)3/(3x)3, which gives a = 242/27 at x = 2 and a = 368/27 at x = 1.
Edit -- derivation:
(1) x = 3 (3 + (3 +  a) + 3 a) + 3 (3 - (3 -  a) a)
(2) x3 = 6 + 3 3 3 ((3 + ((3 +  a)2(3 - a)2(3 -  a) + 3 a) + 3 3 3 ((3 + ((3 +  a)(3 - a)(3 -  a)2) a)2)
(3) (x3 - 6)/3 = 3 ((3 + ((3 +  a)2(3 - a)2(3 -  a) + 3 a) + 3 ((3 + ((3 +  a)(3 - a)(3 -  a)2) a)2)
(4) ((x3 - 6)/3)3 = (3 +  a)2(3 - a)2(3 -  a) + 3 a) + 3 3((3 + 3((3 +  a)5(3 - a)5(3 -  a)4) + 3 a)4) + 3 3 3 ((3 + ((3 +  a)4(3 - a)4(3 -  a)5) + (3 + a)5) + (3 +  a)(3 - a)(3 -  a)2 a)2
(5) ((x3 - 6)/3)3 = (3 +  a)(3 - a)(3 -  a)[6 + 3 a)[6 + 3 3 3 ((3 + ((3 +  a)2(3 - a)2(3 -  a) + 3 a) + 3 3 3 ((3 + ((3 +  a)(3 - a)(3 -  a)2)] a)2)]
(6) ((x3 - 6)/3)3 = (9 - a)[x3] (substituting from (2) for the bracketed term)
(7) 9 - a = ((x3 - 6)/(3x))3
--SMQ
|
| « Last Edit: Apr 2nd, 2007, 1:29pm by SMQ » |
 IP Logged IP Logged |
--SMQ
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: Radicals
« Reply #8 on: Apr 2nd, 2007, 4:31pm » |
 Quote Quote  Modify Modify
|
There's a simpler (or at least easier to read) derivation:
If x = u + v, then
x3 = u3 + v3 + 3uv x.
Substituting then, we have
x3 = 6 + 3(9-a)1/3 x,
which is easily solved for a.
|
|
 IP Logged IP Logged |
|
|
|
Barukh
Uberpuzzler
    

Gender: 
Posts: 2276
|
 |
Re: Radicals
« Reply #9 on: Apr 4th, 2007, 5:52am » |
 Quote Quote  Modify Modify
|

How about this variation: 3 (3 + (3 +  a) - 3 a) - 3 (3 - (3 -  a) is an integer, and a is a rational? a) is an integer, and a is a rational?
|
|
 IP Logged IP Logged |
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 2084
|
 |
Re: Radicals
« Reply #10 on: Apr 4th, 2007, 6:39am » |
 Quote Quote  Modify Modify
|
By Eigenray's derivation, x = u - v 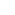 x3 = u3 - v3 - 3uvx x3 = u3 - v3 - 3uvx 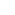 a = 9 - (6 - x3)/(3x)[/sup]3[/sup] so a is rational (and positive) for all integer x a = 9 - (6 - x3)/(3x)[/sup]3[/sup] so a is rational (and positive) for all integer x  0. 0.
Edit: erm, not quite, as Barukh points out below. See, this is why I'm a computer programmer and not a mathematician ... other programmers find my off-the-cuff answers convincing. 
--SMQ
|
| « Last Edit: Apr 4th, 2007, 10:59am by SMQ » |
 IP Logged IP Logged |
--SMQ
|
|
|
Barukh
Uberpuzzler
    

Gender: 
Posts: 2276
|
 |
Re: Radicals
« Reply #11 on: Apr 4th, 2007, 10:49am » |
 Quote Quote  Modify Modify
|
on Apr 4th, 2007, 6:39am, SMQ wrote:x = u - v 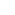 x3 = u3 - v3 - 3uvx[/hide]. x3 = u3 - v3 - 3uvx[/hide]. |
|
What's the value of u3 - v3?
|
|
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register