 Author
Author |
Topic: Complex roots (Read 2197 times) |
|
Sameer
Uberpuzzler
    

Pie = pi * e
Gender: 
Posts: 1261
|
 |
Complex roots
« on: Sep 17th, 2007, 11:21pm » |
 Quote Quote  Modify Modify
|
Another one from my book:
Find all the roots of the equation: (x - 1)n = xn where n is a positive integer.
|
| « Last Edit: Sep 17th, 2007, 11:22pm by Sameer » |
 IP Logged IP Logged |
"Obvious" is the most dangerous word in mathematics.
--Bell, Eric Temple
Proof is an idol before which the mathematician tortures himself.
Sir Arthur Eddington, quoted in Bridges to Infinity
|
|
|
Aryabhatta
Uberpuzzler
    

Gender: 
Posts: 1321
|
 |
Re: Complex roots
« Reply #1 on: Sep 18th, 2007, 1:33am » |
 Quote Quote  Modify Modify
|
Clearly x = 0 is not a root.
Divide by xn and we are done, right?
|
|
 IP Logged IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: Complex roots
« Reply #2 on: Sep 18th, 2007, 9:44am » |
 Quote Quote  Modify Modify
|
So x = 1/(1- r), where r is any of the nth roots of 1.
i.e., if memory serves me right, r= ei 2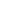 k/n with k=0..n-1 k/n with k=0..n-1
|
| « Last Edit: Sep 18th, 2007, 9:46am by towr » |
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
pex
Uberpuzzler
    

Gender: 
Posts: 880
|
 |
Re: Complex roots
« Reply #3 on: Sep 18th, 2007, 2:02pm » |
 Quote Quote  Modify Modify
|
on Sep 18th, 2007, 9:44am, towr wrote:So x = 1/(1- r), where r is any of the nth roots of 1.
i.e., if memory serves me right, r= ei 2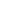 k/n with k=0..n-1 k/n with k=0..n-1
|
|
Yes, except that k=0 won't work, obviously.
|
|
 IP Logged IP Logged |
|
|
|
Sameer
Uberpuzzler
    

Pie = pi * e
Gender: 
Posts: 1261
|
 |
Re: Complex roots
« Reply #4 on: Sep 18th, 2007, 9:46pm » |
 Quote Quote  Modify Modify
|
on Sep 18th, 2007, 1:33am, Aryabhatta wrote:Clearly x = 0 is not a root.
Divide by xn and we are done, right? |
|
Yep.
on Sep 18th, 2007, 2:02pm, pex wrote:
Yes, except that k=0 won't work, obviously. |
|
Well in this case k = 0 does work!! (I think!!!)
|
|
 IP Logged IP Logged |
"Obvious" is the most dangerous word in mathematics.
--Bell, Eric Temple
Proof is an idol before which the mathematician tortures himself.
Sir Arthur Eddington, quoted in Bridges to Infinity
|
|
|
Aryabhatta
Uberpuzzler
    

Gender: 
Posts: 1321
|
 |
Re: Complex roots
« Reply #5 on: Sep 18th, 2007, 11:40pm » |
 Quote Quote  Modify Modify
|
on Sep 18th, 2007, 9:46pm, Sameer wrote:
Yep.
Well in this case k = 0 does work!! (I think!!!) |
|
The original equation has exactly n-1 roots (counting multiplicity) as it is a polynomial of degree n-1.
So we have to reject one root.
|
|
 IP Logged IP Logged |
|
|
|
pex
Uberpuzzler
    

Gender: 
Posts: 880
|
 |
Re: Complex roots
« Reply #6 on: Sep 19th, 2007, 5:40am » |
 Quote Quote  Modify Modify
|
on Sep 18th, 2007, 11:40pm, Aryabhatta wrote:
The original equation has exactly n-1 roots (counting multiplicity) as it is a polynomial of degree n-1.
So we have to reject one root. |
|
Yes, and k = 0 leads to r = 1, leaving x = 1/(1 - r) undefined.
|
|
 IP Logged IP Logged |
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 7527
|
 |
Re: Complex roots
« Reply #7 on: Sep 19th, 2007, 5:52am » |
 Quote Quote  Modify Modify
|
Now compute Re(x)
|
|
 IP Logged IP Logged |
|
|
|
pex
Uberpuzzler
    

Gender: 
Posts: 880
|
 |
Re: Complex roots
« Reply #8 on: Sep 19th, 2007, 6:12am » |
 Quote Quote  Modify Modify
|
on Sep 19th, 2007, 5:52am, Grimbal wrote:That's interesting! I get that Re(x) = 1/2 for all of the roots. Derivation:| hidden: | xk = 1 / (1 - exp(2k pi i / n))
= (1 - exp(-2k pi i / n)) / (2 - exp(2k pi i / n) - exp(-2k pi i / n))
= (1 - cos(2k pi / n) + i sin(2k pi / n)) / (2 - 2cos(2k pi / n))
= 1/2 + 1/2 i [ sin(2k pi / n) / (1 - cos(2k pi / n)) ],
and clearly, the real part is 1/2, independent of k. |
|
| « Last Edit: Sep 19th, 2007, 6:13am by pex » |
 IP Logged IP Logged |
|
|
|
Sameer
Uberpuzzler
    

Pie = pi * e
Gender: 
Posts: 1261
|
 |
Re: Complex roots
« Reply #9 on: Sep 19th, 2007, 9:18am » |
 Quote Quote  Modify Modify
|
Yep, I just thought infinity could be one of the roots!! Maybe not.. Yep I get the real part to be 1/2 too!! My original answer was in a reduced form 1/2(1+icotk /2) k=1..n-1 which easily showed what the real part was. /2) k=1..n-1 which easily showed what the real part was.
|
|
 IP Logged IP Logged |
"Obvious" is the most dangerous word in mathematics.
--Bell, Eric Temple
Proof is an idol before which the mathematician tortures himself.
Sir Arthur Eddington, quoted in Bridges to Infinity
|
|
|
srn437
Newbie


the dark lord rises again....
Posts: 1
|
 |
Re: Complex roots
« Reply #10 on: Sep 19th, 2007, 6:38pm » |
 Quote Quote  Modify Modify
|
If n is even, x can be 1/2.
|
|
 IP Logged IP Logged |
|
|
|
Sameer
Uberpuzzler
    

Pie = pi * e
Gender: 
Posts: 1261
|
 |
Re: Complex roots
« Reply #11 on: Sep 19th, 2007, 6:55pm » |
 Quote Quote  Modify Modify
|
on Sep 19th, 2007, 6:38pm, srn347 wrote:| If n is even, x can be 1/2. |
|
The question asks for general solution over all n.
|
|
 IP Logged IP Logged |
"Obvious" is the most dangerous word in mathematics.
--Bell, Eric Temple
Proof is an idol before which the mathematician tortures himself.
Sir Arthur Eddington, quoted in Bridges to Infinity
|
|
|
srn437
Newbie


the dark lord rises again....
Posts: 1
|
 |
Re: Complex roots
« Reply #12 on: Sep 23rd, 2007, 3:29pm » |
 Quote Quote  Modify Modify
|
It wuold have to be one where x=x-1, so x=infinity.
|
|
 IP Logged IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: Complex roots
« Reply #13 on: Sep 23rd, 2007, 11:16pm » |
 Quote Quote  Modify Modify
|
on Sep 23rd, 2007, 3:29pm, srn347 wrote:| It wuold have to be one where x=x-1, so x=infinity. |
|
And yet again you fail.
There are n-1 solutions that don't tend to infinity. And since infinity isn't a complex number it can't be a solution, so only those other n-1 remain.
|
|
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
srn437
Newbie


the dark lord rises again....
Posts: 1
|
 |
Re: Complex roots
« Reply #14 on: Sep 24th, 2007, 6:25pm » |
 Quote Quote  Modify Modify
|
It has to be complex? Take the n root and x=x-1, therefore it must be infinity(positive or negative).
|
|
 IP Logged IP Logged |
|
|
|
Sameer
Uberpuzzler
    

Pie = pi * e
Gender: 
Posts: 1261
|
 |
Re: Complex roots
« Reply #15 on: Sep 24th, 2007, 8:24pm » |
 Quote Quote  Modify Modify
|
on Sep 24th, 2007, 6:25pm, srn347 wrote:| It has to be complex? Take the n root and x=x-1, therefore it must be infinity(positive or negative). |
|
ok to make it easier to understand, if you have complex set available, what are all the roots of x3 = 1?
|
|
 IP Logged IP Logged |
"Obvious" is the most dangerous word in mathematics.
--Bell, Eric Temple
Proof is an idol before which the mathematician tortures himself.
Sir Arthur Eddington, quoted in Bridges to Infinity
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: Complex roots
« Reply #16 on: Sep 25th, 2007, 1:26am » |
 Quote Quote  Modify Modify
|
on Sep 24th, 2007, 6:25pm, srn347 wrote:Complex numbers include the real numbers, FYI. Infinity is neither a real number, nor an imaginary number nor a combination. Hence it can't be a solution.
Quote:| Take the n root and x=x-1, therefore it must be infinity(positive or negative). |
|
Wrong. By simply taking the nth root at both sides, you lose n-1 solutions (and there are only n-1 solutions in the first place)
If e.g. x2=(x-1)2, then you don't get the solution by taking x=(x-1); so why would you think this is allowed for other n?
For x2=(x-1)2, just simplify the equation:
(x-1)2 = x2 -2x + 1, therefore x2=x2 -2x + 1, or x=1/2.
You even suggested x=1/2 yourself for even n!
|
| « Last Edit: Sep 25th, 2007, 1:26am by towr » |
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
srn437
Newbie


the dark lord rises again....
Posts: 1
|
 |
Re: Complex roots
« Reply #17 on: Sep 25th, 2007, 5:07pm » |
 Quote Quote  Modify Modify
|
The roots of x3=1 are 1, -1/2 + sqrt(3)(i)/2, and -1/2 -sqrt(3)(i)/2
|
|
 IP Logged IP Logged |
|
|
|
Sameer
Uberpuzzler
    

Pie = pi * e
Gender: 
Posts: 1261
|
 |
Re: Complex roots
« Reply #18 on: Sep 25th, 2007, 6:12pm » |
 Quote Quote  Modify Modify
|
on Sep 25th, 2007, 5:07pm, srn347 wrote:| The roots of x3=1 are 1, -1/2 + sqrt(3)(i)/2, and -1/2 -sqrt(3)(i)/2 |
|
Good, now look at towr's example and what do you learn?
|
|
 IP Logged IP Logged |
"Obvious" is the most dangerous word in mathematics.
--Bell, Eric Temple
Proof is an idol before which the mathematician tortures himself.
Sir Arthur Eddington, quoted in Bridges to Infinity
|
|
|
srn437
Newbie


the dark lord rises again....
Posts: 1
|
 |
Re: Complex roots
« Reply #19 on: Sep 25th, 2007, 8:04pm » |
 Quote Quote  Modify Modify
|
That there are no real solutions for all natural number exponents(which I already new).
|
|
 IP Logged IP Logged |
|
|
|
Obob
Senior Riddler
   

Gender: 
Posts: 489
|
 |
Re: Complex roots
« Reply #20 on: Sep 25th, 2007, 8:30pm » |
 Quote Quote  Modify Modify
|
Except whenever n is even, x=1/2 is a solution...
|
|
 IP Logged IP Logged |
|
|
|
Sameer
Uberpuzzler
    

Pie = pi * e
Gender: 
Posts: 1261
|
 |
Re: Complex roots
« Reply #21 on: Sep 25th, 2007, 8:44pm » |
 Quote Quote  Modify Modify
|
on Sep 25th, 2007, 8:04pm, srn347 wrote:| That there are no real solutions for all natural number exponents(which I already new). |
|
What part of the title of this problem confuses you? Are you genuinely trying to learn or just wasting my time?
|
|
 IP Logged IP Logged |
"Obvious" is the most dangerous word in mathematics.
--Bell, Eric Temple
Proof is an idol before which the mathematician tortures himself.
Sir Arthur Eddington, quoted in Bridges to Infinity
|
|
|
srn437
Newbie


the dark lord rises again....
Posts: 1
|
 |
Re: Complex roots
« Reply #22 on: Sep 26th, 2007, 7:23pm » |
 Quote Quote  Modify Modify
|
As already stated, you need to have all the n's answered. x would have to equal n-1.
|
|
 IP Logged IP Logged |
|
|
|
Sameer
Uberpuzzler
    

Pie = pi * e
Gender: 
Posts: 1261
|
 |
Re: Complex roots
« Reply #23 on: Sep 26th, 2007, 9:39pm » |
 Quote Quote  Modify Modify
|
Note to Mods: Can you please delete posts that are irrelevant to this thread? You get my drift!!
|
|
 IP Logged IP Logged |
"Obvious" is the most dangerous word in mathematics.
--Bell, Eric Temple
Proof is an idol before which the mathematician tortures himself.
Sir Arthur Eddington, quoted in Bridges to Infinity
|
|
|
srn437
Newbie


the dark lord rises again....
Posts: 1
|
 |
Re: Complex roots
« Reply #24 on: Sep 26th, 2007, 9:48pm » |
 Quote Quote  Modify Modify
|
Try asking a question with an answer!
|
|
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register